AP Statistics / Mr. Hansen 11/9/2004

Name: _________________________

Partial Answer Key to Test #1

Note: This answer key is provided in order to help you check a few of the answers from the September 1998 test. Some of the details are omitted here. Remember that you must show full work for full credit. In general, full work consists of formula, plug-ins, and answer (circled, with correct units such as dollars or years).

13.	explanatory variable: speed (mph) response variable: fine ($)
14.
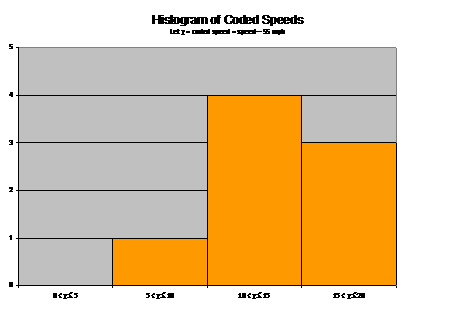
	Possible answers for the analysis question: § Although sample size is tiny, some left skewness is visible. § In the data set sampled, almost all tickets written were for at least 10 mph over the speed limit. § The distribution has no apparent gaps or outliers. § Many other answers are possible.
15.	7 = min. 10 = Q1 13.5 = median = Q2 16 = Q3 18 = max.
16.	s = 3.780 mph
17.	For the original data, s = 3.780 mph. There is no change, since s.d. is unaffected by a positive or negative shift (in this case, down 55). The s.d. changes only if the domain is contracted or dilated.
18.
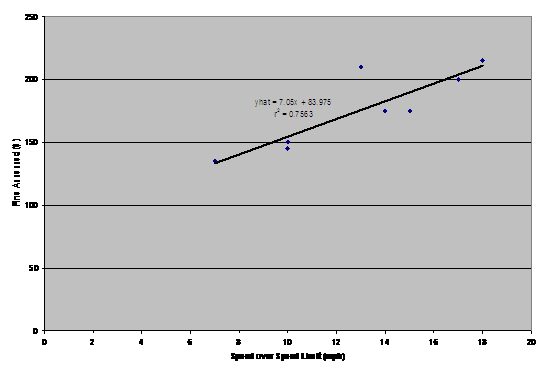
19.	b1 = slope = 7.050 dollars/mph
20.	Judge Jeremy is fairly predictable; there is a strong positive linear correlation (r = .870) between excess speed and the fine assessed.
21.	Note: 70 mph is coded as 70 – 55 = 15. yhat = b0 + b1x         = 83.975 + 7.050(15)         = $189.725 (round to $190 only if nearest dollar is requested)
22.	yhat = b0 + b1x         = 83.975 + 7.050(2)         = $98.075 (round to $98 only if nearest dollar is requested) However, this prediction is unreasonable because it involves extrapolation beyond the domain of known x values.
23.	regression outlier
24.	7.050 dollars/mph
25.	Answers will vary. Some people would say no, since there was very little change in the slope (in fact, no change, which is extremely unusual). Others would say yes, since the r value changed quite a bit, from .870 to .976. As long as you provide a sentence of explanation, you should be all right.
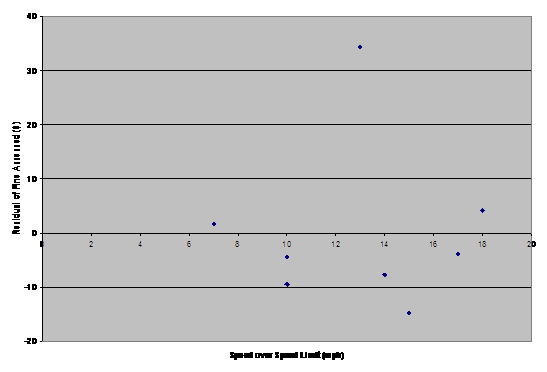
26.
	The sample is too small too support any obvious conclusions. The residual plot appears to be sufficiently random, at least for such a small data set.