1.(a) Fill in the blank. The Mean Value Theorem states that for any function f that is differentiable on (a, b) and continuous on [a, b] there exists at least one value c Î (a, b) such that
______________ .

(b) Fill in the blank. We say that f is ______________ at x = c iff f (c) exists and .

2.(a) Fill in the blank. If f is differentiable, we define the derivative at a point c to be

______________ .

(b) Use the definition of the derivative as a function to find and simplify when . (Yes, of course you know how to do this much more efficiently. The purpose of this problem is to see if you remember how to apply the definition of the derivative as a function.)

3.(a) Sketch a polynomial function f that does not have a point of inflection at x = 0 even though . (Hint: y = x³ does not work.) Define your function here: f (x) = ____________ .

(b) Let h be a continuous function on  . Is it possible for h to have two cusps, one of which is a point of inflection and one of which is not a point of inflection? (Circle one: Yes No )
Either sketch a function h that satisifies this condition, or explain why it cannot be true. If you do find such a function, write a short sentence on your graph that points to the first cusp and explains why it is a point of inflection. You need not define h algebraically.

4. Let .

(a) Use the derivative formula for to find . (Hint: You may wish to use negative exponents to simplify the argument of the tangent function somewhat.)

(b) Use the trigonometric definition of the tangent in terms of sine and cosine, along with the quotient rule, to find . Simplify your answer enough to match your answer to part (a) as closely as possible.

5. Fill in the blanks. Each of the graphs below shows the position of a particle moving along the x-axis as a function of time, . The vertical scales of the graphs are the same. During this time interval, which particle has

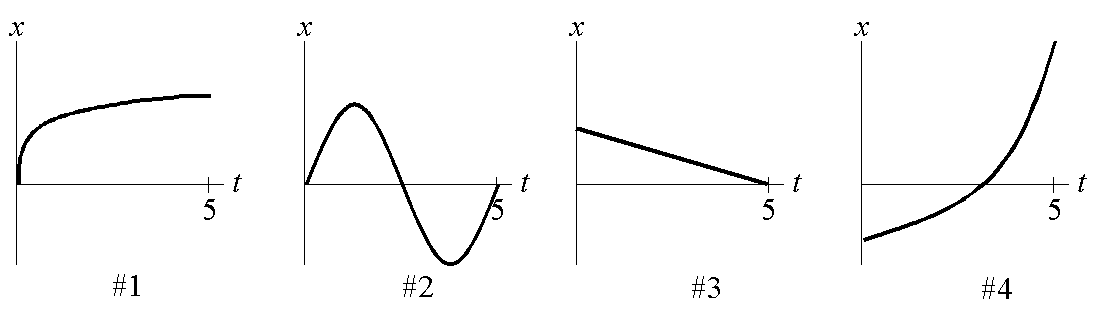
6. Consider the function .

(a) Use upper Riemann sums with 5 mesh points (i.e., 4 intervals) to estimate . Indicate whether this requires the (circle one) right endpoint or left endpoint method. Show all your work, preferably in a table.

(b) Use the fundamental theorem of calculus and techniques of antidifferentiation to find the exact algebraic value for . By how much did part (a) overestimate the true value?

(c) Use your calculator’s built-in numeric integration feature to find directly. What is your answer? _____________ Does this agree with part (b)? _____ . (No need to show work.)

7. Let .

(a) Sketch the slope field defined by this separable differential equation. On the same set of axes, sketch the particular solution that passes through the point (2.2, 6).

(b) Use Euler’s method (or the linear estimator, which is the same thing) to estimate y when x = 2.3, employing a single step of size 0.1. Show your work.

8.(a) Solve the differential equation given at the beginning of problem 7. (In other words, find the exact algebraic form of y.)

(b) If you were to run the EULER program, you would see that a starting point of x = 2.2 and a step size of 0.1 will give an estimated y value of 5.561156 when x = 2.5. (There is no need for you to verify this unless you are curious.) By how much is this estimated y value in error?

(c) State in a few words (or at most one sentence) why it is reasonable for Euler’s method to consistently underestimate y as we step to the right of x = 2.2.

9.(a) Without using your calculator (except perhaps as a check), compute .

(b) Without using your calculator, prove that .

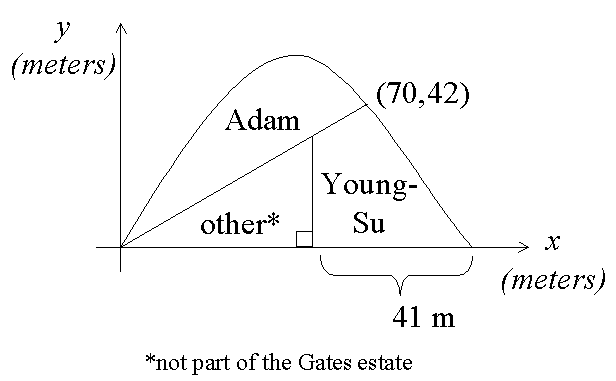
10. In his last will and testament, William H. Gates, Jr., left a small plot of land to be divided between his two sons, Adam and Young-Su. With the origin placed at the lower left corner of Adam’s plot, as shown, the curve is the parabola y = 2x – 0.02x² (don’t laugh—the state of Delaware actually has a circular arc as part of its boundary). All the other lines are straight. Which son received the larger plot of land, and by how much? (Compute at least one of the areas using exact algebra. You may use your calculator to check it and to compute the other.)

11. Compute in each case.

(a)

(b)

(c) x = 6 sin t + sin 6t
y = 6 cos t + cos 6t

(d) y = x + sin xy

12. Compute the indefinite integral in each case.

(a)

(b)

13. A force (depending on horizontal displacement x) of pounds is applied as horizontal displacement varies from 1 to 7.3 feet. Assume that work for 0<x<1 follows a different rule but achieves a total value of 388.214 foot-pounds at x = 1.

(a) To the nearest thousandth, how much additional work is done between x = 1 and x = 7.3? Be sure to show your setup and include units.

(b) Write a function (any form OK) having domain [1, 7.3] that gives total work W as a function of x.
[Note: Remember that W(1) = 388.214, and W(7.3) = 388.214 + (your answer to part a).]

W(x) = __________________________________________

(c) Compute .

(d) Explain in your own words why . In other words, why is your answer to part (c) reasonable? There is no "right" or "wrong" answer to this question—I’m just hoping for some insight into how you think about this issue. Use reverse side if necessary.

(e) Give the formal "epsilon-delta" definition of the limit of a function f (x) as x approaches c.