Algebra II / Mr. Hansen

Solution Key to March 2000 Sample Test (Ch. 9)

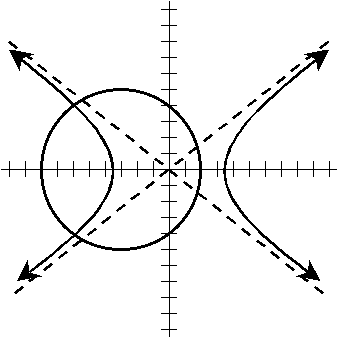
1.(a)

B² – 4AC = 2² – 4(0)(0) = 4 > 0 Þ hyperbola

(b)

B² – 4AC = 0² – 4(177)(3497) < 0 Þ ellipse
[Clearly, the answer is negative. As long as you show work in this manner, there is no need to compute the actual numeric value of the discriminant.]

(c)

B² – 4AC = 0² – 4(34)(–34) > 0 Þ hyperbola

(d)

B² – 4AC = 0² – 4(34)(34) < 0 Þ ellipse
[Actually, a better answer would be circle since the coefficients on the x² and y² terms are equal.]

(e)

Since A and B are both 0, B² – 4AC = 0 Þ parabola.

(f)

Same as part (e): parabola again.

(g)

This time B and C are both 0. Thus B² – 4AC = 0 Þ parabola.

(h)

Rewrite as –3x² + 2y² = 0 to see that A = –3, B = 0, C = 2. Therefore, B² – 4AC = 0² – 4(–3)(2) = 24 > 0 Þ hyperbola.
[Another approach is to solve the original equation for y. Taking square roots of both sides gives , which is a pair of lines passing through the origin with slopes . This pair of lines is what we would more properly call a degenerate hyperbola. The hyperbola has fused into its asymptotes and has simply become a graph in the shape of an "X."]

2.(c)

34x² – 34y² = 915
34x²/915 – 34y²/915 = 1
x²/(915/34) – y²/(915/34) = 1

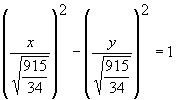
a = r_x =
b = r_y =
c² = a² + b² = 915/34 + 915/34 = 915/17
c =
Since b/a = 1, asymptotes have slope ± 1.
Center is at (0, 0).
Foci are at (–7.336, 0) and (7.336, 0).
For y-intercepts, set x = 0 in big equation above to get 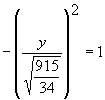. Since this is impossible [the negative of a squared expression cannot equal 1], there are no y-intercepts.

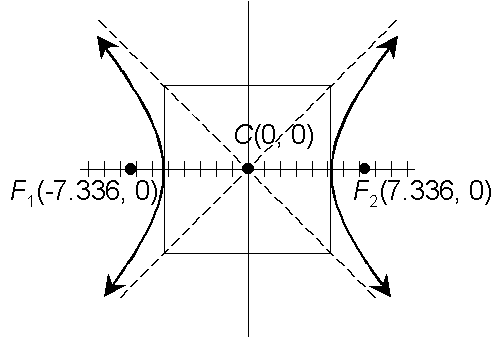
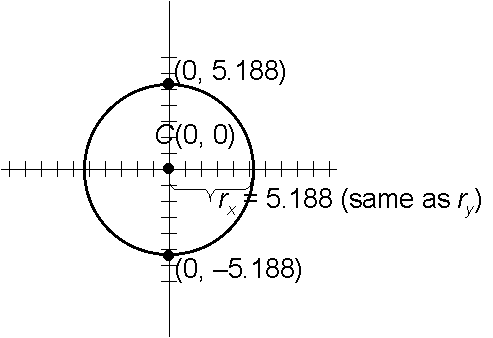
(d)

34x² + 34y² = 915
x²/34 –y²/34 = 915/34
Circle with center (0, 0) and radius

(f)

2x = 3y² – 6y + 7
2x – 7 = 3y² – 6y
2x – 7 = 3(y² – 2y)
2x – 7 + 3 = 3(y² – 2y + 1)
2x – 4 = 3(y – 1)²
x – 2 = 3/2 (y – 1)²
Vertex is at (2, 1).
To find x-intercept, set y = 0 to get x – 2 = 3/2 (0 – 1)² Þ x – 2 = 3/2 Þ x = 7/2.

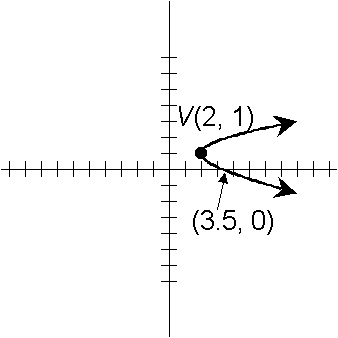
3.(a)

parabola
[It is true that we did not discuss this. However, you should be able to get this by process of elimination, since all the other conic sections are described elsewhere.]

(b)

(c)

(d)

4.(a)

Major axis: 2a = 7 – (–3) = 10 Þ a = 5
c = 4.25 (given)
c² = a² – b²
4.25² = 5² – b²
b² = 5² – 4.25² = 6.9375 = 111/16

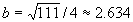
Center is halfway between the 2 given pts., namely at (–2, 2).
Equation: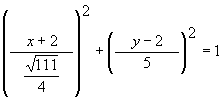
However, this problem required Ax² + Bxy + Cy² + Dx + Ey + F = 0 form. Multiplying out gives

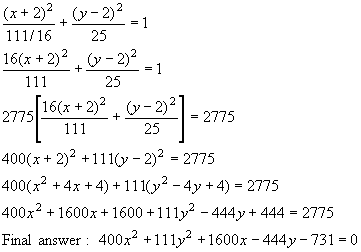
(b)

Center is where asymptotes cross, i.e., (8, 0).
Since center is on x-axis, the vertices are, too.
Vertices are 2.5 units to left and right of center.
\ r_x = a = 2.5
Since asymptote slopes are ± 3, we know ± 3 = ± b/a.
3 = b/a Þ 3 = b/2.5 Þ b = 7.5
Equation: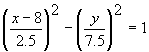

(c)

x – h = a(y – k)²
By symmetry, y-coordinate of vertex is halfway between –4 and 8, so k = 2.
Our equation is thus x – h = a(y – 2)²
We know 3 points: (5, 0), (0, –4), and (0, 8).
Plug (5, 0) into our equation from above:
x – h = a(y – 2)²
5 – h = a(0 – 2)²
5 – h = 4a
–h = 4a – 5
Now, plug either of the other 2 points [i.e., (0, –4) or (0,8)] into our equation from above:
x – h = a(y – 2)²
0 – h = a(36)
–h = 36a
Compare the 2 underlined results. Since –h = 4a – 5 and –h = 36a, we must have 4a – 5 = 36a Þ –32a = 5 Þ a = –5/32. [This value for a makes sense, because the parabola is fairly fat and opens leftward. The only remaining unknown is h.]
From above, –h = 36a Þ h = –36a Þ h = –36(–5/32) = 45/8.
Final answer: x – 45/8 = –5/32 (y – 2)²
[This equation makes sense, since it defines a leftward-opening parabola with vertex at (45/8, 2).]

(d)

r = 8/3
r² = 64/9
Equation: (x – 2/3)² + (y + 1)² = 64/9

5.

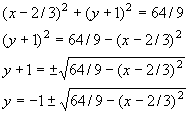
Calculator: Y₁=–1+Ö (64/9–(X–2/3)²)
[Note: Remember to use the negation sign, marked (–) on your calculator, in front of the 1. If you use the subtraction sign there, the function will not work.]
Y₂=2nd RCL VARS Y-VARS Function 1 ENTER
[For Y₂, change the + sign just before the radical to a subtraction sign.]
Display graph with ZOOM 6.
[Optional: Follow with ZOOM 5 to show circle in proper proportions.]

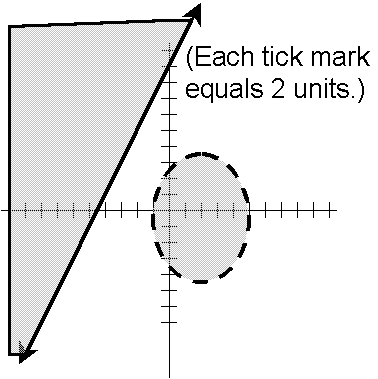
6.

16x² + 9y² – 128x + 18y < 311
16(x² – 8x) + 9(y² + 2y) < 311
16(x² – 8x + 16) + 9(y² + 2y + 1) < 311 + 16(16) + 9(1)
16(x – 4)² + 9(y + 1)² < 576
16(x – 4)²/576 + 9(y + 1)²/576 < 1
(x – 4)²/36 + (y + 1)²/64 < 1
This is the interior of an ellipse with center (4, –1), x-radius 6, and y-radius 8.
The second inequality becomes y ³ 2x + 18, i.e., the region at and above the line with slope 2 and y-intercept 18. Clearly, the regions do not overlap. Solution set: Æ .

7.

x² + y² + 6x = 16
2x² – 3y² = 24
__________________
[Various methods are possible. One is to multiply first eqn. by 3, then add.]

3x² + 3y² + 18x = 48
2x² – 3y² = 24
__________________
5x² + 18x = 72
5x² + 18x – 72 = 0

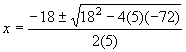
x = 2.4 or x = –6
Consider both of these cases:

First, if x = 2.4, plug into either original eqn. [second one is easier] to get
2(2.4)² – 3y² = 24
–3y² = 24 – 2(2.4)²
–3y² = 12.48
y² = –4.16
This is impossible in Â. [That is, x = 2.4 is a dead end.]

Second case: plug x = –6 into either original eqn. [second one is easier] to get
2(–6)² – 3y² = 24
–3y² = 24 – 2(36)
–3y² = –48
y² = 16
y = ± 4
Solution set: {(–6, 4), (–6, –4)}
[This makes sense if you graph the circle and hyperbola represented by the original system of equations. See optional graph below.]