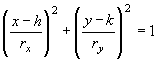
Note: Semimajor axis a is the larger of rx and ry; semiminor axis b is the smaller value. Focal radius c is found from
|
Algebra II / Mr. Hansen |
Name: _____________________________ |
|
March 2000 Practice Test on Chapter 9 |
|
Show all work
What to study
The following descriptions should be studied thoroughly (memorized, if you possibly can) and will not appear on your test sheet:
1. For any quadratic relation Ax2 + Bxy + Cy2 + Dx + Ey + F = 0, the discriminant is B2 4AC. If the discriminant is negative, the relation is an ellipse (or circle if A = C). If the discriminant is positive, the relation is a hyperbola. Finally, if the discriminant is zero, the relation is a parabola. Memory aid: "NEC, PH, ZP." NEC is a Japanese company that makes cell phones, theater TVs, computers, etc. PH (pH) is a measure of acidity, in case youve had any chemistry. Finally, ZP (zap) is what you get by process of elimination.
2. Equation of circle with center (h, k) and radius r:
(x h)2 + (y k)2 = r2
3. Equation of ellipse with center (h, k), x-radius rx, and y-radius ry:
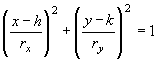
Note: Semimajor axis a is the larger of rx and ry; semiminor axis b is the smaller value. Focal radius c is found from
4. Equation of hyperbola with center (h, k), x-radius rx, and y-radius ry:
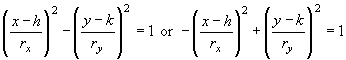
Note: The first form gives branches that open left and right. (Memory aid: x positively reminds you of left and right.) The second form gives branches that open up and down. (Memory aid: y positively reminds you of up and down.) With hyperbolas, a is always rx, and b is always ry. Focal radius c is easier than for ellipses:
5. Equation of parabola with vertex (h, k):
The first form
[ x h = a(y k)2 ] opens right if a > 0, left if a < 0. (Memory aid: since (y k)2 is always positive, x takes its cue from the sign of a. Rightward values of x tend to be positive, and leftward values tend to be negative.) The second form [ y k = a(x h)2 ], which we studied last fall, opens up if a > 0, down if a < 0. (Memory aid: since (x h)2 is always positive, y takes its cue from the sign of a. Upward values of y tend to be positive, and downward values tend to be negative.)Cued formulas
The following formulas will be printed on your test sheet. Of course, since they are missing the explanations shown above, they will be of no use to you unless you have studied the list above very carefully. Here is exactly what you will see on your test sheet:
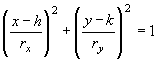 , c2 = a2 b2
, c2 = a2 b2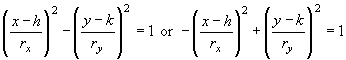 , c2 = a2 + b2, asymptote slopes ± b/a
, c2 = a2 + b2, asymptote slopes ± b/aSkill areas
2. Given a sketch of a quadratic relation, be able to produce its equation. In most cases, the "x h, y k" form will be sufficient. However, you should be able to produce the Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 form as well.
3. Given a system of quadratic and/or linear relations in x and y, be able to find the solution set algebraically as well as graphically. Remember that your answer must be expressed as Æ if there are no points of intersection, or otherwise as a set of ordered pairs.
Additional problems
If you need more practice problems on any of the skill areas listed above, please locate suitable problems in the textbook. For example, the review problems at the end of Chapter 9 are an excellent source of practice problems. If you need additional guidance, please leave a voice mail message at (703) 599-6624 (available 24 hours).
|
1. |
Use the discriminant to identify each of the following conic sections. |
|
|
(a) |
|
|
|
(b) |
|
|
|
(c) |
|
|
|
(d) |
|
|
|
(e) |
|
|
|
(f) |
|
|
|
(g) |
|
|
|
(h) |
|
|
|
2. |
|
|
|
3. |
|
|
|
(a) |
|
|
|
(b) |
|
|
|
(c) |
|
|
|
(d) |
|
|
|
4. |
|
|
|
(a) |
|
|
|
(b) |
|
|
|
(c) |
|
|
|
(d) |
|
|
|
|
|
|
|
|
|
|
|