1.(a)
Note: Omitting the absolute value bars on x would be considered a minor error. We need the absolute value bars, because when we take the 4th root of x4, we must always get a nonnegative value (even though x itself could be negative). This is similar to the reason for saying 
.
1.(b)
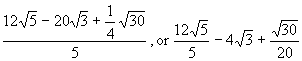
(Either form is acceptable.)
1.(c)
(Again, either form is acceptable.)
1.(d)
1.(e)
2.
-1.645 ´ 10-890
3.(a)
S = {-1.479}
Note: This is an approximate answer that you get by using your calculator to find the root of the polynomial equation y3 + 9y2 + 26y + 22 = 0. If you simply used your root finder to solve the original equation, you would get the right answer but would lose a few points for failing to demonstrate your knowledge of the general procedure (see flowchart on p.427).
Additional notes: You should check your answer by "STOing" it into Y and seeing whether Y minus the cube root of Y+5 gives you -3. (If that last sentence made no sense to you, please look at the original equation; Y minus the cube root of Y+5 should equal -3 if the original equation is being satisfied.) However, since there are no irreversible steps involved, you would not lose any points by failing to check your answer. Because cubing both sides of an equation is reversible, there is no danger of extraneous roots in problem 3.(a).
3.(b)
S = {1393/144}
Note: There was an irreversible step involved. For full credit, you must check this answer and indicate (perhaps with a check mark) that it works in the original equation.
3.(c)
S =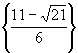 
Note: There was an irreversible step involved. For full credit, you must indicate (perhaps with a check mark) that this root works in the original equation and (perhaps with an "X") that you are rejecting the other one. You need not state the answer in simple radical form. For example, you could write the solution set as {(33 - Ö 189)/18} or as {1.070}. Don't write {1.069}, however, since that would be a rounding error.
3.(d)
S =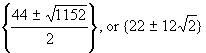 
, or {38.971, 5.029}
(Any of these forms would be acceptable.)
Note: There was an irreversible step involved. For full credit, you must indicate (perhaps with check marks) that both roots satisfy the original equation. On your calculator, you can do the quadratic formula work and check your answers quite efficiently, as follows:
Step 1: (44+Ö (442-4*1*196))/2 ENTER
Purpose of Step 1: We have just applied the ______________________ to find one of the two __________ of the equation p2 - 44p + 196 = 0.
Step 2: Press STO key followed by ALPHA A ENTER to store result into A.
Step 3: Press 2nd ENTRY 2nd ENTRY to recall the expression from Step 1.
Step 4: Press 2nd ¬ (left arrow) to get to beginning of line. (You don't have to, but this is a nice shortcut.) Then change the + sign to a - sign, press 2nd ® (right arrow) to get to end of expression, then press STO key followed by ALPHA B ENTER to store result into B.
Purpose of Steps 2 and 4: We now have the two possible solutions stored in our calculator under the names ____ and ____ .
Step 5: Please look at the original equation. Are you looking at it? Good. Now key in Ö (2A)-Ö (A-5) ENTER. If A is a solution, what number should the calculator display when you press ENTER? _____________ Is that what you got? _____
Step 6: Press 2nd ENTRY to recall the expression from Step 5. Change each A to a B and press ENTER. If B is a solution, what number should the calculator display when you press ENTER? _____________ Is that what you got? _____
4.
Since 88 ft/sec = 60 mph (true fact that you were asked to learn), 44 ft/sec must be 30 mph. Thus if we let x = headwind speed (mph) and y = maximum riding speed (mph), we have the general equation y = k/x2. Since y = 30 when x = 5, k = 750. Therefore, the particular equation is y = 750/x2. When x = 10, y must be 750/102, which you should be able to compute in your head. Answer: 7.5 mph.
5.(a)
Let d = snow depth (inches), x = # of sophs., y = shoveling time (minutes).
General eqn.: y = kd2/x0.88
5.(b)
When 2 students are shoveling 10 inches of snow (i.e., d = 10 and n = 2), we have y = 45. That is the same as saying 45 = k(102)/20.88. We can solve for k to get k = 0.45 (20.88). You should either leave k in this exact form or "STO" it into K on your calculator to avoid losing accuracy.
Particular eqn.: y = 0.45d2 (2/x)0.88
5.(c)
Algebra method: We want y < 20, i.e., y = 0.45d2 (2/x)0.88 = 0.45(64) (20.88/x0.88) » 53.0028/x0.88 < 20. Solving this inequality gives 1/x0.88 < 20/53.0028 Þ x0.88 > 53.0028/20 » 2.65014. Taking 0.88 roots of both sides or (groan) using logarithms gives x > 3.0268. Answer: We need at least 4 sophomores.
Calculator method: Store 8 into D (keystrokes are 8 STO ALPHA D ENTER). Hit your "Y=" key and put the particular equation from part (b) into Y1. Then make a table of values: 2nd TBLSET (set TblStart=1, D Tbl=1, Auto, Auto) followed by 2nd TABLE. You'll notice that the shoveling time (Y1) decreases as X increases. Time drops below 20 when X reaches 4. Answer: We need at least 4 sophomores.
Note: To describe your calculator method, you need to write a sentence. The following would suffice. "I put the particular equation into Y1, set D to 8, and made a table that showed time < 20 whenever # of sophs. > 3." Technically, you should write another sentence to show you know why Y1 is always decreasing as X increases (reason: for fixed D, the equation is of the form y = Cx-0.88 where C is a positive constant; thus y is a decreasing power function). However, the quoted sentence is fine for now. In precalculus you will need to be more thorough.
There are other ways to use your calculator, too. One would be to put the particular equation from part (b) into Y1, put the constant value 20 into Y2, and see where the graph of Y1 falls below the graph of Y2. The intersection of Y1 and Y2 (keystrokes: 2nd CALC intersect ENTER ENTER ENTER) will occur just a little to the right of X=3, which tells us that 4 students are necessary.
5.(d)
With 24 stored into D, we get a curve for Y1 that seems ridiculous for X=1 (477.03 minutes, or almost 8 hours). That is probably too high. With 5 sophomores working (X=5), the model claims that nearly 2 hours would be needed, which is almost 10 person-hours. Although the loss of efficiency (represented by the exponent 0.88, which is less than 1) is reasonable for short jobs, for a job this long and arduous, we should expect an improvement in efficiency as more workers are added. After all, 5 people working outdoors for a couple of hours would have much higher morale than 1 person working alone for an entire day. Thus we can say that the model needs to be revised for large values of d.
The model also malfunctions for large values of n. Do you really believe that 72 sophomores could clear 2 feet of snow in slightly over 11 minutes? In the real world, it might take 10 or 15 minutes just to get the people's attention and issue them their snow shovels.
Incidentally (this was not part of the question), there is also a problem with small values of d. For example, the model predicts that an inch of snow (d = 1) could be cleared in 0.2 minutes (about 12 seconds!) by a team of 5 sophomores.
There is no single right or wrong answer to this question. The purpose was to get you to think a bit.
5.(e)
Provided d > 0, the answer is no, because if we temporarily hold d constant, the equation in part (b) defines a power function with positive constant of proportionality and domain N (i.e., natural numbers), and such power functions return only positive values.
However, if d = 0, then y = 0 everywhere (regardless of the number of students). This result agrees with the real world, since 0 snowfall requires 0 shoveling time.
6.(a)
In f, y = (15x - 5)3/5.
In f -1, x = (15y - 5)3/5.
Solve for y [steps omitted]: y = x5/3/15 + 1/3
Answer: f -1(x) = x5/3/15 + 1/3.
6.(b)
The term "identity function" means the function y = x, since this is the function that does not change its input in any way. (Give me an x, and I'll give you a y that is exactly the same as the x you gave me.) Basically, you need to show that for any legal x value, f -1( f (x) ) = x, and f ( f -1(x) ) = x. "Legal" in this question is not anything to worry about, since the domain for both f and f -1 is  . The algebra is a bit tedious, but if you substitute carefully and start with either f -1( f (x) ) or f ( f -1(x) ), you will get x. Each one requires 4 or 5 steps. You can't "eyeball" these to get the result.
Just as you might put two D cells into a flashlight to make a single "battery power unit," you can think of joining the kachunka machine for f and the kachunka machine for f -1 into a single giant kachunka machine. When we put x into this giant kachunka machine, what comes out the other end?
What we are really saying is that the "composite function machine" consisting of f followed by f -1 does not change x. Similarly, f -1 followed by f does not change x. Since it is difficult to explain this process on paper, we'll go through the steps in class. Be sure to ask if you had trouble proving f -1( f (x) ) = x, or f ( f -1(x) ) = x.
6.(c)
You should be able to do this if you solved part (a). Press the "Y=" key, and define Y1 and Y2 as shown by the definitions of f and f -1. Suggestion: Start with ZOOM 6 (ZStandard), then use ZOOM 5 (ZSquare) to reduce the screen distortion. Do you notice how the graphs are mirror images across the line y = x? ________ At what point do the graphs intersect? ( _____ , _____ ) If g is any invertible function whatsoever, can you say that g and g-1 must cross somewhere? _____ What can you say about the x and y coordinates at any point where g and g-1 cross? _________