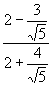Algebra II / Graham, Hansen, James

Name: _____________________________

Feb. 2000 Practice Test on Chapter 8

 

The purpose of this practice test is to help you review by showing you the wording and types of problems on the actual test. The actual test is a bit shorter and contains different problems. Although most of these practice problems are similar to real ones, not all types of problems are represented here. See the review problems in §8-7 for additional examples. Mr. Hansen’s students are also required to know inverse functions, which may be retested because of the disappointing results on the Chapter 6 test.

No notes
You cannot use notes on the actual test. Ample room to write will be provided. In the unlikely event that you need extra space, scratch paper will be provided. Note, however, that this practice test has been written with the problems scrunched together. For the practice test, write small or write solutions on a separate sheet.

Calculator
You may use your calculator on all parts of the test. However, since your work is what will be graded, not your answer, in most cases you should use your calculator only to check your work. Decimal answers are acceptable only when the problem says "round to ____ places" or "round to the nearest _____ ."

Simplifying
The word "simplify" means to leave everything in simplest form (e.g., write 2Ö 2 instead of Ö 8 in your final answer), with no radicals in the denominator, and in a + bi format in the case of complex numbers.

Show all work
For full credit, show all work. Correct answers that could be obtained through mere button-pushing on the calculator will usually receive NO CREDIT. Reduce fractions to simplest form and rationalize all denominators. Give exact answers (no decimals) unless otherwise requested.

Units of measure
Show units of measure where appropriate.

Simple radical form
You need to know (in a practical sense) the definition of simple radical form on p.419 of your textbook. You will not be required to write the definition, but you will be required to simplify expressions and give answers in simple radical form. The definition will not appear on the test.

1.

Simplify without using a calculator. Express answers in simple radical form (as defined in your book). Use no decimal approximations, no negative exponents, and no radicals in the denominator. You may use your calculator to check your work and are encouraged to do so if time permits.

 

(a)

 

(b)

 

(c)

 

(d)

 

(e)

 

2.
Compute and express in scientific notation with at least 4 significant figures in the mantissa:

 

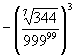
3.
Solve for the unknown, and express answer in appropriate set notation. Try to give exact answer (no decimals). If there is no way to calculate exact form, give an approximation correct to at least 3 places after the decimal point. One of these 4 problems requires a calculator at one point. Show all work to justify your solution.

 

(a)

 

(b)

 

(c)

 

(d)

 

4.
On a track bike (a racing bicycle with a single fixed gear ratio of approximately 4:1), your maximum velocity over a suitable domain varies inversely with the square of the velocity of any headwind you encounter. If you can ride 44 ft/sec (briefly) into a 5 mph headwind, how fast can you ride into a 10 mph headwind? Show your work, and express your answer in mph.

 

5.
The length of time it takes a group of sophomores to remove snow from a certain sidewalk varies directly with the square of the snowfall depth and inversely with the 0.88 power of the number of sophomores present. From past experience, I know that 2 sophomores could shovel 10 inches of snow from this walk in 45 minutes.

 

(a)
Define your variables and write the general equation.

 

(b)
Write the particular equation.

 

(c)
If the first snowfall of 2001 is 8 inches, how many sophomores would be needed to shovel the entire walk in less than 20 minutes? Either answer the question using algebra, or describe (approx. 1 sentence) your calculator technique.

 

(d)
In January 1987, a pair of blizzards—one on Friday, one on Sunday—buried the Washington area under approximately 2 feet of snow. Some schools were closed for 2 weeks, and most were closed for at least a week. Does your mathematical model give reasonable results for a 2-foot shoveling job? Explain.

 

(e)
According to this model, is there any number of sophomores that could reduce the shoveling time to zero? Explain.

 

6.
Let f(x) = (15x – 5)3/5.

 

(a)
Find the inverse function.

 

(b)
Prove algebraically that f –1 is both a left and a right inverse. In other words, prove that f composed with f –1, in either order, yields the identity function.

 

(c)
Plot f and f –1 on the same set of axes.