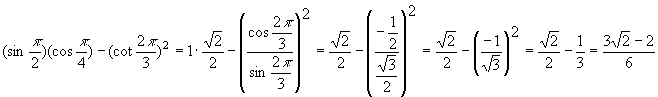
If the work is as shown above, or essentially as shown above, then either
|
Algebra II / Mr. Hansen |
Answer Key to 5/5/2000 Sample Test (Ch. 13) |
If you have any questions, leave a voice mail message at (703) 599-6624. This number is available 24 hours a day, so don't worry about calling at an odd hour. Be sure to state your number and a suitable time to call you back. Please DO NOT send e-mail, since the system is still unreliable following the ILOVEYOU virus.
This answer key shows the work that you would be required to show for full credit.
1,2. [See notes from Fridays class or consult your textbook. On the actual test, you may be asked to work with different trig functions or different quadrants. For example, you may have to write the sine, secant, and cotangent of all angles in the first and second quadrants.]
3. For example, csc 180° = 1/(sin 180° ) = 1/(1/2) = 2. You would label the terminal point of the 180° ray with the marking "csc 180° = 2" for full credit. Merely writing the number 2 floating somewhere, or the incorrect notation csc = 2, would not earn credit. Also note that writing "csc 180 = 2" would earn no credit, since any angle shown without a ° symbol is assumed to be in radians.
4. For example cot 225° = cos 225° / sin 225° = 1 since the sine and cosine are equal for an angle of 225°. You would label the terminal point of the 225° ray with the marking "cot 225° = 1" for full credit. Merely writing the number 1 floating somewhere, or the incorrect notation cot = 1, would not earn credit. Also note that writing "cot 225 = 1" would earn no credit, since any angle shown without a ° symbol is assumed to be in radians.
5.(a) 0.965 (no work required)
Calculator keystrokes: MODE Degree 2nd QUIT cos(15 2nd ANGLE ° 14 2nd ANGLE ') ENTER
or . . . MODE Radian 2nd QUIT cos((15+14/60)2nd ANGLE ° ) ENTER
5.(b) 1.573 (no work required)
Calculator keystrokes: MODE Degree 2nd QUIT 1/tan(12 2nd ANGLE r) ENTER
or . . . MODE Radian 2nd QUIT 1/tan(12) ENTER
5.(c) 0.150° or 9'0.0" or 0.00262 radians (no work required)
Recommended thought process:
We want "the angle whose cosecant is 382"
= "the angle whose sin is 1/382"
= "the arcsin of 1/382"
= sin1(1/382)
Calculator keystrokes: MODE Degree 2nd sin1(1/382) ENTER 2nd ANGLE 4 DMS ENTER
or . . . MODE Radian 2nd sin1(1/382) ENTER
6. Only part (c) is an angle. Since the answers to parts (a) and (b) are merely numbers, only part (c) gives you a choice of displaying your answer in radians or degrees. Three answers are shown above. You should be equally comfortable giving your answer in radians, decimal degrees, or degrees/minutes/seconds.
7.(a) 
If the work is as shown above, or essentially as shown above, then either ![]()
![]() or
or ![]() would qualify for full credit as the final answer. If work is spotty or incomplete, no answer (even a correct one) would qualify for full credit. The answer 0.374, which happens to be correct to 3 decimal places, would receive no credit. Although you are expected to use your calculator to check your answer, your work is to be performed using exact arithmetic (no decimals) throughout.
would qualify for full credit as the final answer. If work is spotty or incomplete, no answer (even a correct one) would qualify for full credit. The answer 0.374, which happens to be correct to 3 decimal places, would receive no credit. Although you are expected to use your calculator to check your answer, your work is to be performed using exact arithmetic (no decimals) throughout.
7.(b) For the first term you may make use of the fact that sin(sin1 x) = x regardless of the value of x. This is true from common sense alone, in the same way as "the nickname of the person whose nickname is Slammer" equals Slammer. What we are saying is "the sine of the angle whose sine is x" equals x. Think it through logically in your mind. What else could sin(sin1 x) be? Answer: nothing.
The second term is trickier, though. "The person whose nickname is (the nickname of Mr. Hillsamer)" would be "the person whose nickname is Slammer"which might not be uniquely identified as Mr. Hillsamer. (There might be a rap star known as Slammer who is more famous than our Mr. Hillsamer.) In the same way, tan1(tan 3p) might not equal 3p, even though the arctangent and tangent functions are inverses. Remember, to avoid ambiguity we defined the arctangent function to have its range in quadrants I and IV conjoined, i.e., running from 90° to 90° (p/2 to p/2 radians). For example, we say tan1(1) = 45°, not 315°, even though technically both answers are somewhat correct. To be totally correct we must make sure our arctangent function has a result that falls between p/2 and p/2 radians.
Therefore, tan1(tan 3p ) = tan1(0) = 0° or 0 radians, not 3p radians.
Here is the work you would be expected to show: sin(sin1 1/14) + tan1(tan 3p ) = 1/14 + tan1(0) = 1/14 + 0 = 1/14. Any lesser amount of work than this would not earn full credit, since you have not shown at each step that you know what youre doing. With your calculator in radian mode, you can quickly verify that your answer is correct. The answer 1/14 or 0.071 by itself would earn no credit.
8.(a) Yes, f is periodic because it repeats itself every year.
(b) The period is one year (approx. 365.25 days).
(c) Yes, f is approximately sinusoidal.
(d) By f (0) we mean the length of daylight observed at National Cathedral on Dec. 21, or about 9.43 hours, since according to the U.S. Naval Observatory (at http://mach.usno.navy.mil/cgi-bin/aa_pap), the actual value for 12/21/1999 is 9 hr., 26 min. An answer of 9 hr. is a perfectly acceptable estimate.
(e) Please note: For B, you must use the formula (and show the work) B = 2p /period. The other values can be "guesstimated" based on your common sense.
A = amplitude = (peak-to-peak change)/2 = (14 hr., 54 min. 9 hr., 26 min.)/2 = 2 hr., 44 min. » 2.633 hr.
Acceptable estimate: A » 3 hr.
B = 2p/period » 2p/365.25 days » 0.017202424 days
Acceptable estimate: B » 2p/365 » 0.0172 days. You must show work for this one.
C = vertical shift of centerline = midpoint between longest and shortest day = 12 hr., 10 min. » 12.167 hr.
Acceptable estimate: C = average length of daylight » 12 hr.
D = phase shift = # of days before daylight is at its maximum = 1/2 year » 365.25 days / 2 = 182.625 days
Acceptable estimates: D = 1/2 year » 182.5 days (or 182, or 183).
(f) Using the (corrected) formula from the Formula Bin, we have y = C + A cos B(x D). Plugging in values for A, B, C, and D gives one of the following:
Using accurate values, y = 12.167 + 2.633 cos 0.017202424(x 182.625).
Using rough estimates, y = 12 + 3 cos 0.0172(x 182.5).
Both curves (accurate and rough) are plotted below. As you can see, there is not a huge difference between them.
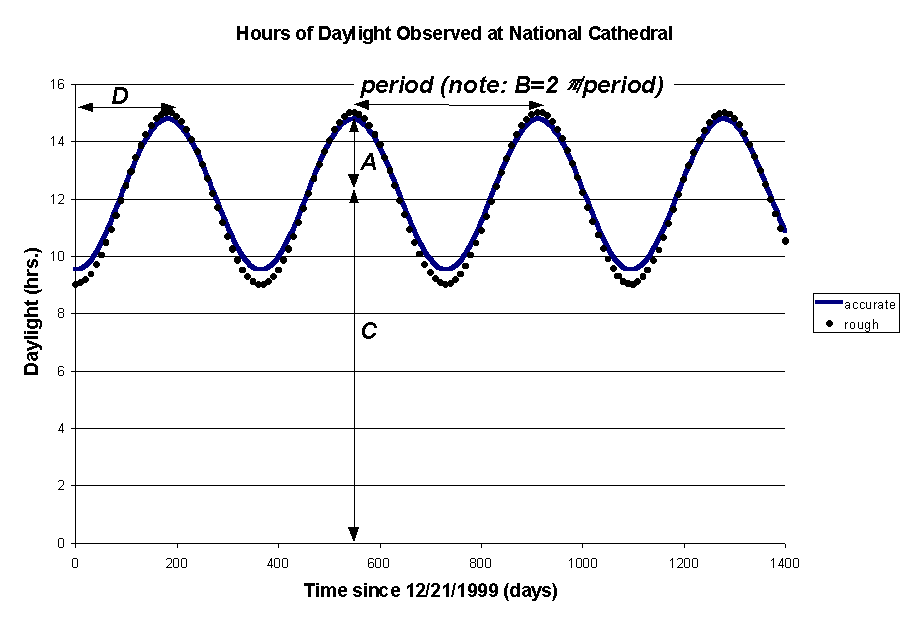
How to do this on your calculator: First, choose a set of values for A, B, C, and D. Then STO them using 2.633® A, 2p /365.25® B, etc. (or 3® A, 2p ® B, etc.), and hit your Y= key to define Y1=C+Acos(B(XD)). Set your WINDOW to be [0, 1400] ΄ [0, 16] and press the GRAPH key.
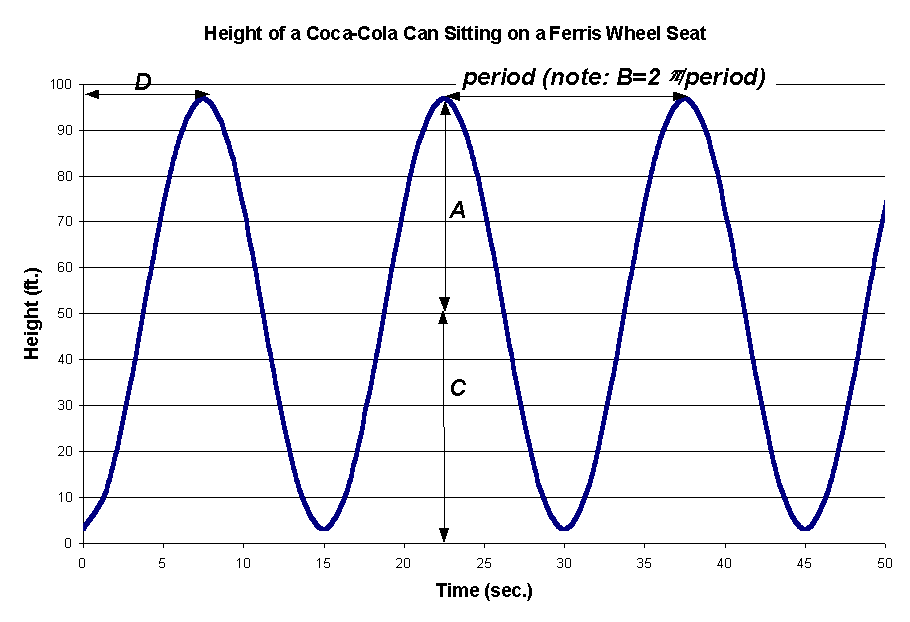
9.(a) Yes, f is periodic because it repeats itself every 15 seconds.
(b) The period is 15 sec.
(c) Yes, f is approximately sinusoidal.
(d) By f (0) we mean the height of the Coca-Cola can at time t = 0 sec. Because the problem does not state where the can starts, we may assume that the can starts in the lowest seat position (y = 3 ft.).
(e) Please note: For B, you must use the formula (and show the work) B = 2p/period. The other values can be determined quickly by drawing a picture either on paper or in your mind.
A = amplitude = (peak-to-peak change)/2 = (97 3)/2 = 47 ft.
B = 2p/period = 2p/15 » 0.41888 sec.
C = vertical shift of centerline = height of axle = 50 ft.
D = phase shift = # of seconds before Coca-Cola can reaches its maximum height = 7.5 sec.
(f) Using the (corrected) formula from the Formula Bin, we have y = C + A cos B(x D). Plugging in values for A, B, C, and D gives y = 50 + 47 cos 0.41888(x 7.5). The graph is plotted below with a window of [0, 50] ΄ [0, 100].