Algebra II / Mr. Hansen

Name: _____________________________

4/20/2000 Partial Practice Test on §§12-1 through 12-6, plus Binomial Theorem

 

Show all work
For full credit, show all work. You may use your calculator in any way that you wish, including study aids stored into your calculator's memory, but you must show sufficient work on your paper to demonstrate clearly that you understand the concepts. For example, if you assert that the number of ways of doing something is 6, you should provide a justification such as 4C2 = 6. An exception would be if the answer is obvious (e.g., the total number of equally likely outcomes of a fair die is clearly 6).

"Immunization"
For Mr. Hansen's class only, you have an optional assignment with a due date of Friday, April 21. In addition to the problems on this practice test, which cover only a portion of the material that will be tested, you may wish to work some homework problems. For each correct homework problem that you turn in on Friday, April 21 (written on a sheet labeled "SAMPLE TEST PROBLEMS"), you can "immunize" yourself against a test problem of the same type. For example, if you do a problem such as #16 on p.670 and get it correct, but you miss a very similar problem when it appears on the test, you will lose only half as many points as you otherwise would have lost. Immunization will also apply to the problems on this sample test if you turn them in with adequate correct supporting work.

Notation
You are expected to be familiar with the following notation. Fill in the blanks as appropriate (see, for example, the notes on p.663).
nPr
nCr

P(A)
P(A Ç B) = P(A _____ B) = P(A) · P(B) provided _________________________________________________
P(A È B) = P(A _____ B) = P(A) + P(B) provided __________________ ; otherwise P(A È B) = P(A) + P(B) – _________
P(~ A) = _______________
P(A but not B) = ________________________________________

1.

Compute (–4x3 – 2y4)7. Simplification of the binomial coefficients is optional.

 
2.
Compute the term containing p93 in the expansion of (2a – 3p3)33. Simplify fully this time.

 
3.
Prove that for any positive integer n, 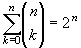. If you can't prove this in general, show that the equation is true when n = 3 and also when n = 7.

 
4.
Compute the probability of drawing one pair (i.e., 2 cards of the same value) when

 

(a)

2 cards are drawn with replacement from a standard 52-card deck that is shuffled in between the draws

 

(b)

2 cards are drawn without replacement from a standard 52-card deck

 

(c)

5 cards are drawn without replacement from a standard 52-card deck

 
5.
Compute each of the following. Show both the notation (e.g., nPr or nCr) and the numeric answer.

 

(a)

In how many ways can a committee of 4 sophomores be selected from a class of 72 sophomores?

 

(b)

In how many ways can a 6-character license plate be formed from the letters of the alphabet, the digits, and the special characters blank, hyphen, and © ? Assume that repeats are not allowed.

 

(c)

Answer part (b) assuming that repeated characters are allowed.

 
6.
Let A be the event that it is raining outside, and let B be the event that a randomly selected person is using an umbrella (assuming that it is raining). Assume that P(A) = 0.15 and P(B) = 0.4. (Technically, we should say P(B | A) = 0.4. In other words, 0.4 is the probability of B given that A is true. A and B are not independent, since clearly the presence or absence of rain has an effect on people's probability of using an umbrella.)

 

(a)

Compute P(A Ç B) and explain what this means in English.

 

(b)

Compute P(~ A) and explain what this means in English.

 

(c)

Compute P(~ B) and explain what this means in English.

 

(d)

Compute P(A Ç ~ B) and explain what this means in English.

 
7.
Approximately 3% of the people in a certain large town have the surname Smith. If you randomly select 2 people, what is the probability that

 

(a)

both are named Smith?

 

(b)

neither is named Smith?

 

(c)

at least one is named Smith?

 
8.
In problem 7, compute the probability that

 

(a)

of 100 randomly selected people, none are named Smith

 

(b)

of 100 randomly selected people, at least one is named Smith

 
9.
Give an example of a random event that has probability exactly equal to 2/3, and verify your calculation using the formula(s) that you have learned.