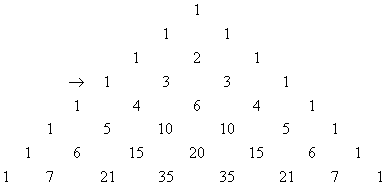
|
Algebra II / Mr. Hansen |
Answer Key to April 2000 Sample Test (Ch. 12) |
If you have any questions, leave a voice mail message at (703) 599-6624. This number is available 24 hours a day, so don't worry about calling at an odd hour. Be sure to state your number and a suitable time to call you back.
This answer key shows answers only. As you know, work is required for credit.
1. Answer (fully simplified):
16384x21 57344x18y4 86016x15y8 71680x12y12 35840x9y16 10752x6y20 1792x3y24 128y28
Alternate answer with everything simplified except the binomial coefficients:
16384x21 7C1(8192x18y4) 7C2(4096x15y8) 7C3(2048x12y12) 7C4(1024x9y16) 7C5(512x6y20) 7C6(256x3y24) 128y28
Please note that you would not earn full credit if you left the "powers of a power" unexpanded.
2. Approx. 1.305 ´ 1018 a2p93
3. Recall Pascals Triangle (the top row, with the single 1 in it, corresponds to n = 0):
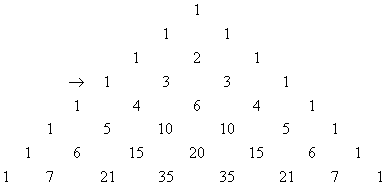
In the n = 3 row, which is marked with an arrow above, the coefficients are ![]() . You can see that they add up to 8, which is what the equation claimed (since 23 = 8). Thus the equation is true when n = 3.
. You can see that they add up to 8, which is what the equation claimed (since 23 = 8). Thus the equation is true when n = 3.
In the n = 7 row, which is the row with the 7 in it, you can see that 1 + 7 + 21 + 35 + 35 + 21 + 7 + 1 = 128, which equals 27. That proves that the equation is also true when n = 7.
To prove the equation in general, you have to apply a clever trick of writing the RHS of the equation as 2n = (1 + 1)n. Now perform a binomial expansion to get ![]() , which simplifies to
, which simplifies to ![]() , which is the LHS of the equation as desired.
, which is the LHS of the equation as desired.
4.(a) 1/13 (no work required)
(b) 1/17 (work required)
(c) 352/833 (work required)
5.(a) 72C4 = 1,028,790
(b) 39P6 = 2,349,088,560
(c) 396 = 3,518,743,761
6.(a) 0.06 (work required)
If we randomly select a person at a random time, there is a 6% chance that what we choose is a rainy day AND a person who is using an umbrella. [Note: The multiplication rule is valid here since the umbrella probability is actually P(B | A), the probability of B assuming that A is true.]
(b) 0.85 (work required)
If we randomly select a time, there is an 85% chance that rain is not falling.
(c) 0.6 (work required)
If we randomly select a person (assuming that rain is falling), there is a 60% chance that the person is umbrella-less.
(d) 0.09 (work required)
If we randomly select a person at a random time, there is a 9% chance that what we choose is a rainy day AND a person who is NOT using an umbrella. [Note: The multiplication rule is valid here since the umbrella probability is actually P(~B | A), the probability of ~B assuming that A is true.]
7.(a) 0.0009 (work required)
(b) 0.9409 (work required)
(c) 0.0591 (work required)
8.(a) Approx. 0.04755 (work required)
(b) Approx. 0.95245 (work required)
9. One rather complicated example would be the event of rolling a fair die and obtaining a value that is a divisor of 6. You can surely come up with something simpler. Justification:
P(divisor of 6) = P(1 or 2 or 3 or 6) = P(Œ È È
Ž È
‘) = P(Œ) + P() + P(Ž) + P(‘) = 1/6 + 1/6 + 1/6 + 1/6 = 4/6 = 2/3. The addition rule is valid because the four successful die outcomes are mutually exclusive.