Algebra II / Mr. Hansen

Name: _____________________________

April 2000 Practice Test on §§11-1 through 11-7

 

Show all work
For full credit, show all work. You may use your calculator in any way that you wish, including study aids stored into your calculator's memory, but you must show sufficient work on your paper to demonstrate clearly that you understand the concepts. For example, if you assert that t9 = 44, you should provide the formula and the work to justify your claim.

Formula card
You may use a formula card containing the five key formulas we studied. These will not be provided for you on the test.

 

arithmetic

geometric

 

nth term

tn = t1 + (n - 1)d

tn = t1rn - 1

 

partial sum of n terms

Sn = (t1 + tn) · n / 2
Sn = t1 · (1 - rn) / (1 - r)

 

infinite sum

NOT APPLICABLE
S¥ = t1 / (1 - r) if |r| < 1

 

1.

Define "sequence" and "series" and describe the difference between them.

 
2.
Give an example of . . .

 

(a)
an arithmetic sequence with common difference -2.5

 

(b)
a series that is neither arithmetic nor geometric

 

(c)
a geometric series with common ratio 21/3

 

(d)
an arithmetic sequence with d > 0 and tk < 0 for all k Î N

 

(e)
a geometric sequence with r < -2 and t1 = 7

 
3.
Consider the infinite series -1 + 1 - 1 + 1 - 1 + . . .

 

(a)
What is t1?

 

(b)
Is this a geometric series? ____ If yes, what is r? ____ If no, what kind of series is this? ______________

 

(c)
Compute the sum of the series.

 
4.
There will be a problem similar to S1 or S2 on p.601. In other words, find tn and Sn if you are given a few key facts.

 
5.
Find . . .

 

(a)
the geometric mean between 17 and 289 (bonus: give a second possible answer, and explain why it is seldom used)

 

(b)
three arithmetic means between 17 and 289

 

(c)
two geometric means between -12 and -11 (i.e., find two that are unequal in magnitude)

 
6.
There will be a problem similar to #27, 30, or 32 on p.588. In other words, be able to apply the formulas from your formula card in creative ways, combining ideas where necessary.

 
7.
There will be a problem similar to S4 on p.601. It may be cast as a word problem, however. Here is one way of doing that:

Bob's Bashing & Building Corp. (BB&BC) is using a pile driver to pound a wooden piling into a sandy area as part of the process of constructing a foundation for a new beach house. The first stroke of the pile driver drives the piling 100 cm into the ground. The second stroke drives the piling 80 cm, the third stroke 64 cm, and the pattern continues indefinitely.

 

(a)
How far does the fourth stroke drive the piling? The fifth stroke?

 

(b)
After 20 strokes, how far has the piling been driven into the ground?

 

(c)
What is the maximum depth that the piling will reach?

 
8.
There will be a problem similar to S6 or S7 on p.602. In other words, be able to solve general problems involving sequences or series, including inequalities such as S6.

 
9.
There will be an interest-related word problem similar to #5 on p.603.

 
10.
There will be a geometric series problem similar to #14 on p.606. Although the series given in that problem does not converge (since r = _______ ), the series on the test that you take Friday may converge.

 
11.
Write sigma notation for each of the following:

 

(a)
2 + 4 + 6 + 8 + . . .

 

(b)
1/2 + 2/3 + 3/4 + 4/5 + . . .

 

(c)
9 + 6 + 3 + 0 - 3 - 6 - 9 - 12 - 15 - 18 - 21 - 24 - . . . - 309

 
12.
State 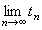for 11(a) and 11(b).

 
13.
Compute the value of each of the series in #11.