1. A sequence is an ordered set of terms separated by commas. (Technically, it is a function with domain N or W, but this technical definition is not very helpful.) A series is basically nothing more than a sequence with the commas replaced by plus signs, i.e., the sum of the associated sequence of terms.

2.(a) 6, 3.5, 1, -1.5, -4, -6.5, . . . [note: it would be an error to use plus signs]

2.(b) 7 + 8 + 7 + 8 + 7 + 8 + . . .

2.(c)

2.(d) In plain English, this says we have to find an infinite increasing arithmetic sequence with terms that are all negative. There is no way this can be done, since eventually the terms will become positive if we have a positive common difference. Answer: IMPOSSIBLE.

2.(e) 7, -21, 63, -189, . . .

3.(a) -1

3.(b) yes, geometric, with r = -1

3.(c) DNE (impossible), since |r| is not less than 1

4. Solutions to S1 and S2 are available here.

5.(a) 17 times the square root of 17, or approximately 70.093
BONUS: -70.093, which is usually ignored. The value -70.093 is legitimate since r could be either plus or minus the square root of 17. Using the positive value for r gives the standard answer for problem 5(a), but the negative value is equally valid and gives -70.093 as an alternate answer for problem 5(a). However, we would normally ignore this negative answer, since in geometry, lengths are usually taken to be positive values only. The geometric mean arises quite naturally as the length of the segment which is perpendicular to the hypotenuse of a right triangle and which connects to the right-angle vertex. This "altitude" of the right triangle has length equal to the geometric mean of the two segments that make up the hypotenuse.

5.(b) 85, 153, and 221

5.(c) Let r denote the cube root of 11/12. The geometric means are -12r and -12r², or approximately -11.657 and -11.324.

6. Answer to #27 is in back of book (n = 119). Answer to #30 is n = 39. Answer to #32 is n = 25.

7. This is the exact same problem as S4, except with a "word problem" wrapper around it. The solution to S4 is available here.

8. Solutions to S6 and S7 are available here.

9. Answer to #5 is in back of book.

10. Solution to #14 is available here.

11.(a)

11.(b)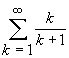

11.(c)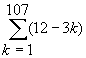

Other forms are possible for problem 11(c). For example, you may have written 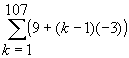, which is the same thing. Note that in either case, parentheses are required even though your textbook omits them for some strange reason. The rule of PEMDAS makes the parentheses necessary. In problem 11(b), parentheses are not required since the rule of PEMDAS says that each term k/(k + 1) will be evaluated before the additions that make up the sigma.

12.(a) DNE (or +¥ )

12.(b) 1

13.(a) DNE (or +¥ )

13.(b) DNE (or +¥ )

13.(c) -16,050