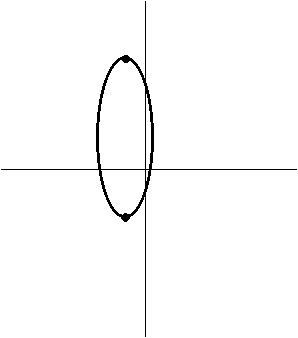|
1. |
Use the discriminant to identify each of the following conic sections. Show your work. |
|
|
(a) |
- xy + 15x + 4y = 17
|
|
|
(b) |
- 7,148,553,818x2 + 7,148,553,818y2 + 51,998x 7999y = 714,898
|
|
|
(c) |
- 66x2 72y2 + 8y = 21
|
|
|
(d) |
- x
2/4 + y2/9 = 0
|
|
|
(e) |
- 2y2 = 3x 7y
|
|
|
(f) |
- 2y2 = 3x2 7y
|
|
- 2.
|
- Sketch (c) and (e) from the previous question. Rough sketches are perfectly acceptable. For (c), label the coordinates of the center, foci, and y-intercepts, and sketch the asymptotes as dotted lines. For (e), label the coordinates of the vertex (or vertices), x-intercept(s), and y-intercept(s).
|
|
|
3. |
- Fill in the blanks below with the name of the proper conic section. No term is used more than once.
|
|
|
(a) |
- The set of points in a plane that are equidistant from a point F and a line (directrix) is called a(n) __________ .
|
|
|
(b) |
- The set of points in a plane that are equidistant from a single fixed point is called a(n) __________ .
|
|
|
(c) |
- The set of points P in a plane such that PF1 + PF2 (for foci F1 and F2) is a constant is called a(n) __________ .
|
|
|
(d) |
- The set of points P in a plane such that |PF1 PF2| (for foci F1 and F2) is a constant is called a(n) __________ .
|
|
|
4. |
- Write the equation for each of the following relations. For part (a) only, write the equation in Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 form; for the other parts, any form is acceptable.
|
|
|
(a) |
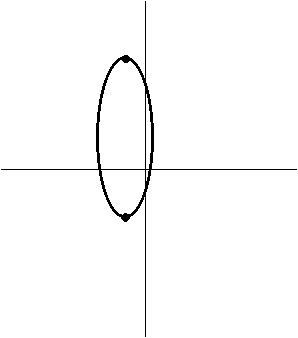
High and low points marked are at (3, 4) and (3, 8). Major axis is vertical, and focal radius is 4. |
|
|
(b) |
The axis of symmetry is the line y = 2, the x-intercept is at 11, and the point (1, 8) is on the curve. |
|
|
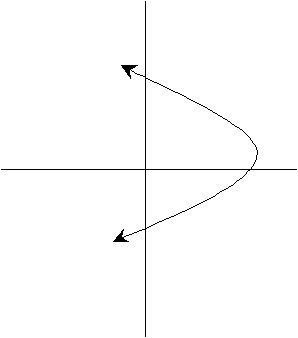
(c) |
Center is (4, 6); x-radius and y-radius are both 16. |
|
- 5.
|
- Use your calculator to plot problem 4(c) accurately. Raise your hand when you are ready to show it to your instructor. Do not worry if the last pixel at the left and right edge are skipped.
|
|
- 6.
|
- Solve the following system graphically (show your graphs clearly):
5x2 + 9y2 = 161
x2 4y = 4
|
|
- 7.
|
- Solve the system in #6 algebraically.
|
|
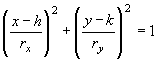 , c2 = a2 b2
, c2 = a2 b2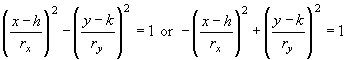 , c2 = a2 + b2, asymptote slopes ± b/a
, c2 = a2 + b2, asymptote slopes ± b/a