Algebra II / Mr. Hansen

Name: _____________________________

4/21/2000 Test on §§12-1 through 12-6, plus Binomial Theorem

 

Show all work
For full credit, show all work. You may use your calculator in any way that you wish, including study aids stored into your calculator's memory, but you must show sufficient work on your paper to demonstrate clearly that you understand the concepts. For example, if you assert that the number of ways of doing something is 6, you should provide a justification such as 4C2 = 6. An exception would be if the answer is obvious (e.g., the total number of equally likely outcomes of a fair die is clearly 6).

"Immunization"
If you claim immunization credit for a problem, write "IMMUNIZED" in the margin. Then I will know to look over your sample test and extra HW problems to see whether you qualify for lenient scoring.

1.

Compute (2a2 – 3b3)5. Simplify all terms fully.

 
2.
Write the 493rd term in the expansion of (6a – 2p8)797. Please do not simplify.

 
3.
Show that .

 
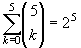4.
Compute the probability of drawing two hearts when

 

(a)
2 cards are drawn with replacement from a standard 52-card deck that is shuffled in between the draws

 

(b)
2 cards are drawn without replacement from a standard 52-card deck

 

(c)
5 cards are drawn without replacement from a standard 52-card deck (note: you must draw 2 hearts and 3 non-hearts, in any order)

 
5.
Compute each of the following. Show both the notation (e.g., nPr or nCr) and the numeric answer.

 

(a)
In how many ways can a committee of 5 sophomores be selected from a class of 73 sophomores?

 

(b)
In how many ways can a 7-character license plate be formed from the letters of the alphabet, the digits, and the special characters blank, hyphen, #, $, and © ? Assume that repeats are not allowed.

 

(c)
Answer part (b) assuming that repeated characters are allowed.

 
6.(a)
Let A be the event of rolling an even number (2, 4, or 6) with a fair die, and let B be the event that when a piece of buttered toast is tossed randomly into the air, it lands with the buttered side down. Give an estimate P(B) based on your personal experience: ____

 

(b)
Compute P(A) using the "or" rule.

 

(c)
Why is the "or" rule valid in part (b)?

 

(d)
Compute P(A Ç B) and explain what this means in English.

 

(e)
Explain why the method you used to compute part (d) is valid.

 

(f)
Compute P(~B) and explain what this means in English.

 

(g)
Compute P(A Ç ~B) and explain what this means in English.

 
7.
Approximately 4% of the people accused of whispering in chapel are actually innocent. If you randomly select 4 people from a large crowd of mostly whispering students, what is the probability that

 

(a)
all 4 are innocent?

 

(b)
all 4 are guilty?

 

(c)
at least 1 of the 4 is innocent?

 
8.
Wing and Prayer Aircraft Corporation manufactures a twin-engine plane. Laboratory tests indicate that the probability of any one engine failing during a particular flight is 0.03.

 

(a)

If the engines operate independently, what is the probability that both fail?

 

(b)

Flight records reveal that the probability of both engines failing during a particular flight is actually 0.006. What is the probability that the second engine will fail after the first has already failed?

 

(c)

Based on your answer to part (b), do the engines actually seem to operate independently? Why or why not?

 
9.
As always, work is required for this problem. Fifteen people try out for a baseball team. In how many different ways could the manager select

 

(a)

the pitcher and the catcher?

 

(b)

the three outfielders, after the pitcher and catcher have been selected? (Assume that RF, CF, and LF are treated as different positions requiring unique qualifications. In other words, we don’t simply select people to be "fielders.")

 

(c)

the First, Second, and Third Basemen and the Shortstop, after the pitcher, catcher, and three outfielders have been selected?