Algebra II / Andreoli, Graham, Hansen
January 2000 Practice Midterm Exam (2 hours)

Name: _____________________________

The purpose of this practice exam is to help you review by showing you the wording and types of problems on the actual exam. Although most of these practice problems are similar to real ones, not all types of problems are represented here. For example, you are expected to be familiar with all the field properties and may be asked to provide the justifications for the steps in a proof (e.g., writing Distrib. or Ident. ΄ ). You will not need to construct proofs from scratch.

No notes or scratch paper
You cannot use notes or scratch paper on the actual exam; ample room to write will be provided. However, to save paper, the practice exam does not include such space for writing. Use your own paper to write out the practice exam answers.

Calculator
You may use your calculator on all parts of the exam. However, since your work is what will be graded, not your answer, in most cases you should use your calculator only to check your work. Decimal approximations are acceptable only when the problem says "round to ____ places" or "round to the nearest _____ ." Example: If the problem says to simplify (486)1/5, you should show work as (2 · 243)1/5 = 21/5 · 2431/5 = 3 · 21/5. A decimal answer in this case would receive no credit.

Simplifying
The word "simplify" means to leave everything in simplest form (e.g., write 2Ö 2 instead of Ö 8 in your final answer), with no radicals in the denominator, and in a + bi format in the case of complex numbers.

Word problems
For word problems, show the setup and indicate your solution method in a clear, sequential manner. Answer the question posed, and include units of measure when appropriate.

1.

Simplify.

(a)

(b)

(c)

(3y – 11) (2y + 6)

(d)
(w – 4) (w2 + 2w – 3)
2.
Solve and graph the solution set: |2x – 3.5| ³ 2.
3.
Simplify:
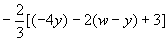
4.
Solve for z:
|5 – 3z| = 2
5.
Assuming that bx + cy Ή 0, solve the following equation for x:
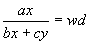
6.
Solve and graph the solution set:
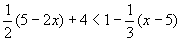
7.
Solve for q:
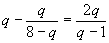
8.
If 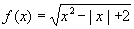and 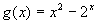, find f(g(f(–2)) + f(g(2))).
9.
Find the slope-intercept form of the line that passes through (2, –17) and is parallel to the line that passes through (–5, –4) and (–7, –8).
10.
Graph the following system of inequalities and shade the solution set:
3x + 2y < –2
–2x + 5y ³ 10
x + y £ –1
11.
In problem 10, suppose that C = 15x + 2.77y is the linear cost function associated with variables x and y in a linear programming problem. Compute the only possible ordered pair (x, y) at which C could attain a maximum or minimum value.
12.
Solve the following system of equations by any method. For full credit, you must show all work. Check your answer with your calculator.
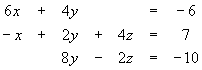
13.
Perform the following division by long or synthetic division. Write your answer as a polynomial plus a remainder (standard mixed-number form):
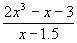
14.
Add and simplify:

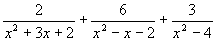
15.(a)

Complete the square to transform the parabola y = –2x2 – 6x + 3 to vertex form.

(b)
Sketch the graph, labeling the coordinates of the vertex and x- and y-intercepts.

(c)
What is the equation of the axis of symmetry?
16.
Simplify:

(a)
(16x)–1/2 (3x)2

(b)

17.(a)

If x + 2 is a factor of the polynomial P(x) = 2x3 + 11x2 + 16x + 4, find all the real roots of P.

(b)
State P(x) in fully factored form.
18.
Simplify, assuming that all radicals denote real numbers:

(a)

(b)
19.
Simplify and express in "a + bi" form:
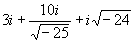
20.
Let 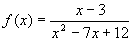. Graph f, labeling any asymptotes, removable discontinuities, and intercepts.
21.
Simplify completely, using only positive exponents:

(a)

(b)
22.
A triangular plot of land has base 30 meters and height 15 meters. If the base and height are both increased by the same number of meters, the area would be tripled. Use a quadratic equation to find by how many meters each dimension would need to be increased.
23.
A soccer ball is shot upward from a cannon mounted at a height of 10 feet. The height of the ball is therefore 10 feet at time 0 seconds. At time 2.5 seconds, the ball has a height of 175 feet, and at time 4.5 seconds, the ball has a height of 163 feet.

(a)
Find the particular quadratic equation that gives the height of the ball as a function of time t. (You must show your setup, but you can use your calculator to solve the messy system of linear equations that results.)

(b)
Compute the hang time of the ball to the nearest thousandth of a second.

(c)
What is the muzzle velocity of the ball in feet per second? (Hint: This is given by the coefficient of the linear term of the equation you found in part (a).) Is this faster or slower than 60 mph?
24.
Suppose that the mass of a scale model of the Titanic varies inversely with the cube of the number of times sound can travel from one end of the model to the other in a second. James Cameron’s first Titanic model had a mass (let’s say) of 4000 kg, and an echo sent from one end of the model to the other could make 18 round trips in one second. A larger model is now constructed, such that sound can make only 7 round trips from one end to the other in one second. Assume that temperature is constant.

(a)
Find the particular equation that gives mass as a function of number of round trips of sound per second.

(b)
To the nearest kg, what is the mass of the larger model (i.e., the one for which sound can make only 7 round trips in a second)?
25.
Find three consecutive positive integers such that when 10 times the largest is subtracted from the square of the second largest, the result is 6 less than quadruple the smallest.