(rev. 9/5/2000)

Mathematicians use the symbol S (the Greek capital letter "sigma") as a shorthand to indicate that a series of values should be added up. Sometimes the number of values to be added is very large, or even infinite, which explains why this shorthand is so useful.

For example, 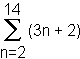is math shorthand that can be understood as follows:

The index, or changing variable, is n. We can tell that the starting value for n is 2, and the ending value for n is 14. We read the expression 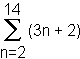as, "the summation of the quantity 3n + 2 as n goes from 2 through 14." When n = 2, the quantity in parentheses (the summand, or term) is 8. When n = 3, the summand is 11. Plugging in different values for n, we can see that the answer is 8 + 11 + 14 + 17 + 20 + 23 + 26 + 29 + 32 + 35 + 38 + 41 + 44, which simplifies to 338.

In Algebra II, students learn a formula for computing summations involving linear summands. In this case, the summand 3n + 2 is linear, so you can simply multiply the number of terms by the average of the first and last terms. Try it! Here, there are 13 terms (2 through 14), and the average of the first and last would be (8+44)/2, which is 26. If you multiply 13 times 26, you get 338. Amazing! Remember, this trick works only when the terms are linear.

You could challenge a friend or a sibling to a race to add up the numbers 1 + 2 + 3 + 4 + ... + 138 + 139 + 140, i.e., the first 140 positive integers. No matter how fast the other person is with punching buttons on a calculator, you will win this contest, since you know the trick. Multiply the number of terms (140) by the average of the first and last to get the answer. Let’s see, the average of the first and last would be (1+140)/2, or 70.5. Multiply 140 times 70.5 to get 9870. You’re finished!