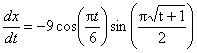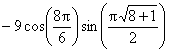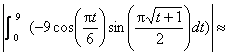|
|
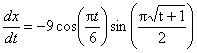 , , 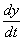 is not given is not given
[At] t = 9, particle reaches final
position at D [on x-axis.]
|
|
|
|
|
(a)
|
Note: it is important to
consider 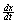 before before
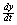 . .
|
|
|
At point C, 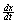 is not positive. This
is reached at by inspection of the graph of is not positive. This
is reached at by inspection of the graph of 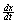 . This graph shows that for all values of t . This graph shows that for all values of t 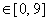 , , 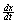 is not greater than zero. is not greater than zero.
 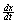 is not positive at
point C. is not positive at
point C.
|
|
|
|
|
|
At point C, 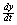 is also not positive
at point C. Because is also not positive
at point C. Because 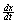 is not greater than
zero, we know that the particle cannot “trace” back upon itself. is not greater than
zero, we know that the particle cannot “trace” back upon itself.
 , because the particle is decreasing in y-magnitude from C , because the particle is decreasing in y-magnitude from C 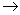 D in general, we
know that D in general, we
know that 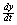 cannot be positive. cannot be positive.
|
|
|
|
|
(b)
|
For 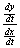 to be undefined, to be undefined, 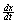 must = 0. must = 0.  Consider Consider 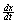 = 0. = 0.
From the graph of 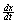 , , 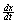 = 0 only at t = 3 on = 0 only at t = 3 on 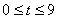 . .  At point B, t = 3. At point B, t = 3.
|
|
|
|
|
(c)
|
t =
8 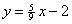 We know We know 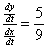 (from slope of
tangent line). (from slope of
tangent line).
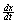 @ t = 8 is @ t = 8 is 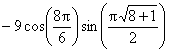  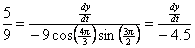
 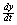 = =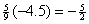
|
|
|
|
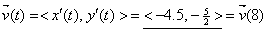
speed = 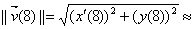 5.148 units/time unit 5.148 units/time unit
|
|
|
|
|
(d)
|
To find the distance
between A & D, we are only concerned with x values.
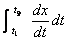 = accumulated rate
of change of x = distance traveled
between t1 and t9 = accumulated rate
of change of x = distance traveled
between t1 and t9
 Distance between A and D = Distance between A and D = 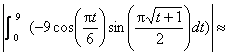 39.255 units 39.255 units
Time it takes for the particle to get from A to D is from t = 0 to t =9.
At t = 0, the particle is at A. At t = 9, the particle is at D.
|
|
|
|
|
|
Commentary by Mr. Hansen
|
|
|
|
|
(a)
|
Depending on how the rubric
is written, Isaac’s explanation may not be permitted. You cannot give as a
justification for the sign of an expression the observation that the graph
does not appear to have any positive values. Remember, you are not allowed to
“reason from a graph.” Safer explanation is to look at the two relevant
intervals of t values.
First, for 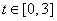 , , 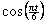 goes from cos 0 to cos goes from cos 0 to cos 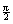 (hence always (hence always 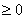 , and 0 only at t
= 3), while , and 0 only at t
= 3), while 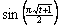 goes from sin goes from sin 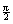 to sin to sin 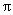 (hence always (hence always 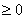 , and 0 only at t
= 3). [Reasoning like this is fine, by basic properties of trig functions.] , and 0 only at t
= 3). [Reasoning like this is fine, by basic properties of trig functions.]
Second, for 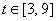 , , 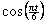 goes from cos goes from cos 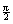 to cos to cos 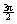 (hence always (hence always 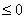 , and 0 only at t
= 3, 9), while , and 0 only at t
= 3, 9), while 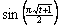 goes from sin goes from sin 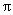 to to 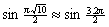 (hence always (hence always 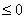 , and 0 only at t
= 3). , and 0 only at t
= 3).
Therefore, for all 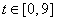 , the given expression for , the given expression for 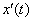 is the product of –9
and two factors that never have a negative product. We conclude that is the product of –9
and two factors that never have a negative product. We conclude that 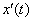 is never positive.
Moreover, the product is 0 only at t
= 3 and t = 9. Thus is never positive.
Moreover, the product is 0 only at t
= 3 and t = 9. Thus 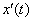 is not positive
at C. is not positive
at C.
As for 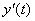 , we know , we know 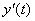 has the same sign as has the same sign as
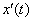 at point C, since at point C, since 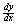 is positive there by
inspection (slope of tangent line). Therefore is positive there by
inspection (slope of tangent line). Therefore 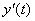 is also not
positive at C. [Later on, after we know that point B corresponds to t = 3, we can say that is also not
positive at C. [Later on, after we know that point B corresponds to t = 3, we can say that 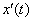 and and 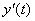 are both negative at
C. However, we have answered the questions posed, and we need to move on.] are both negative at
C. However, we have answered the questions posed, and we need to move on.]
[Note: This is a lot of work for what cannot possibly be more than 2 points
out of 9. Even though Isaac may not have earned both points, his method is a better
strategy, since it is time-efficient.]
|
|
|
|
|
(b)
|
Since both x(t) and y(t) are differentiable
[given], we know that the slope, 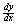 , is undefined only if , is undefined only if 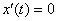 . Isaac omitted only the first observation, and a picky rubric
would find fault with that, since one cannot assume in all cases that
undefined slope means denominator is zero. . Isaac omitted only the first observation, and a picky rubric
would find fault with that, since one cannot assume in all cases that
undefined slope means denominator is zero.
Use of root-finder is permitted, and the only root on [0, 9] is at t = 3. Assuming that
part (b) is worth 2 points, Isaac’s solution would probably be 1 point out of
2.
|
|
|
|
|
(c)
|
Full points, probably 3 out
of 3.
|
|
|
|
|
(d)
|
Full points, probably 2 out
of 2. Note that a mere setup and answer would suffice:
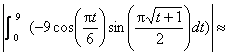 39.255 units 39.255 units
|
|
|
|
|
|
Final score for Isaac: 7 or
8 points out of 9, depending on how picky the rubric is. Either way, he is safely
in “AP 5” territory. Bravo!
|