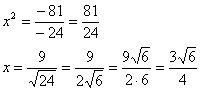|
A.
|
Given two congruent
circles, A and B, each with radius of 10, and given that the common internal
tangent has length 7, find AB.
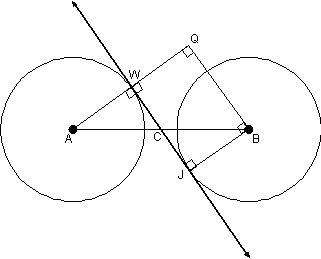
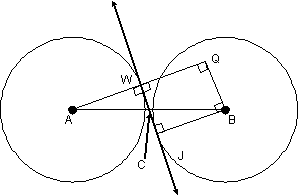
Given: AW = BJ = 10, WJ = 7, 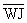 internally tangent internally tangent
Find: AB
Since 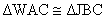 by AAS, we know WC =
JC and AC = BC by CPCTC. Therefore, WC = JC = 3.5. by AAS, we know WC =
JC and AC = BC by CPCTC. Therefore, WC = JC = 3.5.
By Pythag. Thm., AC = BC = 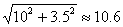
Therefore, AB = 2AC = 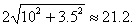
Better solution method (tip of the hat
to Kealan H.):
Since WQ = JB = 10, AQ = 20. For the same reason, QB = WJ = 7. Therefore, by Pythag. Thm., AB = 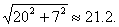
Note: The diagram above is not to scale. In fact, point Q
cannot possibly be shown correctly above! Remember, BQWJ is a rectangle,
which means that BQ = WJ = 7, and therefore Q must be inside circle B, whose radius is 10. Here is a more accurate
diagram, although it has the disadvantage of making point C hard to label:
|
|
B.
|
Given two externally
tangent circles whose radii are in a 3:2 ratio, find the radii if the length
of a common external tangent is 9.
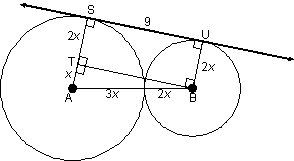
Solution: Let 3x
and 2x represent the radii as
marked. In other words, let 3x = rA, and
let 2x = rB. By rect. props., TB = SU = 9. Then, by Pythag.
Thm.,
9 = 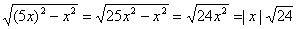 . Since x is a
length, the absolute value bars can be omitted, and we have . Since x is a
length, the absolute value bars can be omitted, and we have 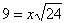 , from which we obtain , from which we obtain
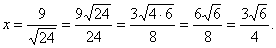 Therefore, rA =
3x = Therefore, rA =
3x = 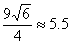 , and , and 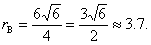
Better solution method (tip of the hat
to Abbott B.):
By Pythag. Thm., 92 + x2
= (5x)2, so that x2 – (5x)2 = –92. We have
–24x2 = –81
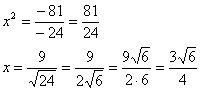
Therefore, rA
= 3x = 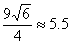 , and , and 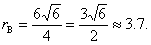
|