Geometry / Mr. Hansen 3/2/2009

Name: ________________________

Proof of the “HUGH” Theorem

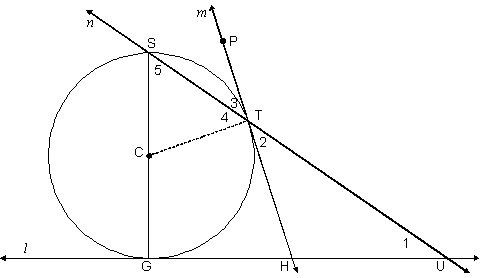
Given: l, m tangent to circle C at G and T, respectively Prove: HU = GH
1. Circle C	| 1. Given
2. Lines l, m tangent at G and T, resp.	| 2. Given
3.	| 3. Postulate: radius to tangent
4. Construct	| 4. Two pts. det. a line
5.	| 5. Same as (3)
6. comp.	| 6. Def. comp.
7.	| 7. Radii of same circle are
8.	| 8. ITT
9. comp.	| 9. Subst. (8, 6)
10.	| 10. Vert.
11. comp.	| 11. Subst. (10, 9)
12. is a rt.	| 12. Def. rt. (from 3)
13. comp.	| 13. Non-rt. in a rt. are comp.
14.	| 14. Comps. of same are (from 11, 13)
15. HU = HT	| 15. ITT
16. HT = GH	| 16. TTT [a.k.a. “Ice Cream Cone Theorem”]
17. HU = GH	| 17. Trans. (15, 16)
(Q.E.D.)
Faster alternate method (does not require constructing auxiliary segment):
1. Circle C	| 1. Given
2. Lines l, m tangent at G and T, resp.	| 2. Given
3. Left arc SG = arc STG = 180°	| 3. Diag., def. semicircle
4. arc ST + arc TG = 180°	| 4. Arc add.
5. arc TG = 180° – arc ST	| 5. Alg.
6.	| 6. Half SAD [Half D]
7.	| 7. Subst. (3, 5, 6)
8.	| 8. Alg. [simplif. of 7]
9.	| 9. Half SAD [Half A]
10.	| 10. Vert
11.	| 11. Trans. (8, 9, 10)
12. HU = HT	| 12. ITT
13. HT = GH	| 13. TTT
14. HU = GH	| 14. Trans. (12, 13)
(Q.E.D.)