|
16.
|
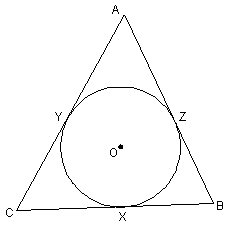
|
Given: AB + BC + CA = 38
AB = 14
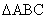 is isosceles is isosceles
pts. of tangency
X, Y, and Z
Find: XC, BX
|
|
|
Since we do not know in what way 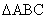 is isosceles, we
must consider cases. is isosceles, we
must consider cases.
|
|
|
Case I: Suppose that AC
= BC.
|
|
|
By TTT, XC = YC.
Since AC = BC, we know AY = BX by subtraction.
By TTT, BZ = BX and AZ = AY.
By transitive prop., AZ = BZ.
Since AB = 14, AZ = BZ = 7.
Since AZ = BZ = AY = BX = 7, the sum of their lengths is 28.
Since perim. of 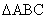 is 38, YC = XC = 5. is 38, YC = XC = 5.
Summary of Case I: XC = 5, BX = 7.
|
|
|
Case II: Suppose that AC
= AB.
|
|
|
Let x =
AY = AZ.
Since AB = 14, BZ = 14 – x.
By TTT, BX = 14 – x also.
If we add up AY + AZ + BZ + BX, we get x
+ x + (14 – x) + (14 – x) = 28.
Since perim. of 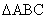 is 38, YC = XC = 5. is 38, YC = XC = 5.
Since AB = AC = 14, AY = AZ = 9.
Therefore, BZ = 5, and BX = 5 also.
Summary of Case II: XC = 5, BX = 5.
|
|
|
Case III: Suppose that AB
= BC.
|
|
|
Since AB = 14, BC = 14 also.
Since perim. = 38, AC = 10.
Follow the “walk-around” procedure that we learned.
First, let y = XC.
By TTT, YC = y also.
BX must be 14 – y, and by TTT, BZ =
14 – y also.
Since AB = 14, AZ = y.
By TTT, AY = y also.
Now we have perim. = XC + BX + BZ + AZ + AY + YC
=
y + (14 – y) + (14 – y) + y + y + y = 38
By algebra, 28 + 2y = 38 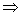 2y = 10 2y = 10 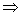 y = 5. y = 5.
Finally, if y = XC = 5, then BX =
9.
Summary of Case III: XC = 5, BX = 9.
|
|
(a)
|
Regardless of how the sides of the isosceles triangle are paired, XC =
5.
|
|
(b)
|
Depending on which case is in effect, we could have BX = 7, BX = 5, or
BX = 9.
|
|
|
Whew! That was a lot of fun, and I hope you enjoyed following those steps.
On a test, you would not have to write out all those steps with explanation;
you could simply draw the diagram 3 times and mark them up quickly.
However, there is an even faster way. Try this alternate method:
|
|
(a)
|
Let u = AY = AZ. (The two
lengths are equal by TTT.)
Let v = BZ = BX. (TTT again.)
Let w = XC = YC. (TTT again.)
We know u + v = AZ + BZ = AB = 14 (given).
We also know that perim. = 2u + 2v + 2w = 38. Simplified, this is u + v + w = 19.
However, since u + v = 14, we can substitute to get 14 + w = 19.
Therefore, w = XC = 5 in all
situations.
|
|
(b)
|
We have 3 cases to consider.
Case I: If AC = BC, then
since AB = 14, AC = BC = 12 so that perim. = 38.
Therefore, since BC = 12, BX = 7.
Case II: If AC = AB, then both
AB and AC must be 14. Since perim. = 38, BC = 10.
Therefore, BX = 5.
Case III: If AB = BC, then
both AB and BC must be 14. Since BC = 14, BX = 9.
|
