Solutions
for Modules 11–15
© 2003 by David C. Garlock
[Web version ed. by EMH
5/20/2003]
Module 11. Finding Solutions to ax+by=1
1.
107
= 24 × 4 + 11
24
= 11 × 2 + 2
11
= 2 × 5 + 1
2
= 1 × 2.
Substituting the expression for 2 obtained from the third-to-last equation into the 2 in the second-to-last equation, we obtain:
11
– 2 × 5 = 1
11
– (24 – 11 × 2) × 5 = 1
(11
× 11) – (24 × 5) = 1
Substituting the expression for 11
obtained from the first equation into the last one just derived, we obtain:
(11
× 11) – (24 × 5) = 1
((107
– 24 × 4) × 11) – (24 × 5) = 1
107
× 11 – 24 × (–44 – 5) =1
107
× 11 – 24 × (–49) = 1
Therefore, a solution to the equation 107x + 24y = 1 is x = 11 and y = –49.
2.
As we found in Module 9, Problem 4,
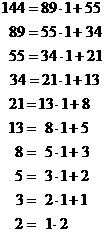
Notice that the quotients are all 1, except for the last one, which is 2.
From the second- and third-to-last equations, we obtain:
3
– 2 = 1
3 – (5 – 3) =
1
3 × 2 – 5 × 1 =
1.
Now from the equation involving 8, 5 and 3, we obtain:
3
× 2 – 5 × 1 =
1
(8
– 5) × 2 – 5 × 1 = 1
8× 2 – 5 × 3 =
1.
From the equation involving 13, 8 and 5, we obtain:
8× 2 – 5 × 3 =
1
8× 2 – (13 – 8) × 3 = 1
8
× 5 – 13 × 3 =
1
Continuing with substitutions and regroupings:
(21
– 13) × 5 – 13 × 3 = 1
21
× 5 – 13 × 8 =
1
21
× 5 – (34 – 21)
× 8 = 1
21
× 13 – 34 × 8 =
1
(55
– 34) × 13 – 34 × 8 = 1
55
× 13 – 34 × 21 =
1
55
× 13 – (89 –
55) × 21 = 1
55
× 34 – 89 × 21 =
1
(144
– 89) × 34 – 89 × 21 = 1
144
× 34 – 89 × 55 =
1.
Therefore, a solution to the equation 144x + 89y =
1 is
x = 34 and y = –55.
Suppose that we replaced the last equation in
2
= 1 × 1 + 1
1 = 1 × 1.
If we begin the substitution process with these equations, we obtain a similar but different set of relationships:
2
× 1 – 1 × 1 = 1
2
× 1 – (3 –2) × 1 = 1
2
× 2 – 3 × 1 =
1
(5
– 3) × 2 – 3 × 1 = 1
5
× 2 – 3 × 3 =
1.
5
× 2 – (8 – 5) × 3 = 1
5
× 5 – 8 × 3 =
1
(13
– 8) × 5 – 8 × 3 = 1
13
× 5 – 8 × 8 =
1
13
× 5 – (21 –13) × 8 = 1
13
× 13 – 21 × 8 =
1
(34
– 21) × 13 – 21 × 8 = 1
34
× 13 – 21 × 21 =
1
34
× 13 – (55 –
34) × 21 = 1
34
× 34 – 55 × 21 =
1
(89
– 55) × 34 – 55 × 21 = 1
89
× 34 – 55 × 55 =
1
89
× 34 – (144 –
89) × 55 = 1
89
× 89 – 144 ×
55 = 1.
This gives us another solution to the equation 144x + 89y
= 1, which
is
x = –55 and
y = 89.
These equations suggest the following two identities among successive Fibonacci numbers (where Fn represents the nth Fibonacci number):
These formulas are easily proved using induction.
3.
a = b×q1 + r1
b = r1×q2 + r2
r1 = r2×q3 + r3
.
. . .
rn–2 = rn–1×qn + rn
rn–1 = rn×qn+1.
From Module 9, rn is the gcd
of a
and b. For convenience, we will
define
r0 = b and r–1 = a. We will prove by induction
that it is possible to express rn as a linear combination of rn–k
and rn–(k+1) for 1 < k < n. The second-to-last equation gives and expression for rn
in terms of rn–1
and rn–2,
so the induction hypothesis holds for k=1. Now
suppose there is an expression for rn as a linear combination of rn–(k–1) and rn–k for 1 < k < n, say rn = s × rn–(k–1) + t × rn–k. Since k < n, one of the equations in
rn = s× rn–(k–1) + t× rn–k = s × (rn–(k+1) – rn–k×qn–(k–1)) + t × rn–k = s × rn–(k+1) + (t – qn–(k–1))× rn–k. This is the desired
linear expression of rn
in terms of rn–k and rn–(k+1), which completes the
induction proof.
4.
Suppose (a,b) = c > 1, 
and 
. Let (x,y) be a solution to the equation ax+by = c. Dividing by c,
one obtains a0x+b0y = 1. Conversely, if (x,y)
is a solution to the equation a0x+b0y = 1, one can multiply by c
to obtain ax+by
= c.
5.
The congruence 
is equivalent to the
equation 
43
= 19 × 3 + 4
19
= 4 × 4 + 3
4
= 3 × 1 + 1
3
= 1 × 3
There is no need for substitution because the first
equation gives the desired solution directly: x = –3
and y = 1.
6.
The equation in integers corresponding to the
congruence 
is 
. A solution by inspection is 
.
17
= 5 × 3 + 2
5
= 2 × 2 + 1
2
= 1 × 2
Substituting 17 – 5 × 3 for one of the 2s in the middle equation gives:
5 = 2 × (17 – 5×3) + 1 or 5 × 7 – 17 × 2 = 1, which is the same solution.
Module 12. Gaussian Integers
The set of complex numbers a+bi such that a and b are integers is called the set of Gaussian integers. The domain of Gaussian integers is denoted Z[i].
1.
Let 
Z[i].
Then 
Z
s.t. 
and 
. Thus, 
Z[i]. Therefore, Z[i] is closed
with respect to multiplication.
2. (5 + 7i)(3 + 2i) = 1 + 31i.
3. (2 + 3i)(2 – 3i) = 13. (4 + 7i)(4
– 7i) = 65. (a +
bi)(a – bi) = a2 +
b2.
4. There is no way to extend the ordering for integers to Gaussian integers. For regardless of whether i is positive or negative, its square (–1) would then be positive, which of course is inconsistent with the ordering of the integers.
5.
The “absolute value” of a Gaussian integer a+bi can be
defined as 
. If the Gaussian integers are plotted on a coordinate
system, then the quantity represents the
distance of the Gaussian integer from the origin. In the case of a rational
integer a (i.e., b = 0),
the definition is the same as the definition of the absolute value of the
integer a.
6.
2 = (1 + i)(1 – i).
5 = (2 + i)(2 – i).
13 = (2 + 3i)(2
– 3i).
3, 7, and 11
cannot be factored in Z[i]. The prime 2 and
odd primes of the form 4n + 1 can
be factored in Z[i].
Rational primes of the form 4n + 3
remain prime in Z[i].
7.
One cannot find a Gaussian integer with two
different Gaussian prime factorizations, for as we will prove in Module 30, Z[i] is a unique
factorization domain.
8. 47 – i = (1 – i)(2 – i)(2 + 3i)(4 + i).
Module 13. More Modular Arithmetic
1.
a. a – a
= 0 = 0 × m Þ a º a (mod m).
b. a º b (mod m) Þ m½b – a Þ m½a – b Þ b º
a (mod m).
c. a º b (mod m) Þ m½b – a. b º c (mod m) Þ m½c – b. Because
c – a = (c – b) +(b – a),
m½c – a. Therefore,
a º c (mod m).
2.
If a
is an integer, then by the division algorithm $ q, a' s.t. a = mq+ a' and
0 £ a' < m. Since a – a' = mq, this shows that a
º a' (mod m),
for if there were another integer a"
congruent to a mod m and satisfying 0 £ a" < m, we would have a"
º a' (mod m),
which means m½ a" – a',
and –m < – a'
< m. But the only integer between –m
and m divisible by m is 0, so a"
= a'. This shows that a' is unique.
3.
If a º a' (mod m)
and b º b'
(mod m), then m½a – a' and m½b – b' Þ
m½(a+b)
–
(a'+ b') Þ
a+b º a'+b' (mod m).
For multiplication, m½a – a' Þ
m½ab – a'b and m½b – b' Þ m½a'b
–
a'b'. Summing again, we have m½ab – a'b', which implies
ab º a'b' (mod m).
4.
From the preceding problem, if a º
b (mod m),
then for any exponent n
and any constant k, 
. Adding together these terms as building blocks, it is
possible to construct any polynomial with integer coefficients. Therefore, for
any polynomial f(x)
with integer coefficients, a º b (mod m) Þ f(a) º
f(b) (mod m).
5.
ac
º bc (mod m) Þ
m½bc – ac
Þ m½(b – a)c. If (c,m) =1, then by the fundamental
theorem of arithmetic m½(b – a)
Þ a º
b (mod m).
6.
If (a,m) = 1, then since there are only m distinct residues mod m,
and since a power of a
can never be divisible by m,
among the m integers a, a2, … am,
there must be at least one pair of distinct exponents k
and j for which ak
and aj
are congruent mod m and not congruent to
0
mod m. If we set
n = k – j, we then have an º 1(mod m).
7. The values of 2n in Z13 are, successively, 2, 4, 8, 3, 6, 12, 11, 9, 5, 10, 7 and 1. All 12 of the possible values in Z13 (other than 0) are generated, with 1 being the last of these. The value of 12, or –1, is reached half way through the process, i.e., 26 º –1. Given that 212 º 1 and (–1)2 º 1, this would have to be the case. Accordingly, the last 6 values of 2n are the negatives of the first 6 values.
8. The values of the successive powers of 5 in Z13 are 5, 12, 8 and 1. After that, the pattern repeats. The powers of 3 in Z13 are 3, 9, and 1. The pattern again repeats, this time in a cycle of 3.
9. The powers of 2 in Z17 are 2, 4, 8, 16, 15, 13, 9 and 1. This accounts for half of the non-zero residues mod 17. Note that all of the numbers obtained are perfect squares mod 17. The powers of 3 in Z17, in order, are 3, 9, 10, 13, 5, 15, 11, 16, 14, 8, 7, 4, 12, 2, 6 and 1. These are all of the distinct non-zero residues mod 17.
10. Each of the numbers 1, 3, 5 and 7 satisfies the congruence x2 – 1 º 0 (mod 8). Recall Problem 8 of Module 3, in which we showed that the square of any odd number is 1 more than a multiple of 8.
11. A
number k is a unit mod m iff 
. This is equivalent to 
. From what we proved in Module 10, this is equivalent to (k,m) = 1.
12. The
product of two units is always a unit. This follows from the preceding
exercise, or more directly from the fact that if 
and 
then
.
13. The group of units mod p for any prime p is cyclic.
14. The group of units mod m is cyclic if m is 2, 4, a power of an odd prime, or twice a power of an odd prime. We will prove these results in Modules 24 and 25.
15.
|
Exponent |
Power of 2 |
|
|
|
|
1 |
2 |
|
2 |
4 |
|
3 |
8 |
|
4 |
3 |
|
5 |
6 |
|
6 |
12 |
|
7 |
11 |
|
8 |
9 |
|
9 |
5 |
|
10 |
10 |
|
11 |
7 |
|
12 |
1 |
5 º 29 mod 13. 9 º 28 mod 13. 5 × 9 º 29 × 28 º 217 º 212 × 25 º 6 (mod 13). Stated in terms of logarithms, log25 = 9. log29 = 8. 9+8 = 17 º 5 (mod 12). log2–1(5) = 6. You compute exponents and logarithms mod 12 because 212 º 1 (mod 13), so the powers of 2 repeat with a period of 12.
Module 14. Continued Fractions
1.
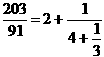. The convergents are 2, 
and 
. Note that
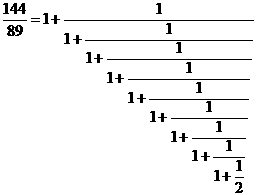. The convergents are the ratios of
successive Fibonacci numbers: 
.
2.
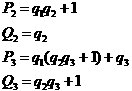
3.
The expressions are 
. The expressions are valid for n = 2
from what we proved in the preceding problem. Now suppose the expression are valid for n
as above. We want to use this to show that 
. The induction hypothesis is that expressions for
Pn+1 and Qn+1
are valid for any value of qn+1. Hence, we can replace qn+1 by 
. But doing this gives expressions for Cn+2, because
if we replace qn+1 by
in the expression 
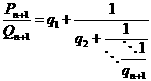, we obtain 
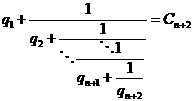. Therefore, from this substitution, we have:
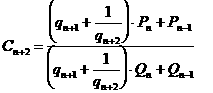
and multiplying numerator and denominator by qn+2 yields:
This shows that , which completes the proof by induction.
4.
For n =1, P1×Q2 – P2×Q1 = q1q2 – (q1q2+1)×1 = –1.
Now suppose that for some value of n, Pn×Qn+1 – Pn+1×Qn = (–1)n. Then
Pn+1×Qn+2 – Pn+2×Qn+1 = Pn+1× (qn+2Qn+1 + Qn) –
(qn+2Pn+1 + Pn) × Qn+1 = Pn+1× Qn – Pn × Qn+1
= –(–1)n = (–1)n+1.
Module 15. Polynomial Domains
1.
If qÎQ,
q¹0, then for any polynomial 
, if we define 
and 
, then we have 
, which shows that q|f(x). The coefficients of g(x) are all rational because the
coefficients of f(x) are rational and q is rational and not equal to 0.
2.
Let 
and 
. Define the monomial c(x) as c0xn–m where c0
is defined by 
. Then b(x)c(x) has as
its leading term anxn,
which is the same as the leading coefficient of a(x). Therefore, a(x) – b(x)c(x) is either of degree less than n or is the zero polynomial.
3.
We will use complete induction. Using the
notation of the previous problem, we hold the degree of the polynomial b(x) fixed
at m and proceed by induction
on the degree n of a(x). If n < m, we can take q(x) = 0 and r(x) = a(x). If n = m, then from the preceding
problem, the polynomial a(x) – b(x)c(x) has
the required characterisitcs for r(x). Now suppose the division
algorithm works for any degree of a polynomial up to n
and we want to show it works where the degree of a(x) is n+1. Once
again, we can apply the preceding problem to define 
and c(x) = c0xn+1–m, so that a(x) – b(x)c(x) is either of degree less than n+1 or is the zero polynomial. If a(x) – b(x)c(x) is
either of degree less than m or
is the zero polynomial, we have found our desired remainder polynomial. If not,
we can define a'(x) = a(x) – b(x)c(x). Since
a'(x) is a polynomial of degree at most n,
we can apply the induction hypothesis and find polynomials q'(x) and r(x) such that a'(x) º b(x)q'(x) + r(x), where
deg r(x) < deg b(x) or r(x) = 0. If we now define q(x) = c(x)
+ q'(x), we have a(x) º b(x)q(x) + r(x) and
either r(x)=0 or deg r(x) < deg b(x).