Solutions for Modules 6–10
© 2003 by David C. Garlock
[Web version ed. by EMH 5/12/2003]

Module 6. Prime Numbers and Their Distribution

1. Suppose the set of integers greater than 1 that have no prime divisors is not the empty set. Then by the well-ordering principle, that set has a smallest element. Say that number is n . If n is prime, then it has itself as a prime divisor, since every integer divides itself, so n cannot be prime. Therefore n can be factored into two smaller integers a and b: . Because a and b are each smaller than n, each has a prime factor (n was the smallest integer without a prime factor). But any prime factor of a or b is also a prime factor of n, which contradicts that n has no prime divisor. So the set of integers with no prime divisor is empty.

2. Suppose the set of integers greater than 1 that have no prime factorization is not the empty set. Then by the well-ordering principle, that set has a smallest element. Say that number is n . If n is prime, then it s prime factorization is simply the number n, so n cannot be prime. Therefore n can be factored into two smaller integers a and b: . Because a and b are each smaller than n, each has a prime factorization (n was the smallest integer without a prime factorization). So the product of the prime factorizations of a and b constitutes a prime factorization of n, which contradicts that n has no prime factorization. So the set of integers with no prime factorization is empty.

3. If m is positive and composite then there are positive integers a and b such that m = ab. Either a or b must be less than or equal to , for otherwise their product would exceed m. Say . From Problem 1, a has a prime factor and from Problem 3 of Module 3, that factor cannot exceed a. That prime factor of a is also a prime factor less of m, which completes the proof.

4. , so you need to check for prime factors up to 140. The reward comes near the end: 19,177 = 127 · 151.

5.  2×3×5×7×11×13 + 1 = 30,031 = 59×509.

6. Any number N that is a product of primes plus 1 has a prime divisor (which may be N itself) that differs from any of the primes in the product. For any prime that enters into the product divides the product so it cannot divide N. This proves that there are infinitely many prime numbers, since if there were only finitely many, we could set N equal to their product plus 1 and find another prime not in the product, contradicting the assumption that the product is divisible by every prime.

7. The value of n² – n + 41 is indeed prime for the first 40 positive integer values of n, which is rather remarkable, but the value of the expression for n = 41 is simply 41² = 1681, which obviously is not prime. The expression n² – 79n + 1601 generates primes for its first 79 integer values, but these are the same primes generated by n² – n + 41, as can be seen by substituting n+40 for n in the first equation.

8. In order for a polynomial to generate a prime value for n = 0, its constant term must be a prime; say the constant term is p. If one sets
n = kp for different integer values of k, the value of must always be divisible by p, since every term of is divisible by p. If is always prime, then must be equal to p for every value of k. But this is impossible, since a polynomial of degree m can take on a given value at most m times (for otherwise the polynomial would have more than m roots). Therefore, no polynomial can generate a prime for every value of n.

9. n!+2 is divisible by 2, n!+3 is divisible by 3, n!+4 is divisible by 4… , n!+n is divisible by n.

10. The first sequence of 10 or more consecutive composite numbers is
114 … 126.

11.

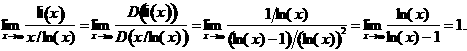
Module 7. Exploration

1. .

2. . The factorization is unique, if one does not consider factorizations different if they have the same primes in a different order.

3. The domain 3Z+1 is closed under multiplication because 3Z+1. These numbers are all prime in 3Z+1 because their factors in Z are all of the form 3n+2.

4. The common divisors of 72 and 96 are 1, 2, 3, 4, 6, 8, 12 and 24. All of other common divisors divide the greatest common divisor (24). We will prove in the next Module this is true in general.

5. The next largest perfect number after 6 is 28. The next two are 496 and 8128.

6. The smallest abundant number is 12. There are odd abundant numbers. If you are unable to find one now, return to this question in Module 17, Problem 7.

7. If the prime factorization of an integer n is , the divisors of n are all the integers of the form where each can take on any value from 0 to . For example, since , any divisor of 180 can be divisible by either 0, 1 or 2 powers of 2, by either 0, 1 or 2 powers of 3, and by 0 or 1 power of 5. Thus, the complete list is 1, 2, 4, 3, 6, 12, 9, 18, 36, 5, 10, 20, 15, 30, 60, 45, 90 and 180.

Module 8. Greatest Common Divisor

1. For any two integers a and b, if p₁, … p_n are all of the primes that divide either a or b (not necessarily both), then we can express a and b in the form and , where some of the values of and may be zero. Then the gcd of a and b is given by the formula . Similarly, the least common multiple of a and b is .

2. If g is the gcd of a and b, the numbers and are relatively prime because if d were a common divisor of and , dg would be a common divisor of a and b. This would contradict the fact that g is the gcd of
a and b.

3. Suppose m is the LCM of two integers a and b and M is another common multiple of a and b. If m does not divide M, then we can divide M by m to obtain a quotient q and a remainder r that is less than m. Now r = M – mq, and M and mq are both common multiples of a and b, so their difference r is also a common multiple of a and b, which contradicts that m is the least common multiple. Therefore, m½M.

4. The LCM of two relatively prime integers a and b is simply their product ab. Proof: The product clearly is a common multiple. If m is the LCM of a and b, then from the preceding problem, m½ab, so ab = mx. Since m is a multiple of a, we can write m = as and similarly m = bt. Therefore, ab = mx = asx, which implies that b = sx. Similarly, a = tx. Together, these equations show that x is a common divisor of a and b. Since (a,b) = 1, this means that x = 1 and therefore ab = m.

5. The relationship of the LCM of any two integers to their gcd is . From the preceding problem, we know that the LCM of and is the product . Clearly, if the LCM of x and y is m, then the LCM of kx and ky is km. So, setting k = (a,b), we have the LCM of a and b is .

Module 9. Euclid’s Algorithm

1. Euclid’s algorithm for a and b can be written:

a = b×q₁ + r₁

b = r₁×q₂ + r₂

r₁ = r₂×q₃ + r₃

. . . .

r_n-2 = r_n-1×q_n + r_n

r_n-1 = r_n×q_n+1.

The last equation shows that r_n divides r_n-1. Because r_n divides both terms on the right side of the second-to-last equation, that equation shows that r_n divides r_n-2. Continuing up the chain, each preceding equation allows one to conclude that r_n divides the preceding remainder, down to the third equation, which shows that r_n divides r₁. The second equation then shows that r_n divides b and the first equation then shows that r_n divides a, so that r_n is a common divisor of a and b. The proof could be made more formal, if desired by using well-ordering.

2. If d is a common divisor of a and b then from the first equation in Euclid’s algorithm, d|r₁. Since d½b and d½ r₁, the second equation shows that d½ r₂. Continuing down the chain shows that d divides each successive remainder and hence divides r_n. Again, the proof could be formalized by using
well-ordering or induction.

3. If q_n+1 = 1, then r_n-1 = r_n. But this is impermissible based on the way Euclid’s algorithm is designed. For if the last two remainders were equal, then the second-to-last equation would become r_n-2 = r_n-1×(q_n + 1) and r_n-1 would become the last non-zero remainder.

4. Euclid’s algorithm for 203 and 91 is as follows:


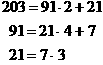
The gcd of 203 and 91 is 7.

5. Euclid’s algorithm for 144 and 89 is as follows:

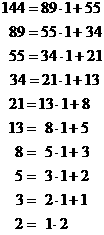
The quotients q₁ through q_n-1 are all 1, q_n = 2, and the remainders are descending Fibonacci numbers. It follows directly from the way Fibonacci numbers are defined that if a and b are successive Fibonacci numbers, the partial quotients and remainders always have these properties.

6. The gcd of 13,377 and 10,569 is 39.

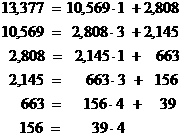
Module 10. The Diophantine Equation ax+by=1 and the
Fundamental Theorem of Arithmetic

1. If (a,b) = 1, then Multiplying both sides by c, we obtain . Since a|bc, a divides both terms on the left side of this equation and hence divides their sum, which is c. Therefore, a|c.

2. If p is prime then either p|b or Therefore, if p|bc, either p|b or, applying the previous problem, p|c.

3. This follows directly from repeated applications of the preceding problem, using induction on the number of factors if a more formal proof is desired.

4. If m has two different factorizations into primes, then any prime in one factorization would divide m and hence, by the preceding problem would divide one of the primes in the other factorization. But one prime can divide another only if the two primes are equal. Therefore, the same primes must appear in both factorizations.

5. If m has two different factorizations into primes, then from the preceding problem the same primes must appear in each factorization. If a prime p appeared with a different exponent in the two factorizations, one could divide m by the power of p with the lower of the two exponents (say pⁿ) to obtain two prime factorizations for , one of which contained p and the other of which did not. But from the preceding problem, that is impossible. Therefore, each prime must appear with the same exponent in both factorizations.