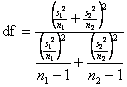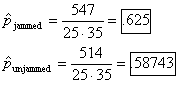|
T 3/2/010
|
HW due: Listen to this
31-minute radio program from WHYY and make at least a few written notes
on your HW paper. The interviewee, Dr. Jerry Avorn of Harvard Medical
Schools, discusses the role of statistics in health-care decisions. The
interview is several years old but is relevant to the current health care
debate in Congress. An open-notes quiz is possible.
In class: After the quiz, a general HW scan is possible. I may ask you to
produce several randomly chosen problems from randomly chosen assignments.
(First semester assignments are exempt. Only assignments from the second
semester will be subject to possible scanning.) If your assignment was copied
from another student, you will of course want to rate your score as 0 in
order to avoid a possible Honor Council case. If you cannot remember which
assignments were copied and which were your own work, you may need to rate
everything as a 0 to be safe. If, perchance, you did your own work but
functioned as the source of work for someone else to copy, you need to cross
your fingers and hope that he does the right thing and rates his assignment
as 0, since otherwise both of you could get tangled up in an Honor Council
case.
When is copying acceptable? Corrections
may be copied without causing an honor violation. When you write corrections
(in the wide right margin that you have left on your HW page, preferably
using a different color of writing), you are not asserting that the work is
yours. You are merely recording the corrections that have been gone over in
class. You are expected to have fully correct work for any problems that have
been gone over in class in detail. If you were absent on that day, you are
required to obtain the corrections from a classmate.
A placeholder (i.e., a complete statement of the givens of a problem,
possibly a sketch, and possibly some partial work, with lots of space for
adding corrections later) is acceptable for full credit, provided (1) you
have a time log documenting at least 35 minutes of focused work for that
assignment, and (2) the problem has not been covered in class. Remember, as
soon as a problem has been covered in class, the only way you can earn credit
for it is to have the corrections on your paper.
Because of the placeholder rule, it is frankly unfathomable to me why anyone
would want to copy someone else’s homework. What possible incentive is there,
given that you can earn full credit for a placeholder?
I do understand why someone would consider copying another student’s reading
notes (laziness), but I am happy to say that that particular honor violation
is exceedingly rare in my experience.
|
|
|
M 3/8/010
|
HW due: Do a “quickie” 2-sample t test (see methodology below), and redo Friday’s assignment with
an additional part (d) for #11.34 as described below. At a minimum, I expect
everyone to calculate the necessary statistics (viz., 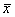 and s) for the columns of data on which
you are trying to perform tests. Based on what I saw Friday, most of you
should probably start with a fresh sheet of paper. Extensive helpful hints
are found below. and s) for the columns of data on which
you are trying to perform tests. Based on what I saw Friday, most of you
should probably start with a fresh sheet of paper. Extensive helpful hints
are found below.
Note: In our class, we will never
use the “pooled” method. Always choose “No” when asked if you want to use the
pooled method. See the middle of p. 594 for the rationale for avoiding the
pooled t test. The pooled method
was popular in the days when people had to use tables to look up their P-values, but now that we have good
computer software and graphing calculators, the pooled method is obsolete.
Just say no.
#11.34
(a) Cows are not paired with other cows. However, each treatment cow has two
readings (before and after), and those readings must be paired in order to answer the question posed in part (a).
The reason is simple: You do not have two independent SRS’s. You have one
quasi-SRS (these cows are supposed to be representative of all possible
experimental cows) that is used twice, once before treatment and once after
treatment. See the italicized passage at the bottom of p. 591 for the
justification for using this sample that is not an SRS in order to evaluate
treatment differences.
If you (erroneously) use a 2-sample t
test to answer the question posed in part (a), you will obtain a one-tailed P-value of 1.675 · 10−11,
which is essentially 0. The correct P-value,
using a 1-sample t test on the differences as your single data
column, is 1.192 · 10−11, which is also essentially 0. For
the correct test, df = 15, not 15.049.
Here is how to start the correct statistical test for part (a):
Let 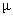 = true mean difference (“after” minus
“before”) for treated cows. = true mean difference (“after” minus
“before”) for treated cows.
H0: 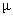 = 0 = 0
Ha: 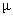 > 0 > 0
You will need to store the first column of data (16 cows) into L1,
the third column of data (same 16 cows) into L2, and the
difference (“after” minus “before”) into L3. The easiest way to do
this is with the command
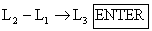
(Here, the “ ” symbol denotes the STO key, near the lower left corner of
your calculator keypad.) ” symbol denotes the STO key, near the lower left corner of
your calculator keypad.)
Then, run a 1-sample t test using
the data in L3 and the one-tailed alternative that 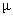 > 0. I can’t tell
you any more without giving the entire problem away, and I can’t do any more
for you without actually punching the buttons myself. Sorry! > 0. I can’t tell
you any more without giving the entire problem away, and I can’t do any more
for you without actually punching the buttons myself. Sorry!
(b) For the same reason as in part (a), it makes no sense to use a 2-sample t test here. The control cows, 14 of
them, are measured twice, and that means that we do not have independent
SRS’s.
Store the second column of data (14 cows) into L4, the fourth
column of data (same 14 cows) into L5, and the difference (“after”
minus “before”) into L6. The easiest way to do this is with the
command
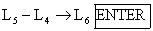
Then, run a 1-sample t test using
the data in L6 and the two-tailed alternative that 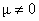 . It is interesting to note that, if anything, we see
evidence of a drop in selenium concentration in the control cows over the
9-day period. The data are not
consistent with the null hypothesis. The apparent drop could be a fluke, or
there could be something about the weather or the measuring technique that
explains the difference. The important thing to remember is that asking
questions about the control cows in isolation (or, as in part (a), asking
questions about the experimental cows in isolation) is not really part of the
research focus. What we probably want to do is to study whether the change in
selenium concentration among the experimental cows seems to be significantly
greater than the change in selenium concentration among the control cows, and
for that, we need part (d). . It is interesting to note that, if anything, we see
evidence of a drop in selenium concentration in the control cows over the
9-day period. The data are not
consistent with the null hypothesis. The apparent drop could be a fluke, or
there could be something about the weather or the measuring technique that
explains the difference. The important thing to remember is that asking
questions about the control cows in isolation (or, as in part (a), asking
questions about the experimental cows in isolation) is not really part of the
research focus. What we probably want to do is to study whether the change in
selenium concentration among the experimental cows seems to be significantly
greater than the change in selenium concentration among the control cows, and
for that, we need part (d).
(c) As discussed in class on Friday, we cannot use the paired t test for the question posed, because
the experimental and control cows are not paired. A 2-sample test is
appropriate. Use the data in L1 and L4 and a two-tailed
alternative. You should obtain a P-value
of .7088, from which we conclude that there is no evidence of a difference in
the true initial mean selenium concentrations for untreated cows and treated cows.
[Remember, that is different from saying there is evidence of no difference.
“Lack of evidence is not evidence of a lack.”]
(d) The question not posed is the one that should have been asked: Is there
evidence that treated cows’ mean selenium concentration increase is greater
than untreated cows’ mean selenium concentration increase? To answer this
question, we run a 2-sample t test
on the data in L3 and L6. Conclusion: There is
extremely strong evidence (t =
17.478, df = 15.0666, P = 1.02 · 10−11)
that the true mean selenium concentration change for treated cows exceeds
that for untreated cows. Do the PHA(S)TPC writeup for this part. (I have
already given you the conclusion.)
#11.39
Use a paired 1-sample t test. If
you do this correctly, you should obtain t
= −8.134, df = 5, P =
.000228.
Methodology for “Mini 2-Sample t Test Project”:
Recruit a volunteer family member as your test subject. Hold a ruler from the
top, with your subject’s thumb and forefinger at the bottom of the ruler.
Drop the ruler at a random moment and see how long (in inches) it takes the
subject to catch the ruler. Then repeat the test while the subject has his or
her eyes closed, and say “keh” exactly at the instant you drop the ruler.
Alternate back and forth, first with the subject’s eyes open, next with the
subject’s eyes closed, for a total of 40 trials (20 in each mode). If your
timing is bad on the eyes-closed test, ignore the results and try again. The
reason for alternating the modes is to reduce the learning effect. (If you
did all the trials with eyes open, then all the trials with eyes closed, the
skill improvement would fall disproportionately on the eyes-closed trials.)
Perform a 2-sample t test to see if
there is any evidence of a difference in true mean catch distances for the
two modes. Record your raw data, as well as a PHA(S)TPC writeup. We will
compare our results in class.
Update: I will accept 20 total trials (i.e., n1 = n2
= 10) if you cannot find a willing volunteer to help you perform 40 total
trials.
|
|
|
Th 3/11/010
|
Test (100 pts.) through all of Chapter 11. Because we did not have time Wednesday to go over a
2-prop. z test example, the test
will not require you to perform a 2-prop. z
test using PHA(S)TPC procedures. However, you should be able to handle a
2-prop. z test as a “button
pusher.” Some example problems are given below, with answers.
Problem 1: Two coins, a quarter
and a nickel, are flipped repeatedly. The quarter came from a magic store,
and there is reason to suspect that it might not be a fair coin. After 150
flips of the quarter and 150 flips of the nickel, we observe 86 heads from
the quarter and 68 heads from the nickel. Answer the following questions by
“button pushing,” i.e., without performing a full PHA(S)TPC procedure each
time. Use 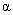 = .05. = .05.
(a) Is there evidence that the quarter is unfair?
(b) Is there evidence that the nickel is unfair?
(c) Is there evidence that the quarter’s true probability of heads differs
from that of the nickel?
(d) Explain why a paired test would not be appropriate in part (c).
Problem 2: Use 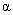 = .05 in this
problem also. Students are monitored to see if they are more likely to do
homework on nights that their cellphone signal is jammed. Jamming is
performed for each subject on random nights. Twenty-five volunteer subjects
have the following results after 35 nights of jamming and 35 nights of no
jamming: = .05 in this
problem also. Students are monitored to see if they are more likely to do
homework on nights that their cellphone signal is jammed. Jamming is
performed for each subject on random nights. Twenty-five volunteer subjects
have the following results after 35 nights of jamming and 35 nights of no
jamming:
Subj. #, count of good homework on “jammed” nights, count of good homework on
“unjammed” nights
1, 15, 23
2, 17, 15
3, 18, 17
4, 31, 32
5, 33, 30
6, 34, 31
7, 16, 17
8, 21, 19
9, 28, 22
10, 21, 21
11, 22, 18
12, 18, 12
13, 16, 15
14, 18, 17
15, 19, 16
16, 30, 28
17, 21, 23
18, 28, 24
19, 24, 26
20, 22, 24
21, 26, 21
22, 19, 18
23, 19, 14
24, 10, 12
25, 21, 19
(a) Compute the sample proportion of good homework for all jammed nights and
for all unjammed nights.
(b) Is there evidence that the true proportion of good homework increases as
a result of jamming?
(c) Explain why part (b) should not be on the AP exam. What question should
be posed instead in part (b)?
(d) Is there evidence that the mean number of good homework days increases as
a result of jamming?
Answers:
1.(a) There is no evidence (z =
1.796, P = .072) that the true
probability of heads for the quarter differs from .5.
(b) There is no evidence (z
= −1.143, P = .253) that the
true probability of heads for the nickel differs from .5.
(c) There is good evidence (z
= 2.079,  , P = .0376) that
the true probability of heads for the quarter differs from that for the
nickel. , P = .0376) that
the true probability of heads for the quarter differs from that for the
nickel.
(d) The sample flips for quarter and nickel are independent. [In
fact, there is no natural pairing that one could even contemplate here. Ask
yourself this question: If the sample sizes were not both 150, could the test
still be performed? If the answer is always yes, then pairing makes no
sense.]
Other comments for #1: We performed a two-tailed 1-prop. z test in (a) and (b), and we performed a two-tailed 2-prop. z test in (c).
2.(a)
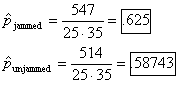
(b) A one-tailed 2-prop. z
test using the data from part (a) gives z
= 1.615, P = .053. There is no
evidence that jamming increases the true proportion of good homework. In
other words, there is no evidence that the true pjammed > punjammed.
However, a 2-prop. z test is not
really appropriate, since each subject served as his or her own control
(matched pairs). Thus we could look at the difference column (jammed −
unjammed) and see whether the additional good homework seen there (33)
constitutes a significant improvement over the .58743 proportion seen when
there was no jamming. Punching the buttons for a one-tailed 1-prop. z test with p0 = .58743, x
= 547, n = 875 gives z = 2.266, P = .0117, which is strong evidence that jamming increases the
true proportion of good homework. Do you see what happened here? Overall, the
students’ improvement as a result of jamming was not statistically
significant (P = .053), but when we
look at each student in isolation, we do see that most of them improved, and
the typical proportion improvement of .625 − .58743 = .038 = 3.8% is
statistically significant (P =
.0117) when matched pairs are used. The whole purpose of matched pairs is to
reduce the subject-to-subject variability so that the experimental effect, if
any, can be more readily detected against the background noise.
(c) The tests in part (b), strictly speaking, are invalid because
the assumptions for the z test are
not met. The trials are not an SRS
(or, in the 2-prop. case, a pair of independent SRS’s). They are actually a
stratified random sample, not an SRS, with 70 trials from each subject.
Remember, there were always 35
jammed homework nights and 35 unjammed homework nights that were used in the
experiment. Thus the sample data of 1750 homework results, while reasonably
close to an SRS, are not a true SRS since there was no possibility of, say,
selecting 25 days’ worth of data from one subject and 28 days’ worth from
another. Since an SRS has to give equal probability to all possible subsets from the universe of possibilities, we
clearly do not have an SRS. The AP would usually not cast the problem in such
a confusing light, since (strictly speaking) they would be leading you down
an invalid path. Instead, the question should be posed as follows: “Is there
evidence that the true mean number of good homework days increases as a
result of jamming?” If we did that, we would have a sample that could
reasonably be treated as an experimental SRS, following the italicized
guidance at the bottom of p. 591 of your textbook. Our real goal here is to test
treatment differences, not to generalize the effect size (“ES”) to some
larger population of interest.
(d) Pairing is appropriate, since each subject serves as his or
her own control (matched pairs). Thus we perform a one-tailed 1-sample t test (not 2-sample) and obtain t
= 2.0895, df = 24, P = .0237, which
is good evidence that jamming increases the mean number of good homework
days. The effect size (ES) has a 95% confidence interval of 1.32 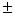 1.3038.
Interpretation in context: We are 95% confident that the true mean increase
in good homework days (out of 35) caused by jamming is somewhere between
.0162 and 2.6238. Since this C.I. avoids 0, we know that the improvement is
statistically significant. 1.3038.
Interpretation in context: We are 95% confident that the true mean increase
in good homework days (out of 35) caused by jamming is somewhere between
.0162 and 2.6238. Since this C.I. avoids 0, we know that the improvement is
statistically significant.
Other comments for #2: If you had trouble achieving the results in part (d),
please remember that you must subtract the two lists and store the result
(the column of changes) into a third list. Then perform a 1-sample t test on that column of changes,
using a one-tailed alternative against the null hypothesis that the mean is
0. If you erroneously perform a 2-sample t
test (i.e., ignoring the matched pairs design of the experiment), then you
will obtain t = .796, df = 47.856, P = .215, which would seem to suggest
no evidence that jamming improves mean homework outcomes. That is the
opposite of the conclusion we achieved in part (d). Hopefully you can see
through this example how important it is to understand when to use pairing
and when not to.
|
|
|
T 3/16/010
|
HW due: Because of a
technical glitch in posting the assignment on time, this work is not due
until Wednesday.
1. Read pp. 647-656. Since you will have to read this eventually, you might
as well get started.
2. Calculate the 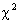 statistic and P-value for the data we gathered in
class yesterday. Remember, df = (# of bins) − 1 = 13, and the statistic and P-value for the data we gathered in
class yesterday. Remember, df = (# of bins) − 1 = 13, and the 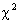 statistic itself is
the sum of scaled squared deviations from what we expected. The expected
counts are each statistic itself is
the sum of scaled squared deviations from what we expected. The expected
counts are each 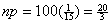 , except for “volunteer,” which has expected count , except for “volunteer,” which has expected count 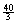 . The data we gathered were as follows: Mr. Hansen, 8;
volunteer 10; students 7, 6, 5, 6, 9, 8, 5, 8, 8, 3, 8, 9. Note: The total was 100, not 105 as we
believed during class. . The data we gathered were as follows: Mr. Hansen, 8;
volunteer 10; students 7, 6, 5, 6, 9, 8, 5, 8, 8, 3, 8, 9. Note: The total was 100, not 105 as we
believed during class.
For example, the contribution to 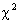 from Mr. Hansen’s
count is from Mr. Hansen’s
count is 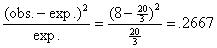 . .
[Note: This value was incorrectly
written multiple times on the whiteboard. If you were taking notes (hey, it’s
possible!), you will want to make the corrections to your notes.]
3. Write out the hypotheses and conclusion for the test of Smokey randomness.
If the total contribution from all 14 bins exceeds the critical value
(namely, 22.362), then we would have good evidence against the null
hypothesis. (Recall that the null hypothesis was that all true probabilities
were 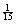 except for “volunteer,”
which was except for “volunteer,”
which was 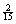 .) .)
4. Calculate the actual P-value
that supports your conclusion in #3. There are two ways to do this. Do both
of them, even if you have a more recent calculator with the built-in 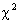 g.o.f. feature. g.o.f. feature.
(a) Execute STAT TESTS 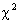 g.o.f.
(goodness-of-fit), and punch the buttons to get the answer (use a friend’s
calculator if yours is of the older type). g.o.f.
(goodness-of-fit), and punch the buttons to get the answer (use a friend’s
calculator if yours is of the older type).
(b) Download and execute the CHISQGOF program.
|
|