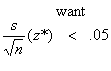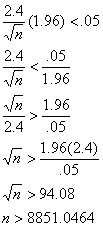|
M 2/1/010
|
HW due: Read pp. 525-529; write #9.53, 9.54, 9.57.
The third problem, which is the hardest, is set up and partially solved for
you below. You may copy my work without penalty if you wish.
9.57. We want n such that a 95%
C.I. for p has m.o.e. 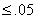 . .
We know [from Friday’s class]
that m.o.e. = (s.e.)(crit. value), and here, s.e. = 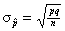 . .
Since we do not know p and q, we have to make a guess at 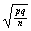 . .
Note, however, that the
numerator is maximized when p = q = .5. [Try it! There are no other
choices for p and q that produce a larger value. That is because q = 1 − p. Therefore, pq =
p(1 − p) = p − p2, and as you learned in precal, that is a quadratic
(parabola) opening down.
The vertex occurs where p = .5.]
Therefore, we know 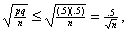 and we want this
final expression, when and we want this
final expression, when
multiplied by the critical
value, to be 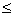 .05. The critical
value is found in the very last .05. The critical
value is found in the very last
line of the table on the
inside back cover of your textbook (labeled “z critical values”).
Solve the inequality for n, and that’s that.
|
|
|
T 2/2/010
|
HW due: Study for Wednesday’s test. I would strongly
recommend that you work several odd-numbered problems from the chapter review
exercises. There is no additional written work that will be collected,
because you were given rather short notice for the upcoming test. However, it
cannot be later in the week because of NAEP and other scheduling
difficulties.
|
|
|
|
Per your request, here is another worked example
problem of the “find the required sample size” genre:
You have been hired as a researcher to determine the mean number of mature
trees that Chevy Chase residents have on each lot. Most lots are between an
eighth of an acre and half an acre, although there are a few outliers. The
standard deviation in tree counts per lot appears to be approximately 2.4,
based on pilot testing. How large a random sample is needed to estimate, with
95% confidence, the mean tree count per lot to the nearest tenth of a tree
(i.e., with an error of less than .05)?
Solution: This problem, in order
to be done “correctly,” would require
a spreadsheet or specialized software, since you would need to use t distributions where the degrees of
freedom are adjustable. You can’t simply solve an inequality to find the
answer, since each t distribution
has a slightly different shape. You would need to use an iterative process,
which is easy on a spreadsheet, but that would go beyond the scope of our
course and beyond anything you would be asked to do on the AP exam.
However, since we know we will be using a large sample in order to get such
high accuracy, the normal curve is a reasonable approximation for the t curves that we “ought” to be using.
Check assumptions:
1. Do we have an SRS? Yes. (We will go to the office of the recorder of deeds
and will use a random number generator to choose lots from the database.)
2. Is the population normal? No! There is surely some skewness (right
skewness, most likely, if there are a few large, heavily wooded lots).
However, with a large sample (n
> 40), only extreme skewness would prevent the z curve given by 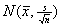 from being a
reasonable model for the sampling distribution of from being a
reasonable model for the sampling distribution of 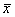 . Proceed with caution. . Proceed with caution.
Since 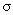 is unknown (as is always the case in
real-world situations), we will use s
as an estimate of is unknown (as is always the case in
real-world situations), we will use s
as an estimate of 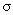 . .
Set up an inequality: m.o.e. = (s.e.)(z*)
< .05 is what we want to be true. (You can write the word “want”
over the less-than sign to make this clear.)
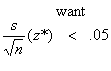
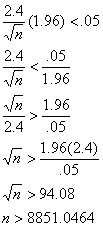
Note 1: Did you catch how the
inequality sign flips when we take reciprocals? You were supposed to have
learned that in Algebra II. There is a reason that Algebra II and Precal are
prerequisites for our class.
Note 2: We must always round up in
problems of this type.
Answer: A sample size of 8852
lots will be required. The cost of performing a tree survey on such a
large number of properties would be unaffordably high. Moreover, since 8852
is more than the number of housing units in Chevy Chase, the question is
ill-posed. There is no way to use sampling to obtain the required accuracy;
the only option is to perform a census of all trees on all lots in Chevy
Chase, which would be extremely expensive.
Modified problem: The client has decided that accuracy to the nearest tree
(i.e., error of no more than .5) will be acceptable. Does this reduce the
cost?
Solution: Indeed it does. Since
m.o.e. follows an inverse square root law (this is true in both proportion
problems and sample mean problems, by the way), enlarging the m.o.e. by a
factor of 10 allows us to reduce the sample size by a factor of 100.
Revised Answer: A sample size of 89
lots will be required. This is still considered a “large” sample, which means
that the normal approximation is reasonably accurate, even though the t distribution would be better. If you
feel worried, you might want to increase the sample size (say, to 100) to
improve the robustness of the estimate.
Also note that the quality of the estimate, as measured by the size of the
m.o.e., depends on the sample s.d. (s) that you found during the pilot
test. What if the pilot test was inaccurate? What if the real population s.d.
is more like 5 trees instead of 2.4 trees? To guard against this sort of
difficulty, you would perform what is called a sensitivity analysis on
the value of s. If s doubles, you will need to increase your
sample size by a factor of the square root of 2, which is about 1.414.
Bottom line? If your client can afford to pay for sampling 150 lots, that
would probably be a good thing. Remember, though, that research is expensive.
Performing a tree survey on 150 lots would cost thousands of dollars for the
data gathering alone, even in a region as compact and easy to survey as Chevy
Chase. You could save money by performing a satellite imagery survey (Google
Earth or equivalent), but even that would cost a fair amount of money, and
your counts might not be as accurate.
|
|
|
W 2/3/010
|
Test (100
pts.) on all material covered since the midterm exam, plus one question
(regarding LSRL and residual plots) that was fumbled by numerous people on
the midterm. Textbook passages upon
which the greatest focus will be placed are pp. 461-529.
Note: The most probable outcome for
today is that the start of school will be delayed because of snow. The
temperature will warm up quickly, and I think it is unlikely that the entire
day will be canceled. If we have a short period, I will shorten the test
appropriately. As noted above, it would be difficult to move the test to
Thursday.
If you wish to take the test from 2:15 to 3:15 in the Math Lab, I will
provide an alternate version. You must come to class at the scheduled time
for roll call, even if you wish to take the test later in the day.
|
|
|
Th 2/4/010
|
LOCATION
NOTICE: Class today will be held in SB-202, a.k.a. the freshman study hall
room, because of NAEP testing in our usual classroom.
No additional HW is due today.
|
|
|
F 2/5/010
|
Double
Quiz (20 pts.) on previously assigned
textbook reading, pp. 461-529.
No additional HW is due today.
|
|
|
M
2/8/010
|
No school because of the Snowpocalypse!
However, there will be an assignment for Tuesday, Wednesday, and Thursday, regardless of whether or not St. Albans is
in session. Be sure to check here each day by 3:00 p.m. for the following
day’s assignment. If time permits, I may post some additional video links or
other resources to help you learn the material without having the benefit of
classroom discussion. If the textbook and other materials prove inadequate,
please see my contact information and call me on
my 24-hour number.
|
|
|
T
2/9/010
|
HW due: Read pp. 531-534 and this web page; then
(in view of what you have just read), read pp. 531-534 a second time. Write
#10.1, 10.3, 10.4, 10.9, 10.12.
Note: This assignment is due Tuesday
and will be scanned when we return to school, regardless of whenever that
might be.
|
|
|
W
2/10/010
|
HW due:
Read pp. 537-548; write #10.19, 10.23.
Note: This assignment is due Wednesday
and will be scanned when we return to school, regardless of whenever that
might be.
|
|
|
Th
2/11/010
|
HW due:
Read pp. 537-548 a second time and the PHASTPC instructions; write up
Example 10.12 (pp. 546-547) using the PHASTPC format, referring to your
textbook as necessary.
Note: This assignment is due Thursday and will be scanned when we return to
school, regardless of whenever that might be.
|
|
|
F
2/12/010
|
No school (teacher work
day).
|
|
|
M
2/15/010
|
No school (holiday).
|
|
|
T 2/16/010
|
Normal school day.
|
|
|
W 2/17/010
|
No additional HW due today. The three assignments from
last week will be collected, however.
|
|
|
Th 2/18/010
|
HW due: Read pp. 550-558; write #10.39 using PHASTPC format.
|
|
|
F 2/19/010
|
No additional HW is due. However, make sure that all
your previously assigned problems are in truly wonderful shape.
|
|
|
M 2/22/010
|
HW due: Read pp. 562-567;
skip pp. 568-570; read pp. 571 (bottom)-574 (top), plus the summary on pp.
575-576. Write #10.65 (with sketches), 10.77, 10.91.
The answers to #10.65 are given in the back of the book, but if you copy them
without making sketches, you will learn nothing. Below is an example of a
problem I assigned in 2007. Look at the sketches and try to understand what
is going on.
Given: Let H0: 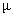 = 6 and Ha: = 6 and Ha: 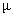 < 6 be our
hypotheses, and let s = 4.8. Let
the sample size be n = 25. We will
use < 6 be our
hypotheses, and let s = 4.8. Let
the sample size be n = 25. We will
use 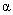 = .05 for part (a)
only. Remember, a is a “cutoff value” for P,
.i.e., the value of P below which
we will reject H0. = .05 for part (a)
only. Remember, a is a “cutoff value” for P,
.i.e., the value of P below which
we will reject H0.
(a) Draw a sketch and estimate the
power of the test against the alternative 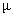 = 5.3. In other
words, how effective is the test at avoiding Type II error if the true value
of = 5.3. In other
words, how effective is the test at avoiding Type II error if the true value
of 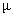 happens to be 5.3?
Your sketch should include two sampling distributions (null and alternative),
as well as a clear vertical line that separates the “reject” and “do not
reject” regions. happens to be 5.3?
Your sketch should include two sampling distributions (null and alternative),
as well as a clear vertical line that separates the “reject” and “do not
reject” regions.
(b) Draw a sketch to show how power changes if we allow a greater level of
Type I error, and if we shift the alternative hypothesis slightly upward, but
if everything else stays the same.
Solution to part (a):
Begin by sketching two sampling distributions for 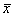 . One distribution (the “H0 distribution”) is
centered on 6, while the other distribution (the “Ha
distribution”) is centered on 5.3. . One distribution (the “H0 distribution”) is
centered on 6, while the other distribution (the “Ha
distribution”) is centered on 5.3.

To find the power, we begin by computing s.e. = 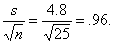
We can estimate our power by using the z
distribution. [A more exact method requires t distributions or the curves from the omitted reading on p. 568,
but both of those methods are outside the scope of the AP syllabus.]
The cutoff value for significance, shown by the bold vertical line in the
sketch, is 4.42094 [calculator keystrokes: invNorm(.05,6,.96)]. If 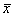 falls to the left of
that cutoff line, we will reject H0, whereas if falls to the left of
that cutoff line, we will reject H0, whereas if 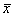 falls to the right
of that cutoff line, we will fail to reject H0. falls to the right
of that cutoff line, we will fail to reject H0.
Since power may be defined as the portion of the alternative distribution
that lies within the “reject” zone, we can estimate power to be .180
[calculator keystrokes: normalcdf(-99999,4.42094,5.3,.96)].
Even though this is only an approximation based on using z (when we should really be using t), we can “guesstimate” the power to be approx. 20%, which means
that 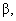 the probability of
Type II error, is approximately 80% for the 5.3 alternative. the probability of
Type II error, is approximately 80% for the 5.3 alternative.
That is low power! However, you can see that the test would be much more
powerful against a lower alternative such as 4.3, since then most of the
alternative distribution would be safely in the “reject” zone.
Remember that you cannot show calculator keystrokes on your writeup unless
they are Xed out.
Note: If you simply cannot handle
the normalcdf calculations, you can estimate power from careful sketch work
alone. The important thing is that you must make your sketch so that it
respects the horizontal axis values. In particular, s.e. must be drawn to scale.
Solution to part (b):

We know that there is usually a tradeoff between Type I and Type II error.
Specifically, we know that allowing Type I probability to increase will allow
Type II error to decrease, thus increasing power. (One exception to this
tradeoff rule is an increase in n,
which will reduce both the probability of Type I error and the probability of
Type II error.) In this problem, however, 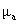 has shifted to the
right. The diagram, as drawn, shows that power (shaded) has stayed exactly
the same. We may summarize this concept by saying that if the alternative of
interest is moved closer to the null hypothesis, then power will decrease
unless we accept a higher probability of Type I error, in which case we may be
able to keep power the same. has shifted to the
right. The diagram, as drawn, shows that power (shaded) has stayed exactly
the same. We may summarize this concept by saying that if the alternative of
interest is moved closer to the null hypothesis, then power will decrease
unless we accept a higher probability of Type I error, in which case we may be
able to keep power the same.
|
|
|
T 2/23/010
|
No additional HW due.
In class: Review, catch up, and get all of your questions answered.
|
|
|
W 2/24/010
|
No additional HW due. However, now that you have had
plenty of time to think about the previously assigned problems, especially
the sketches that were due on 2/22, I expect them to be quite good.
|
|
|
Th 2/25/010
|
HW due: Execute the following problems as “button
pushers,” i.e., as if they were posed as AP multiple-choice questions where
work did not count. In other words, simply use your calculator to answer the
questions posed. In some cases you must also write a thoughtful sentence or
two.
Do these problems: #9.62, 9.64, 9.66, 10.84, 10.92.
For the first three, note that each one requires an interpretation sentence (e.g., “We are 90% confident that . . .”)
as part of your answer. For the last two, note that each one requires an
answer (yes or no) as well as a P-value
and a decision regarding H0.
This is a short homework assignment, and if you know what you are doing, you
can finish it in 10-15 minutes. However, an intelligent student who wishes to
maximize his performance on Monday’s test will also work on a selection of
odd-numbered problems each night, regardless of whether they have been
assigned or not. Why? Simply as a way to get instant feedback. The name of
the game is learning.
Note: Because there is no work
shown this time, it will be virtually impossible for me to determine whether
you have done your own work. If you copy someone’s work, you are not only
committing an honor offense (which, on this assignment, can be neither
detected nor proved) but also cheating yourself, since you are losing out on
the chance to hone and improve your skills in advance of the test.
|
|
|
F 2/26/010
|
HW due: Write #10.60, 10.62, 10.64, and the problem
below. For the first 3, you must do at least 2 of them as full PHA(S)TPC
procedures. (I recommend doing all 3 as PHA(S)TPC, but if time is short, you
may do one of them as a button-pusher without penalty.) Remember that in your
assumptions, you should identify the test you are using.
Additional problem:
By means of sketch(es) and a short paragraph of explanation, show that
constant 75% power against flexible alternatives leads to an increase in Type
I error probability for alternatives that are closer to the null-hypothesis
value of the parameter in either a one-tailed or a two-tailed test. In other
words, let power be fixed at .75, and consider an alternative that has a
certain probability of Type I error. Show that a different alternative that
also has .75 power but is centered closer to p0 (or 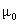 , as the case may be) will have a greater , as the case may be) will have a greater 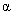 than the value of than the value of 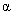 associated with the
first alternative. associated with the
first alternative.
By your request, detailed
solutions for this assignment are now available. Please see instructions
in the 3/1 calendar entry.
|
|