|
M 1/4/010
|
Classes resume.
In class: Probabilities of all hands of 5-card draw poker on the deal; review
of multiplication rule, permutations, combinations, counting rules, “at least
one” problems, binomial probabilities.
|
|
|
T 1/5/010
|
HW due: Work on your group project. By today I would
like to have your final submissions or, if that is not possible, a tight
estimate of your submission date.
|
|
|
W 1/6/010
|
HW due: Write up all of yesterday’s
CFU, and work on your group project.
|
|
|
Th 1/7/010
|
HW due: Finish up your group project, and make sure your
writeup complies with the spirit of the project
requirements from earlier this year.
In class: YIFLI dry run.
|
|
|
F 1/8/010
|
End of second quarter. All items to be graded must
be submitted. Extra credit Mathcross puzzles
must be submitted to me, in person, by 3:00 p.m.
In class: YIFLI test (YIFLI stands
for “Yes, I Finally Learned It”). Here are the rules for how this will work:
1. You must attend class, so that you can learn not only from your questions
but from everyone else’s questions as well.
2. However, participation in the oral YIFLI questions is voluntary.
3. Your YIFLI score cannot hurt you. If you do well, it can help you. I am
not announcing the weighting in advance, because some people may need an
extreme amount of help in order to pass for the second quarter.
4. Questions will be posed randomly. While the recipient of the question is
pondering his answer, everyone else should write down a response on a piece
of paper (to be provided by Mr. Hansen). When time is called, everyone will
put his pencil down, and Mr. Hansen will adjudicate the response of the
person who is in the “hot seat.” Then, everyone who has a substantially
equivalent answer may submit it to earn credit.
5. The format of the YIFLI test is such that you cannot score big simply by
getting lucky on a few questions. On the plus side, however, you will not go
down in flames if your only problem is being unable to think on your feet.
(That is because you can submit written responses to the other students’
questions.)
6. No YIFLI credit, however, will be awarded to people who decline to
participate in the oral portion.
7. Additional rules may be added at Mr. Hansen’s discretion after the game is
in progress.
|
|
|
M 1/11/010
|
Your fearless teacher made a mistake in the answer
key for problem #6(b) from the Dec. 17 test. Since the sample size is now 30,
not 2, I should of course have used n
= 30 in the formula the second time. The correct standard deviation of 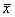 is therefore .091.
(My original answer would be “ECF” but not full credit!) is therefore .091.
(My original answer would be “ECF” but not full credit!)
I will be on campus Monday afternoon beginning at approximately 1:30, if you
have any questions or would like to see your older papers. I will also be
available for consultation via e-mail.
Thank you for a wonderful semester!
|
|
|
Th 1/14/010
|
Midterm
Exam, 11:00 a.m. − 1:00 p.m., Trapier Theater.
|
|
|
M 1/18/010
|
No school (holiday).
|
|
|
T 1/19/010
|
No school (teacher work day).
|
|
|
W 1/20/010
|
Classes resume.
|
|
|
Th 1/21/010
|
HW due: Correct your multiple-choice questions from
the exam, to 100%.
|
|
|
F 1/22/010
|
HW due (Minjae’s group plus Lyon, Graham, Nicholas):
Revise the missing parts from your final exam. Minjae’s group has one
free-response question, while Minjae, Lyon, Graham, and Nicholas all need to
revise the multiple-choice questions until they are 100% correct.
Everyone else has a night off with no homework.
In class: The sampling distribution of 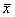 . .
|
|
|
M 1/25/010
|
HW due: Read pp. 461-466, 475-480, 482-489.
Note concerning pp. 461-466: In the
first group of pages, remember that we will use the symbol 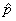 for the sample
proportion (what your book calls p).
Remember, for the sample
proportion (what your book calls p).
Remember, 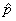 is a statistic. The
subject of pp. 461-466 is the sampling distribution of is a statistic. The
subject of pp. 461-466 is the sampling distribution of 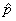 . The parameter being estimated is what we will call p. (Your book calls it . The parameter being estimated is what we will call p. (Your book calls it 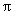 . Please make the adjustment in your head as you read.) . Please make the adjustment in your head as you read.)
To summarize:
Statistic (in book): p
Statistic (on AP exam): 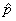
Name of statistic: sample proportion.
What your book calls p, we will
call 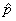 . .
Parameter (in book): 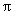
Parameter (on AP exam): p
Name of parameter: population proportion, or the true probability.
What your book calls 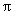 , we will call p. , we will call p.
Note concerning p. 487: Read the
italicized passages on p. 487 with extra-special care and attention.
|
|
|
T 1/26/010
|
HW due: Read pp. 490-492, 495-505.
|
|
|
W 1/27/010
|
HW due: Each group should produce a minimum of two
proposed experimental methodology statements (three are preferred). Attempt
to address the issues of control,
random assignment, and replication in your writeups. If one or more group
members are absent, the assignment must be delivered by some means in time
for the start of class, since we will be discussing and revising the
proposals.
Group 1: Nick, Eric, Ben
Group 2: Paul, Thomas, Arya
Group 3: Jeff, Minjae, Lyon
Group 4: Connor, Robbie, Graham
Control: Use blinding, double
blinding (if appropriate), placebo control, control group, blocking/matched
pairs, or various other tactics in order to control all reasonably
foreseeable lurking variables to the extent possible. The idea is that when
treatment is assigned or withheld, the assignment of treatment is the only systematic difference; all other
factors are essentially the same. Of course, this is impossible in practice,
because your experimental subjects are all different in various ways, many of
which may affect the outcome of your experiment. However, the next two
principles address this shortcoming.
Random Assignment: The decision of
whether any particular subject receives the experimental treatment or not
must be made randomly, not
according to the whim of the experimenter or any systematic assignment
procedure. (For example, it is not acceptable to tell the subjects to line up
and then count them off, “One, two, one, two, one, two,” to determine who
gets treatment and who gets no treatment, or if you have multiple levels of
treatment, to divide them into groups according to some systematic
procedure.) Assignment of treatments
must be made randomly.
Replication: You must have a large
enough sample so that the ES (effect size) that you can reasonably expect to
find cannot be plausibly explained by chance alone. For example, if I assign
quarters to one group and pennies to another group and see if the proportion
of heads differs when the subjects start flipping coins, is it meaningful to
speak of a “25 percentage point gap between the observed proportion of
heads”? Answer: Only if there were enough flips in each group to give some
statistical power to the test. (Power is defined as 1 − 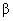 , where , where 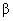 denotes the
probability of Type II error.) After all, if each group made 4 flips, and one
group had a sample proportion of heads of .5 and the other group had a sample
proportion of heads of .75, then the results are plausibly explained by
chance alone. The difference might be due to some difference between quarters
and pennies, but common sense does not allow us to rule out mere chance. The
binomial distribution tells us that a 3-1 or 4-0 split ( denotes the
probability of Type II error.) After all, if each group made 4 flips, and one
group had a sample proportion of heads of .5 and the other group had a sample
proportion of heads of .75, then the results are plausibly explained by
chance alone. The difference might be due to some difference between quarters
and pennies, but common sense does not allow us to rule out mere chance. The
binomial distribution tells us that a 3-1 or 4-0 split (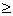 .75 heads) occurs more than 31% of the time when n = 4 even if the coin is perfectly
fair—hardly impressive evidence of a one-sided difference. .75 heads) occurs more than 31% of the time when n = 4 even if the coin is perfectly
fair—hardly impressive evidence of a one-sided difference.
For our group project, we will use 25 subjects, since for most projects that is
an adequate sample size. However, we could perform a pilot test to estimate
the ES, followed by a power analysis to make sure that n = 25 would provide adequate power. The details are messy, but I
will help you through them when the time comes.
|
|
|
Th 1/28/010
|
HW due: Rewrite one of your methodology statements,
or one of the ones that you heard from another group. Explicitly treat each of the three topics in boldface from above.
An example is furnished below.
Research question: Do English
teachers at STA have a grading bias toward themes written in “female”
handwriting?
Methodology: Twelve students, six
from STA and six from NCS, will be used as sources of handwriting. Each
student will handwrite two mediocre student themes found on the Internet, complete
with spelling errors, grammatical errors, awkward wording, and whatever was
contained in the original text. One theme will be from a teenaged male
writer, and the other will be from a teenaged female writer. There will be 12
themes in all, randomly assigned to the student participants in such a way
that
(a) each theme is written twice, once by a female scribe and once by a male
scribe, and
(b) each scribe writes two themes, one by a female author and one by a male
author.
The themes will be chosen in advance, with the assistance of an NCS English
teacher, to be comparable in quality without regard to the gender of the
writer. Themes will then be graded by each member of the STA English
department who agrees to participate in the experiment. Themes will be
randomly assigned to the graders in such a way that each grader receives all
12 themes, randomly subdivided as follows: three MM (male writer, male
scribe), three MF (male writer, female scribe), three FM (female writer, male
scribe), and three FF (female writer, female scribe).
The experimental treatments, of which there are four, are the choice of the
written source text and scribe: MM, MF, FM, and FF. Since each subject
(teacher) receives all four treatments, this is a “matched quadruple” experimental
design.
Control: All extraneous factors
are held constant or randomized. The only material differences among the
themes that the teachers receive are the treatments (MM, MF, FM, or FF).
While it is true that the graders and themes have individual differences, the
randomization (see below) will remove systematic differences.
Randomization: Random assignment
of treatments to subjects is as discussed above. Additionally, as each
package of 12 themes is being assembled for a teacher, the order within the
package shall be randomized so that there is no systematic “clumping” of
treatments. (Without this step, for example, it is conceivable that all the
FF themes appear last in the packages and are therefore graded lower, on
average, because of a lurking variable related to teacher exhaustion, having
nothing to do with the gender of the author or scribe.)
Replication: Although we have not
conducted a pilot study to see whether 12 themes is a large enough population
to detect the ES we expect to see, we feel that 12 is the largest group of
themes that our volunteer teachers would be willing to grade at no cost.
Although a probability of Type II error no doubt remains, we are confident
that the bias toward “female” handwriting is so strong that it will be evident
even with our relatively small sample size.
|
|
|
F 1/29/010
|
Class will
meet today in MH-311.
HW due: Read pp. 508-513, 517; write Activity 9.4 on p. 516.
|
|