|
T 12/1/09
|
No additional HW due. You have already endured a
test on the first day back after a break.
|
|
|
W 12/2/09
|
HW due: Read pp. 357-373.
|
|
|
Th 12/3/09
|
HW due: Read pp. 373-383; write #7.29, 7.30.
|
|
|
F 12/4/09
|
HW due: Read pp. 386-394; write #7.40, 7.41, 7.46.
|
|
|
M 12/7/09
|
Quiz (10
pts.) on the most recent Quick
Study column. Handwritten notes are permitted. Please note that there are
two short studies that you need to read.
HW due: Read pp. 397-412; write #7.56.
|
|
|
T 12/8/09
|
HW due: Read pp. 414-421; write #7.86 and correct yesterday’s
HW from the following answer key. Note that the work shown is required, not
optional.
(a) binomial with n = 100, p = .2; this is also called a B(100, .2) distribution
(b) E(X) = np = 100(.2) = 20
(c) Var(X) = npq = 100(.2)(.8) = 16
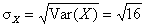 = 4 = 4
(d) A score of 50 or above is extremely unlikely, since that would be more
than 7 standard deviations above the mean. The probability (by calc.) of
scoring 50 or above by chance alone is approximately 2.1 · 10−11,
which is essentially 0. [The keystrokes binomcdf(100,.2,49) cannot be shown,
since they are calculator notation, but you should show the following work.]
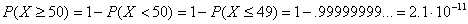
In class: Work on group projects. If a project leader is absent, he must
deputize somebody in advance. (If leaderless members show up with no
appointed deputy, there will be a small point deduction.)
|
|
|
W 12/9/09
|
HW due: Write a revised, more detailed project
proposal and adjusted timeline. I would like all projects completed by Dec.
18 if possible, so that you will have less hanging over your head during the
break. Exceptions will be permitted, but Dec. 18 is a good target date. If
your group leader is absent, he must deputize somebody to deliver the
product. Neatness and grammar count.
|
|
|
Th 12/10/09
|
HW due: Turn in your revised group proposals at
start of class; read pp. 445-449 (note:
we are skipping pp. 425-428); write #7.60, 7.106ab, 7.110, and the following
additional questions:
(a) Why did we study random variables before proceeding to Chapter 8? Or,
more to the point, why did we study random variables at all?
(b) When we write B(n, p),
we mean a binomial distribution with parameters n and p. For example,
the count of sixes when we roll a fair die 77 times follows the B(77, 0.1667) distribution. Similarly,
we write 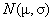 to refer to a normal
distribution with mean to refer to a normal
distribution with mean 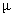 and standard
deviation and standard
deviation 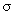 . Suppose that STA Upper School students’ heights follow
the N(71, 3) distribution and that
NCS Upper School students’ heights follow the N(66, 2.5) distribution, where all measurements are in inches. An
Upper School prom couple is formed by selecting an STA boy and pairing him
with an NCS girl, completely at random. Compute the probability that the boy
is taller than the girl. Hint:
Consider the random variable X = S − N, where S and N denote the heights of a randomly
selected student from STA and NCS, respectively. . Suppose that STA Upper School students’ heights follow
the N(71, 3) distribution and that
NCS Upper School students’ heights follow the N(66, 2.5) distribution, where all measurements are in inches. An
Upper School prom couple is formed by selecting an STA boy and pairing him
with an NCS girl, completely at random. Compute the probability that the boy
is taller than the girl. Hint:
Consider the random variable X = S − N, where S and N denote the heights of a randomly
selected student from STA and NCS, respectively.
|
|
|
F 12/11/09
|
No additional HW due. (Work on your group projects.)
However, your HW that was due yesterday also needs to be redone in all cases.
Problem (b), especially, needs to be completed since this is a standard
AP-type problem. After you determine the mean (easy) and standard deviation
(moderately challenging) for random variable X, the problem is just like others that you have seen.
|
|
|
M 12/14/09
|
HW due: Work on your group projects, and please
finish up your previously assigned problems. Last Friday’s HW scan is not
something we want to repeat.
|
|
|
T 12/15/09
|
HW due: Patch your old HW (since it may be collected
again), read pp. 450-459, and write #8.2, 8.10, and question (c) below.
(c) In the tan box on p. 455, which statement(s) would make N. N. Taleb
(author of The Black Swan)
apoplectic, and why?
|
|
|
W 12/16/09
|
HW due: Write #8.20 (check answers below), visit the
sampling
distribution simulation (requires Java), perform the additional exercises
below, and answer the questions posed.
Answers to #8.20 (note: work is required for credit):
(a) Done in class on 12/15.
(b) The sampling distribution is approximately N(22.0, 1.65) as shown on the board in class on 12/15.
(c) 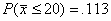 , and , and 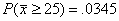 (sketches required
for full credit; remember that you are not allowed to show the normalcdf
keystrokes as part of your work) (sketches required
for full credit; remember that you are not allowed to show the normalcdf
keystrokes as part of your work)
Sampling distribution simulation exercises:
1. Click the “Begin” button to load the applet window. On your homework
paper, simply put a check mark next to the number 1 to indicate that you have
performed this step.
2. In the first dropdown box in the applet window, choose “Custom.” Use your
mouse to paint a custom distribution (anything you like, so long as it is
non-normal and irregular in shape), and sketch a relative frequency histogram
of your distribution to make a permanent record of it.
3. In the third drop-down box from the bottom, choose “N=2” so that 2 values
will be chosen to be included in each sample mean. (Note: There are some
typographical errors on this applet page. Identify them for a small bonus
credit.)
4. Using the distribution in #2 as your underlying data distribution, click
the “Animated” button. How many values are chosen to make the sample mean
that falls into the blue histogram?
5. Click the “Animated” button a few dozen times, until you become bored.
6. Now click the “5” button. This is less boring, because you can generate 5
sample means at a time.
7. Repeat step #6 until your Reps count (see at left side of window) is at
least 500. Sketch the blue histogram on your homework paper.
8. Is the sketch in #7 more irregular, less irregular, or about the same as
the histogram you sketched in #2? Write a sentence explaining why this
behavior occurs.
9. Click the “1,000” button until the Reps count is at least 40,000. Is the
blue histogram looking normal yet? Why or why not?
10. Record the standard deviation of 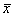 (found to the left
of the blue histogram). Is this larger or smaller than the s.d. of the
original underlying distribution? (found to the left
of the blue histogram). Is this larger or smaller than the s.d. of the
original underlying distribution?
11. Compare the means: The mean of the distribution at the top of the page is
the population mean, denoted ____ (fill in the blank), and it equals
______________ . The mean of the sampling distribution (blue histogram) is
denoted 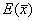 or _________ and equals ______________ . or _________ and equals ______________ .
11. In the third drop-down box from the bottom, choose “N=25” instead of
“N=2.” The blue histogram should disappear.
12. Click the “5” button a few times, until you become bored. Are the means
more or less spread out than they were before?
13. Click the “1,000” or “10,000” button until the Reps count is at least
40,000. Is the blue histogram looking normal yet? Why or why not?
14. Record the standard deviation of 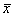 (found to the left
of the blue histogram). Is this larger or smaller than the s.d. of the
original underlying distribution? (found to the left
of the blue histogram). Is this larger or smaller than the s.d. of the
original underlying distribution?
15. According to the CLT, what should be the s.d. of 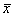 in the blue
histogram? (Show your work.) Does the CLT seem to be telling the truth here? in the blue
histogram? (Show your work.) Does the CLT seem to be telling the truth here?
16. Compare the means: The mean of the distribution at the top of the page is
the population mean, denoted ____ (fill in the blank), and it equals
______________ . The mean of the sampling distribution (blue histogram) is
denoted 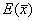 or _________ and equals ______________ . or _________ and equals ______________ .
17. The CLT includes the phrase “as n
increases without bound” or “as n
approaches infinity.” Approximately how large does n need to be before the CLT kicks in and starts to make the
sampling distribution look normal?
|
|
|
Th 12/17/09
|
Test (100
pts.) on all recent material, through p. 459 in textbook.
Important announcement: The test
will be held in MH-311 in order to provide better test seating.
Answers to #7.110 are posted below to help you study. Please note: Many,
many, many worked examples are already in your textbook, complete with
solutions and explanations. I recommend that you read through those if you
have not already done so, and maybe test to see if you can get the answers
without peeking at the solutions provided.
#7.110(a) P(player operates for at
least 4 hr) = 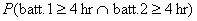
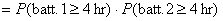 [valid only since
the batteries are independent!] [valid only since
the batteries are independent!]
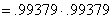 [by calc., using the
normalcdf function that you can sketch but cannot write] [by calc., using the
normalcdf function that you can sketch but cannot write]
= .988.
(b) P(player operates for at most 7 hr) = 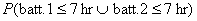
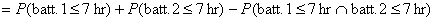
[must
use General Union Rule since the batteries could both fail on or before 7 hr]
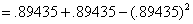 [by calc.] [by calc.]
= .989.
(b) Alternate method: P(player operates for at most 7 hr) =
1 − P(both batteries last
more than 7 hr
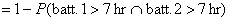
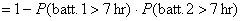 [valid only since
the batteries are independent!] [valid only since
the batteries are independent!]
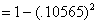 [by calc.] [by calc.]
= .989.
(c) To find z* such that 95% of cassette players
will die on or before z* hours,
consider generalizing
the
alternate method for part (b). Let a
= P(batt.1 lasts more than z* hours), so that our goal is
to
get 1 − a2 to be
exactly .95. Clearly, (b) shows us that z*
< 7, since almost 99% of cassette
players
will conk out before 7 hours. Also, z*
> 6, since a = .5 (by properties
of the normal curve)
when
we are looking at life beyond 6 hours, and 1 − a2 = 1 − (.5)2 = .75, which is
smaller than our
target.
By trial and error, we can eventually find that z* is about halfway between 6
and 7, namely
6.608
hr.
If
you are a calculator whiz, you can make a function
Y1=1−normalcdf(X,999999,6,.8)^2
and
see where that function crosses the line
Y2=.95
The
solution, using the 2nd CALC intersect function on your calculator, is
X=6.608.
If a
problem like this appears on the test, I would be happy if you could simply
show that z* is
greater
than 6 and less than 7.
|
|
|
F 12/18/09
|
Target date for submission of simulation project
writeups.
HW due: Attend Lessons & Carols at the Cathedral (7 p.m.) and make sure I
record your presence. I will be sitting near the front of the nave.
|
|
|
|
Christmas break.
|
|