|
Th 11/5/09
|
Quiz (10 pts.) on Tuesday’s Quick Study from The Washington Post. The quiz will be open-notes,
but your notes must be handwritten and must be of a summary nature. (No
printouts or transcripts are allowed.) If your parents do not get the Post, please visit the STA library or this
link.
Since we did not have class yesterday, two essays are due today:
1. (20 pts.) Write a detailed set of comments and suggestions for the packet
I distributed at lunch Tuesday. Nick still needs to pick this up from me. Do
not worry about “sugar-coating” your critique (although please note,
tactfulness is extremely important
in the real world). Legibility, spelling, and grammar all count, except that
complete sentences are not required. In other words, bulletized lists and
sentence fragments are acceptable. If you are unable to write legibly, please
type your suggestions and use numbering or some other suitable scheme to
refer to markups in the packet. You may share some ideas with classmates, but
each student’s writeup must be uniquely his own. Try to find as many good-quality suggestions for
improvement as you can. If the suggested improvement involves a trade-off
(e.g., increasing the length), please write that—so I know that you know
there is a downside as well.
2. (10 pts.) In the Wikipedia article on types of scales,
carefully read the section entitled Ordinal
scale. Also read this
USA Today article and any other related articles in print or online that
you deem appropriate. Then, write a short opinion essay (approximately 2-3
paragraphs, supported by factual arguments) attacking or defending (your
choice) the following method that most American teachers use for computing
course grades:
- Each assignment or graded item has either a
point score or a letter grade (or both) associated with it.
- There may or may not be a subdivision by
categories (e.g., tests, quizzes, HW, and class participation each
counting for a certain percentage of the overall grade). Many teachers
use these subdivisions, although Mr. Hansen does not.
- At the end of the quarter, the quarter average
is computed as the ratio of points earned to points possible. Students
whose average is 94% or above (90% at some schools) earn an A, those
whose average is 85% or above (80% at some schools) earn a B, and so on.
If the teacher does not use points, then grades are averaged by
converting letters into points and averaging; for example, two C+’s, a
D+, two A’s, and a B+, where the D+ is a test weighted at double
strength, would average out to a B- (B minus). The key is this:
Regardless of whether letter grades or points (0-100) are used, the
course grade is computed by averaging.
Recording points (or letter
grades) for each assignment, adding up the points (or letter grades) earned,
and dividing by a suitable denominator in order to compute the overall course
average grade is what is at issue here. The specific boundaries between
letter grades are not to be
discussed in your essay, nor are questions related to how heavily certain
assignments should be weighted, nor are questions concerning categories of
assignments. Essays dwelling on any of these areas will be deemed
nonresponsive and will be returned ungraded. For example, do not write about
how you think tests should be a lower percentage and daily quizzes should be
a higher percentage, or how homework should not count at all, or how class
participation grades are too subjective, or anything of a similar nature.
The question before you is
a narrow statistical question: Does
it make sense to record points for each assignment, add up the points earned,
and divide by the number of points possible? Please note, this is equivalent
(except for minor rounding issues) to recording letter grades, adding up the
letter grades, and dividing by the number of grades to find an average grade.
The question is simply this: Does averaging
grades make sense?
If you say yes, you should offer good arguments in support of your answer. If
you say no, you should not only offer good arguments but also propose an
alternative approach that makes more sense and could realistically supplant
the system that is currently used by most teachers, including Mr. Hansen, at
most schools in America. If you offer a weasel-like answer (“It depends . .
.”), you need to indicate the specific circumstances under which grade
averaging makes sense and the specific circumstances under which it does not
make sense.
There is no right or wrong answer, and this is not an easy question. (If you
wanted to, you could probably make a Ph.D. dissertation out of it.) Your
score for this assignment will be based on the originality and quality
of your arguments. As always, spelling, grammar, and punctuation also count.
|
|
|
W 11/18/09
|
HW due: Read the paragraph on p. 290 beginning with
the words “Limitations of the Classical Approach to Probability.” (Classical in this context means a priori.) Then, read the paragraph on
p. 291 entitled “Relative Frequency Approach to Probability,” the paragraph
at the bottom of p. 294 entitled “Subjective Approach to Probability,” and
the numbered summary in the middle of p. 295. If, after reading all four
passages, you believe that Tuesday’s quiz was unreasonable, you may write a
short essay clarifying your position. This essay is optional, but the reading
is required.
For your in-class work, you should meet with your group members, decide upon
a probability simulation project, and begin writing your methodology
statement and proposed timeline. Numerous project ideas are listed here. Group assignments are as follows, with
the leader underlined:
Minjae, Robbie, Graham
Arya, Eric, Jeffrey
Ben, Thomas, Nicholas
Lyon, Connor, Paul
|
|
|
M 11/30/09
|
HW due: Rework your CFU from last
Tuesday, solving each problem completely. If you have a good solution to
one or more problems (or a solution you think is pretty good), e-mail it to
me. I will post the best ones here on the website. Before you take your test,
you will need to show me that you finished your CFU. Everyone (even Eric)
should re-do all the problems for practice. It is definitely to your
advantage to do this work, since the test will be quite similar to the CFU.
Don’t wait until Sunday to start. Work a little on Friday, a little on
Saturday, and you will be in good shape for the test.
In class: Test (100 pts.) through p.
343. Eric may take this test if he wishes.
Update: As of 11:00 a.m. on Sunday,
11/29, nobody had sent me anything, except for one anonymous request to post
answers. That is not how it is supposed to work. However, here are the
answers with some of the supporting details.
1. If you can’t do the scatterplot with LSRL overlaid, you will surely fail
the test. If you code the years as x
= 9, 18, 23, and 30, i.e., as years since 1970, then the equation is 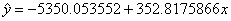 ,
where ,
where 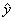 denotes predicted megabytes per dollar.
Note: You must define your variables and state how your years are coded. denotes predicted megabytes per dollar.
Note: You must define your variables and state how your years are coded.
2. Redefine your scatterplot so that the X list remains L1, but
the Y list is RESID. Hit the Y= key and turn off the display of your Y1
line (just to the right of the Y1 prompt, highlight the equal sign
and press ENTER to toggle). Then press ZOOM 9 and transcribe your plot, with x and y values, onto your paper. The bowl-shaped pattern is a big
problem, indicating that some sort of curved fit would be much more
appropriate. By pressing TRACE and using your left and right arrows to step
through the points on the residual plot, you can also see that the residuals
are all between 1000 and 3000 in absolute value. These are gigantic
residuals! Clearly, the LSRL is a poor fit to the data despite the strong
correlation coefficient (r =
.8877).
3.(a) 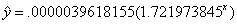 ,
where x and y are as before ,
where x and y are as before
(b) 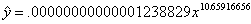 ,
where x and y are as before ,
where x and y are as before
4. You must sketch residual plots
and compare them. You should mention the r
values, but you get almost no credit if you stop there. Now, it happens to be
true that the exponential plot gives an r
value of .995, which is the strongest of the three, but the AP graders do not
accept that as adequate justification. The reduced patterning of the residual
plots for exponential and power fits are the key, and the fact that the
maximum residual size is much smaller for exponential (<3650) than for
power (almost 8900) seals the deal. Note that the r value of .995 is actually the linear correlation coefficient that you get if you make a LSRL
with x as the explanatory variable
and log y, not y, as the response variable.
Although it was not requested on the CFU, forming the LSRL fit between x and log y is highly educational. Also, it ties in nicely with what Mr.
Morris taught us last week about Moore’s Law. Make a scatterplot of x on the horizontal axis and log y on the vertical axis, and you will
see an almost perfect straight-line relationship. This straight-line
relationship between x and the log
of y is the hallmark of exponential
growth or decay! (The hallmark of a power relationship is a straight-line
relationship between log x and log y. For the data set given, there is a
fairly good fit between log x and
log y, but the fit between x and log y is stronger, as Moore’s Law would lead us to expect.)
5. No, since both could occur; yes, since neither event alters the probability
of the other; .011834.
6.
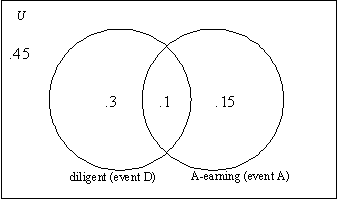
Check your work: P(D)
= .3 + .1 = .4 as required. P(A) = .1 + .15 = .25 as required.
Finally, 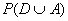 = .3 + .1 + .15 = .55 as required. The
diagram is valid! = .3 + .1 + .15 = .55 as required. The
diagram is valid!
Note that 45% of the students must float elsewhere in
the universe to make 100%.
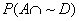 = .15 by
diagram = .15 by
diagram
P(A | D) = .1/.4 = .25 by diagram (look for the “A” students within
region “D”)
P(D | ~A) = .3/.75 = .4
P(D) = .4 (given!)
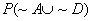 = = 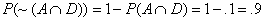
A and
D are independent since P(A
| D) = .1/.4 = .25, and P(A)
= .25 (given).
Since knowing that D has occurred does not change the probability of A, the
events are independent.
Alternate proof: Independence occurs if and
only if probabilities can be multiplied
in an intersection. We have 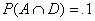 by diagram. Since by diagram. Since 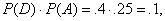
the proof is complete. Note: It is not true in general that probabilities can be
multiplied
in an intersection! This occurs only in the
case of independent events.
A and
D are not mutually exclusive, since
the probability of their joint occurrence,
namely .1, is nonzero.
7.(a) 18/36 or .5 [a table of dice rolling is required for credit]
(b) There are 27 rolls that satisfy the condition of at
least one even die. (In fact, the only rolls that fail to satisfy the
condition are (1,1), (1,3), (1,5), (3,1), (3,3), (3,5), (5,1), (5,3), and
(5.5).) Of those 27, only 9 have an even sum. The probability has decreased.
8. P(8) = P(rolling (2,6), (3,5), (4,4), (5,3), or (6,2)) = 5/36 = .13889.
The student is offering odds of 6:1 against the event of rolling an 8, but
the fair odds would be 31:5. Since 31:5 is more than 6:1, the student is understating the fair odds in an
attempt to earn a profit. The game is not fair. If the teacher were to accept
the bet, the student would win money in the long run. From the teacher’s
point of view, the expected value of the game is found by weighing a loss of
$1 (which happens most of the time) against a profit of $6 (which happens
only 5/36 of the time). Expected value = 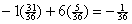 dollars, or about −$.02778. The
negative sign is required. dollars, or about −$.02778. The
negative sign is required.
9. Select pairs of random digits from a table. Ignore any digit pairs greater
than or equal to 20, as well as any digit pairs that have already been chosen
in the current iteration. (Such a pair should be ignored and replaced by the
next valid pair.) An iteration consists of a valid digit pair to indicate
“my” number, something between 00 and 19 inclusive, plus 5 more valid digit
pairs to simulate the numbers of the people closest to me at the party. If
the sum of those 5, divided by 5, is less than “my” number, record “SUCCEED”;
otherwise, record “FAIL.” The probability estimate at the end of many
iterations, say 100 iterations, equals the count of SUCCEED divided by the
total number of iterations.
10. P(at least one in top 5) = 1 −
P(none in top 5) = 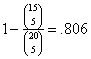
11.(a) SRS means sampling without replacement, which means that the
probabilities change as people are removed from the pool. Independence
requires sampling with replacement.
[Note: In a large population, the difference between SRS and sampling with
replacement is negligible. However, in a small population, the difference is
great.]
(b) No, since as we discussed in class, p (and, by extension, q) must be constants for the problem
in question. The probability of success in selecting a person to be among the
“top 5” is not constant as the pool diminishes in size.
12. The easiest way is to imagine 100,000 dogs. Draw a tree diagram, and
always make the first split based on the presence or absence of the disease
or trait in question (here, superslobberiness). We have 1500 affected dogs
and 98,500 unaffected.
Make the second split based on the outcomes of the test. Of the 1500 affected
by superslobberiness, the test will tag 1470 as true positives and 30 as
false negatives. Of the 98,500 unaffected, the test will tag 96,037.5 of them
as true negatives and 2462.5 as false positives. PPV = P(true pos. | pos.) = 1470/3932.5 = .374.
|
|