|
Th 10/1/09
|
HW due: Read pp. 97-113. (Reading notes are
required, as always.)
|
|
|
F 10/2/09
|
HW due: Show your steps in developing a list of 12
acquaintances sorted in random order. Use the techniques illustrated in class
yesterday.
|
|
|
M 10/5/09
|
HW due: If you have not already made your assignment from
last Friday “clean” (i.e., suitable as instructions for someone with basic
literacy but no specific technical skills with the TI-83 or TI-84
calculator), then please do so. Every middle manager needs to develop the
skill of giving clear directions to subordinates. These writeups will
probably be collected and graded. Be sure to indicate exactly what number has
been assigned to each acquaintance and what the results of the randomization
are.
HW due from each group leader: A
group proposal similar to the one due on Tuesday 9/29, except with more
detail in the methodology. Try to adjust your timeline so that you can turn
in your final report by Friday, 10/16. If your project is especially
meritorious and needs a little more time, then say so and we can probably
work with that. You will have approximately 5 minutes of class time per day
for administrative meetings with your group members, but essentially all of
the data gathering and other work will need to be performed outside of class.
Please remember that if you are using Mr. Hansen as a resource, you should
allow adequate time for responses to data requests or critiques of drafts.
Format: Group Leader Name (underlined) in upper right corner, with
other group member names and due date underneath.
If the group leader is absent today, he must deputize someone else to turn in
the proposal. If all three group members are absent, then e-mail (timestamped
by 9:50 a.m.) will be accepted, but otherwise I would strongly prefer a hard
copy. Hard copies are much easier to review and mark up for educational
purposes.
You will continue to have daily reading and writing assignments during the
next two weeks, but the length will be reduced in order to provide some time
for the group project.
Group 1: Graham, Lyon, Arya
Group 2: Thomas, MinJae, Connor
Group 3: Eric, Paul, Ben
Group 4: Robbie, Nick, Jeffrey
|
|
|
T 10/6/09
|
HW due: As announced during cleass, each group
leader will receive an e-mail on Monday evening with a critique of the group
proposal and suggestions for improvement. Please implement these (those that
you agree with, at any rate) and bring the revised version to class.
|
|
|
W 10/7/09
|
HW due (optional): Prepare a list of test-related
questions for your fearless teacher.
All groups may now begin working on projects. All proposals are approved, even
though a few typos slipped through. For example, I marked “Word Template” as
“Word template” (the “t” should be lower case) for Group 2, then forgot to
include that comment in Monday’s critique e-mail. Thomas, please implement
the capitalization change when you get a chance; there is no need to reprint
the document.
For all group leaders, please note the more significant comments below. There
is no need to print new versions of your proposals. However, please implement
these changes before you incorporate your research question and condensed
methodology into your final report.
Group 1: St. Albans does not use an apostrophe.
Group 2: Strictly speaking, your research question should use the word
“association” instead of “correlation.”
Group 3: Same comment as for group 2. Also, in your project report,
please make paragraphs much shorter.
Group 4: Same comment as for group 2. Also, I should have asked you
previously to delete the word “significant” from the research question, since
we have no way of assessing statistical significance at present.
|
|
|
Th 10/8/09
|
Test (100
pts.) on textbook through p. 113 and all material covered since the beginning
of the year. Recent material will
be emphasized, but you are still responsible for older material, such as the
definitions and symbols for sample standard deviation (s), sample mean (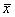 ), interquartile range (Q3 − Q1
= IQR), sample size (n), population
size (N), etc.; the definitions of
left and right skewness, explanatory and response variables, categorical and
quantitative variables, Likert scale, time series, response bias, selection
bias, robustness, sensitivity analysis, and many other terms; the procedure
for computing and plotting the least-squares regression line (LSRL) ), interquartile range (Q3 − Q1
= IQR), sample size (n), population
size (N), etc.; the definitions of
left and right skewness, explanatory and response variables, categorical and
quantitative variables, Likert scale, time series, response bias, selection
bias, robustness, sensitivity analysis, and many other terms; the procedure
for computing and plotting the least-squares regression line (LSRL) 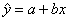 and its linear
correlation coefficient (r); and
many other topics. and its linear
correlation coefficient (r); and
many other topics.
Remember that at on nearly every test I give, at least one question will be
“from out in left field,” i.e., not based on any specific discussion that has
ever occurred in class. I do not apologize for this, since it is part of what
I have to do to help prepare you for college and the real world. There may
not be a definitive “right or wrong” answer, and you will need to use your
creativity and knowledge to address the question in some logical, thoughtful
manner.
Handwriting counts, especially in equations, where each symbol must be
unambiguous. (Remember the “quite sizzly” rules.) In paragraphs or bulletized
lists, handwriting is less critical, but I will not score any response that
requires excessive effort on my part to decipher.
|
|
|
F 10/9/09
|
HW due: Read to the end of chapter 3 (middle of p.
136); write yesterday’s test to perfection.
It is permitted to work with classmates and argue with them, as long as you
do not copy their work.
|
|
|
M 10/12/09
|
Columbus Day (no school).
|
|
|
T 10/13/09
|
HW due: Work on your group projects, and read pp.
147-156. Important: Please read the
footnote on the bottom of p. 156! Throughout the course, I will use p and q for population proportions of success and failure,
respectively, and 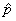 and and 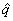 for sample
proportions of success and failure. I do this, even though the “statistic p
as an estimate of parameter for sample
proportions of success and failure. I do this, even though the “statistic p
as an estimate of parameter 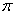 ” rule is more logically consistent with the idea of using
Roman letters for statistics and Greek letters for parameters. ” rule is more logically consistent with the idea of using
Roman letters for statistics and Greek letters for parameters.
|
|
|
W 10/14/09
|
HW due: Read pp. 159-166 carefully (more carefully
than usual); write #4.16, 4.24.
|
|
|
Th 10/15/09
|
HW due: Read pp. 169-183; make sure all previously
assigned problems are written up.
Important: During the day today
(Thursday), ask your teachers if you may attend tomorrow’s field trip to the Solar Decathlon exhibit on the
Mall.
|
|
|
F 10/16/09
|
HW due: Get plenty of sleep, and fill in your
missing gaps (e.g., #4.24) if possible.
Field Trip to the Mall (updated
schedule): Leave on bus next to Martin Gym at 10:10 a.m. sharp (15
minutes before end of B period). We will take whoever is on the bus at 10:10.
We will be gone during all of C period and will return to STA at the start of
D period. Your teachers have been asked to excuse you from C period and part
of B period if it is possible for you to miss class without disruption.
|
|
|
M 10/19/09
|
HW due: Work on your group projects.
|
|
|
T 10/20/09
|
HW due: Write the following exercises.
1. Write the definition of z score.
2. Compute the z score for a
normally distributed test on which the mean is 79, the s.d. is 8, and a
student earns an 83.
3. Compute the percentage of students that score (a) better than the student
in #2, (b) between the student in #2 and 50%.
Note: In #3, do part (a) twice,
using both the “easy” method and the “hard” method. Then do part (b) twice,
using both the “easy” method and the “hard” method.
4. Which method do you prefer in #3?
|
|
|
W 10/21/09
|
HW due: Make sure that you obtained 30.9% for #3a
and 69.1% for #3b yesterday. You must show your work properly; a sketch is required,
and the word normalcdf must be
crossed out if you use it, since it is calculator notation. Then read pp.
186-192 (reading notes required, as always). Pay special attention to the
summary on pp. 191-192.
|
|
|
Th 10/22/09
|
The test originally scheduled for today has been
postponed a day, by mutual agreement.
|
|
|
Online
Q&A
|
Q. I assume we only use the normalcdf
function when the data set has a normal distribution?
A. Correct. However, please be aware that a z score can be computed for any distribution.
The interpretation of z is always
the same: a dimensionless number that tells the number of standard deviations
(negative meaning to the left, positive meaning to the right) that a score
is, relative to the mean.
Q. If one was given a list of scores...How
could he or she find the score that represents let’s say the 68th percentile?
What about the 90th percentile?
A. If there are 101 scores in your
population, this is no problem; arrange the scores from lowest to highest and
pick the 69th (or 91st) score. Note that the lowest score is at the 0th
percentile, which is why you have to add 1 for the ranks; for example, the
101st score in the list is the 100th percentile. For populations that are not
exactly of size 101, you can interpolate or use software to do the job for
you. Excel has a function called PERCENTILE that will give you the kth percentile of any column of data
(up to 8,191 cells, that is). For example, if you wanted to find the 25th
percentile of the data in cells A15 through A35, the syntax you would use is
=PERCENTILE($a$15..$a$35,.25). Note that the percentile must be entered as a
decimal value between 0 and 1, not as an integer.
Q. What is an acceptable definition for bias?
(How about, “Bias is any factor that systematically skews data?”)
A. The definition I like is, “Any systematic
movement of a statistic away from the true parameter value.” The reason I
don’t like student definitions that include the word “skew” is that sometimes
the data you see should be skewed
(if they came from a skew right distribution, for example!). I mean, I think
I know what students mean when they say “any factor that systematically skews
the data,” but I am trying to prep you for the mean, cruel world of the AP
exam. The two key ideas to remember are (a) that bias is something systematic
(meaning tending to one side or the other, not both), and (b) that bias
affects a statistic. In order to
claim that bias exists, you must establish that the statistic is being
systematically pulled either to the high side or to the low side (but not
both ways) in relation to the true parameter value. Otherwise, your claim of
bias is as empty as that of a freshman who says, “Oh, that test was so biased
. . . the questions were taken from all parts of the reading assignment.”
Maybe the test was hard, maybe the test was painful, but biased? Sorry, only
if there is evidence that the test is systematically producing scores for
which some statistic of interest (usually the mean) has been shifted away
from what the true parameter value is, and in some consistent direction. Note
that problems with data gathering, including measurement error, sampling
error, rounding error, and even nonresponse, do not constitute bias unless
there is a systematic effect on the statistic of interest. Thus a teacher who
gives hard tests but scales everything appropriately is not guilty of bias at
all.
Yes, nonresponse is frequently a cause of bias. There is even a name for it,
nonresponse bias, since in many survey situations the people who fail to respond
are fundamentally different from those who do: the nonresponders are less
interested than the responders. If lack of interest correlates in some way
with the true proportions of people who hold various opinions being measured
(as is often the case), then bias in the survey statistics is inevitable.
But what if nonresponse were an artifact of a random process? For example,
what if all the responses were on identical paper ballots that were well
mixed, and then half of the ballots were randomly selected to be burned
without being counted at all. Does this introduce nonresponse error?
Definitely. Would this trigger a lawsuit? Almost certainly, if these were
ballots for an election. But is this a case of nonresponse bias, or even of
bias at all? No.
If you ask one head of a household in Washington, D.C., randomly selected
from a list of all households, how many people live in his or her household,
will you get an accurate estimate of mean household size? Probably not, since
your sample size is ridiculously small. But is your process biased? No.
If you ask the same question of 5,000 people in Washington, D.C., randomly
chosen from a list of residents compiled by market research firms (which have
fairly good lists), will you get an accurate estimate of mean household size?
Definitely not, but this time the problem is not that the sample size is too
small or even that the lists are inaccurate. The problem is that there is selection bias. The sampling frame is
wrong; households are no longer equally likely to be chosen, since people
from larger households count many more times in the selection pool than
people from smaller households. Thus the statistic of mean household size
will be strongly biased toward the high side.
|
|
|
F 10/23/09
|
Test #3 (100 pts.), cumulative over Chapters
1-4 and all material covered since the beginning of the year. In order to help you prepare for the test, I am
furnishing both a practice test
and an answer key. (For best
results, do not consult the answer key until after you have taken the test,
under time pressure.) In addition, any questions that you send by e-mail will
be posted above, with answers for all to see.
Because of time pressure during the test (caused either by Mr. Hansen’s
absentmindedness at forgetting to pick up the printouts or by the student
whose dress code issues created a distraction), you may expand upon your test questions via e-mail. Please send me your
enlarged responses with the following standard subject line starting with two
underscore characters (substitute your name in the subject line):
__Test 3 continuation from student
Johnson, James
Please number your responses for clarity. Also, at the very beginning of your
message, include an honor statement similar to the following:
Dear Mr. Hansen,
I certify that I worked on this e-mail message from
3:45 to 4:00 p.m. on Friday and did not use any printed, handwritten, or
electronic aids, nor did I confer with anyone else about the test before
transmitting this message.
(If you did
confer with anyone, briefly list the person and the nature of the
conversation.)
|
|
|
M 10/26/09
|
HW due: Read pp. 199-207, especially p. 207, which
is super-important.
Also, if you have not already turned in your group project, work on that. If
you have not already finished up your test, work on preparing your e-mail as
described in the 10/23 calendar entry.
Additional HW: If you were not on
campus to take Friday’s test, you should do
the entire test, with a 45-minute time limit, as a homework assignment. Bring
it to class with you.
|
|
|
T 10/27/09
|
Essay
Quest (50 pts.) covering material
since the beginning of the year. Level of difficulty will be comparable to
the example given in class yesterday. There is really no way to study or prepare
for this quiz. Please, get a good night’s sleep and come to class with your
thinking cap on!
|
|
|
W 10/28/09
|
No additional HW due.
In class: First half of video on fractals.
Quote of the day: “Think not of what you see, but what it took to produce
what you see”—Benoit Mandelbrot, as paraphrased. In other words, simple
parameter settings and simple rules can give rise to extraordinary
complexity.
|
|
|
Th 10/29/09
|
No additional HW due.
In class: Second half of video on fractals.
The power law for energy use says that E
= kM0.75, where E is energy consumption, M is organism mass, and k is a constant of proportionality
needed to make the units work out. Thus an elephant, which is about 200,000
times as massive as a mouse, needs only about 200,0000.75 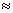 10,000 times as much
food energy to live. 10,000 times as much
food energy to live.
An important application of statistics is to be able to derive relationships
such as E = kM0.75 from data. In other words, given a large number
of points on a scatterplot, what function (a.k.a. “mathematical model”) can
be used to relate the two variables? You did some of this in precal last
year, and you will do more of it this year.
|
|
|
F 10/30/09
|
No additional HW due.
One or two small quizzes (10 pts. each) on recent material will be likely.
You are expected to have watched the entire video and to have read the
paragraphs in Thursday’s calendar entry. Quiz questions covering the video,
if any, will be “open notes.”
|
|