|
W 9/9/09
|
First day of class. Discussion of Mr. Hansen’s three rules, required equipment, fire
drill quizzes, what a statistic is, etc.
|
|
|
Th 9/10/09
|
HW due: Visit www.StudyOfPatterns.com/videos and
watch topics 3B and 4; send me a signed
e-mail.
|
|
|
F 9/11/09
|
HW due: Read pp. 1-11 of the textbook and make an
entry in your reading notes (following the format in the HW guidelines) summarizing
one important aspect of the course in a single sentence. Then write out
short answers to #1.1 and #1.2 on p. 11 and watch this inspirational
3-minute video by Dr. Arthur Benjamin.
Important: I still need e-mails
from Lyon and Paul. Please see my contact
information for the address.
|
|
|
M 9/14/09
|
HW due: Read pp. 12-19; write #1.10, #1.12, and the problem
below.
Problem: Consider a typical
histogram (as defined in class on Friday 9/11), a bar chart (as in Figure 1.5
on p. 17), and a dotplot (as in Figure 1.6 on p. 18). What are the
similarities and differences among these three chart types? Use words such as
categorical and quantitative as you write up your
answer.
|
|
|
T 9/15/09
|
HW due: Use the techniques you learned in
precalculus (STAT CALC 8) to find the line of best fit for the following (x, y)
data points gathered from class:
(47, 30.89)
(18, 15.53)
(16, 14)
(25, 18.9)
(32, 23.44)
(60, 40.44)
(72, 47.5)
Write your equation in the form 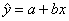 , where a and b are constants given by your
calculator. Use your equation, and show your work, in order to estimate (a)
the y-value when x = 52, (b) the x-value when y = 28.
Then (c) compute the correlation coefficient r, which your calculator displays for you when you do STAT CALC 8
if you have the Diagnostic On feature selected. (Otherwise, you can use VARS
to get the value of r.)
|
|
|
W 9/16/09
|
HW due: Play the correlation games (first and/or
second link in the list of Fun Links) until your skill level is good; read
pp. 27-31; write #2.4ab Note: In
part (b), provide at least two potential confounding variables.
|
|
|
Th 9/17/09
|
HW due: Read pp. 31-39 and answer the following two
questions. Note: Although your
textbook does not use the abbreviation, we will use the standard abbreviation
SRS throughout the course to mean simple random sample.
1. Explain, using clear language and complete sentences, why a sampling
procedure in which every 20th fan to enter through the main gate at Nationals
Park is surveyed does not generate an SRS of the fans who enter through that
gate.
2. Mr. Hansen has observed that there is an high correlation (greater than
.9) between homework quality and overall grades in his STAtistics class. Is
it valid to conclude that homework improves learning for STAtistics? Give several reasons to support your
answer.
|
|
|
F 9/18/09
|
HW due: On the middle of p. 46, cross out the
boldface word Randomization and
replace it with Random Assignment.
Then, read pp. 42-49, write #2.34 and #2.38, and answer the following
question.
(a) All blood donated in the U.S. is screened for the presence of HIV-AIDS
antibodies. Although the screening tests are quite accurate, Type I and Type
II errors do occur. Explain, using clear language that reveals an
understanding of the concept, what “Type I” and “Type II” would mean in this
context. Your answers must, therefore, contain the term HIV-AIDS.
(b) In part (a), which type of error would be more important to keep small,
and why?
(c) If you design a test that satisfies part (b) by minimizing one type of
error, what is the downside? In other words, what disadvantages would occur
as a result?
|
|
|
M 9/21/09
|
No HW due. This is the rarest of all events, a true
“fat tail” occurrence if ever there was one. Get lots of sleep, OK?
In class: Learn the Type I/Type II rap.
|
|
|
T 9/22/09
|
HW due: Read pp. 51-54, 65-66; write pp. 67-69
#2.58-2.68 even.
|
|
|
W 9/23/09
|
HW due (strongly recommended): Do the odd-numbered review
exercises on pp. 19-22, almost all of which have answers in the back of the
book. The “Quick Study” recurring assignment cannot occur this week because
the Post has apparently stopped
running this feature weekly. It is now appearing only sporadically in the
Health section.
|
|
|
Th 9/24/09
|
Test (100
pts.) on all material covered thus far. Sorry, but this is the best day for the test, hands down. Graham,
Nick, Robbie, and Arya are taking the test during D period in MH-102, Thomas
during E period outside MH-313, and Paul and everyone else at the usual class
time.
Our first test from last year
covered somewhat different material but is representative of the difficulty
and general format of my tests. If someone would like to send me an answer
key, I will correct it and post the answers for everyone to see.
|
|
|
F 9/25/09
|
Centennial day of community service (no class).
Arrive at school between 7:30 and 7:45 a.m. carrying a water bottle with your
name on it. Lunch will be furnished.
|
|
|
M 9/28/09
|
HW due: Read pp. 75-83, 87-92; write exercise 1
below. The reading assignment can be skimmed in places; you are not expected
to read every word.
1. Here are some actual scores from two STAtistics tests a number of years
ago. The students are in the same order in both data sets.
Test #1 {74, 84, 79, 94, 89,
79, 74, 84, 84, 69, 79, 89, 74, 79, 79, 63.5, 74}
Test #2 {74, 80.7, 70, 94,
102, 114, 94, 95.3, 74, 88.7, 74, 98, 88.7, 75.3, 76.7, 100.7, 63.3}
(a) Compute the sample mean and sample s.d. for test #1, using correct
notation to label your answers.
(b) Compute the 5-number summary for test #1.
(c) Sketch a boxplot (a.k.a. box-and-whiskers plot) for test #1.
(d) Are there any outliers for either data set? (We will use the “1.5 IQR
rule” as follows: Compute the IQR, multiply by 1.5 to get a value that we
will call “1.5 IQR,” and then see if any data points are more than 1.5 IQR
below Q1 or more than 1.5 IQR above Q3. If so, we will
call them outliers.)
(e) Compare the two tests by constructing a back-to-back split-stem plot,
similar to the example shown on p. 92, except with 2 stems for the 60s, 70s,
80s, 90s, and 100s, which you would label as 6, 7, 8, 9, and 10,
respectively. You need only one stem for the 110s, which you would label as
11.
(f) Adapt the segmented bar graph style (left half of Figure 3.6 on p. 81) to
compare the proportions of A, B, C,
and D grades on the two tests. In other words, you will need two segmented bars similar to the one
on the left. Label one of them “Test #1” instead of “Denials,” and label the
other one “Test #2.” Use the same 100% scale for both in order to allow
comparison.
(g) Compute the r value for a
linear model using student scores on one test as a predictor of the other.
Comment briefly on what you think a scatterplot would show.
(h) Sketch a scatterplot for the two tests. Does it conform to your
prediction in part (g)?
|
|
|
T 9/29/09
|
HW due: Write a proposal, approximately half a page long,
for a data-gathering exercise. When we form groups during class Tuesday, each
group will decide which proposal seems most interesting and best.
Your proposal must include the following:
Research question. For example,
“Do female high school students have different finger length patterns, on
average, compared to male high school students?”
Methodology description. How do
you intend to gather data? How will you guard against measurement error,
response bias, experimenter bias, and other foreseeable problems? How will
you ensure that all test subjects (if you are using human subjects) have been
treated ethically and have granted their consent?
Timeline. How long do you see this
project taking? There will be some class time available for administrative
meetings, but nearly all work will need to be performed outside of class. A
3- to 5-page project writeup, plus an appendix of raw data, is expected from
all groups. Do you want Mr. Hansen to comment on a draft of your writeup? If
so, build an extra two days into your schedule.
|
|
|
W 9/30/09
|
HW due: Propose a group formation methodology (for
project groups) based on random selection. Also, if your submission (if any)
from yesterday was not in compliance with proper format and content
requirements, please re-do it so that it measures up.
|
|