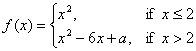Honors AP Calculus / Mr. Hansen	Name: _______________________________
10/8/2009	READ INSTRUCTIONS IN EACH PART! ______

Test #2 (100 points): No Calculator Allowed

	Part I: Mathematician Matching (2 points each, no partial credit) Write the capital letter of the best choice in the blank provided. Each choice is used exactly once.
___1.	Gödel	A. Faced a bitter rivalry with Newton over the issue of who had developed the calculus first
___2. ___3.	Weierstrass Mandelbrot	B. His name is attached to a self-similar set formed by removing the middle third from a line segment (usually the interval [0, 1]) and then recursively removing each middle third from the segments that remain
___4.	Koch	C. Noted for the snowflake curve, a self-similar curve having finite area but infinite perimeter
___5.	Leibniz	D. Shook the foundations of mathematics with his famous Incompleteness Theorem approximately 80 years ago.
		E. The only one of the six mathematicians listed here who is still alive
___6.	Cantor	F. Noted for defining a bizarre function that is continuous everywhere but differentiable nowhere
	Part II: Multiple Choice (3 points each, no partial credit, no penalty for guessing) Write the capital letter of the best choice in the blank provided.
___7.	Is the graph of the function mentioned in F above a fractal?
	(A) yes, because the function is differentiable		(D) no, because the function is not differentiable
	(B) yes, because self-similarity is evident		(E) no, because self-similarity is not evident
	(C) yes, because it is the Mandelbrot set
___8.	Most cellular telephones include what application of fractals?
	(A) fractal transmission patterns (B) fractal antennas (C) fractal 3-D integrated circuits		(D) fractal noise (E) fractal display software
___9.	In mathematics, the term parameter means . . .
	(A) a boundary		(D) a constant
	(B) the perimeter of a boundary		(E) an adjustable constant
	(C) a variable
___10.	In the formal definition of , what is the reason for using a punctured -neighborhood of c in the clause that says 0 < | x – c | < must imply | f (x) – L | < , instead of simply basing the definition on an open interval where x (c – , c + )?
	(A) An open interval is not a neighborhood of a point.
	(B) There is no good reason; an open interval would work just as well as a punctured -neighborhood, but there is a tradition in calculus textbooks of using both and in the definition of limit.
	(C) The question is posed incorrectly. The formal definition of limit requires the function values to lie within a punctured -neighborhood of L, i.e., the set of y values such that 0 < | y – L | < , where y = f (x).
	(D) We wish our definition to make no requirement that f (c) exists.
	(E) The question is posed incorrectly. The formal definition of limit requires the function values to lie within a punctured -neighborhood of L, i.e., the set of x values such that 0 < | x – L | < , where y = f (x).
___11.	When it comes to factual knowledge, most human beings . . .
	(A) greatly underestimate how much they know (B) slightly underestimate how much they know (C) are well calibrated (D) slightly overestimate how much they know (E) greatly overestimate how much they know
	Part III. Fill in the Blanks (9 points)
12.	Would Mr. Hansen say that arguing about math problems and solution procedures is a good way to learn? ___ Why or why not? _________________________________________________ Every calculus, whether it be the differential calculus, the _____________ calculus, or the calculus of logic, is a __________ system, by which we mean a ___________________________ ________________________________________________________________________ .
	Part IV. Problems (9 points each) Show your work. Cryptic or illegible responses, or responses with insufficient work, will not receive full credit.
13.	State the definition of derivative, and use the definition to compute for f (x) = 2x^2 − 3x + 2.

14.	Let
(a)	Prove that f is not continuous at x = 2 if a = 10.
(b)	Find the value of a that would make f continuous at x = 2.
15.	Let g(x) = 3^x. Given: g is differentiable on .
(a)	What kind of function is g? Circle all that apply:  exponential  power  polynomial  trigonometric
(b)	Prove, rigorously, that since 3^2 = 9 and 3^3 = 27, there exists a value of x such that 3^x = 10. What are the bounds on x?

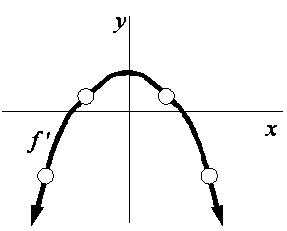
16-19.	For each graph of , sketch a plausible graph for f, or if that is impossible, provide 1-2 sentences of explanation.
16.
17.
18.
19.
	Part V. Very Silly Part (2 points)
20.	What does Mr. Hansen have in common with the Knights Who Say “Ni”?
	________________________________________________________________________
	________________________________________________________________________
	Part VI. Leftover Part (required for homework; did not make the cut for the in-class test)
21.	Prove that if ~P does not imply Q, then P and Q are both false. Show all steps, but you do not need to provide a reason for each step.