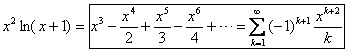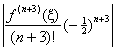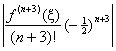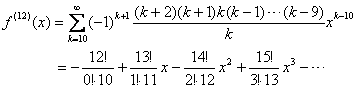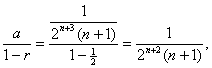Honors AP Calculus / Mr. Hansen	Name: _______KEY__________
5/21/2010

Another Quiz on Lagrange Error Term

1.	Use Taylor’s Theorem and/or general knowledge/cleverness to find a Taylor series for
	Take ln x =
	Formally substitute (x + 1) for x in the series above to get
	Multiply through by x^2 to get
2.	Use the result of #1 to determine how many terms are required to guarantee accuracy within .00004 when estimating . Use the Lagrange error bound.
	[The wording of this question was unfortunate. In retrospect, I realize that I should have worded the question as follows: “State the Lagrange error bound for if the series in #1 is used. Assess whether the Lagrange bound is useful in this context, and then determine, preferably by analysis, how many terms are required to guarantee accuracy within .00004 when estimating with the series you found in #1. Experimentation is encouraged but will not qualify for as much credit as analysis.”] In grading this quiz, I am providing leniency for anyone who at least stated the Lagrange error bound correctly, namely E = , where and The reason for using n + 3 instead of n + 1 is that f and its first two derivatives are always zero at x = 0, which means that the Taylor series starts out with a cubic first term. Some students even found the correct “bottom line” answer, 10 terms, by experimentation. I would have preferred some analysis—comparison to a geometric series is easiest—but will accept experimentation in view of the poor original wording of the question. Solution: Let E denote the absolute value of the Lagrange error term in this problem when . E is easy to evaluate with WolframAlpha.com but is essentially impossible to evaluate with a handheld TI calculator. Moreover, the bound on E is so conservative (e.g., .0527 after 17 nonzero terms of the Taylor series with ) that the Lagrange method is utterly useless for finding accuracy within .00004 as required. One would have to use thousands of terms, and even WolframAlpha fails in estimating E after about 120 terms. Therefore, we will be content with stating E, proving that E converges, and concluding that (at least in theory) E could be estimated accurately. For answering the question posed regarding the number of terms, we will use a simpler method that does not even require a calculator.
	Since , let and consider Note that since f and its first two derivatives are zero at x = 0, the Lagrange error bound after n nonzero terms is of form for some
	Bounding |f ^(n + 3)(x)| on the interval is difficult but not impossible. Trying to find a general form for f ^(n + 3)(x) by standard differentiation leads to an intractable mess. However, we can differentiate the power series in #1 term-by-term to get
	By writing out some terms, we can see clearly that the derivatives have maximum absolute value when . For example, consider n = 9 terms, which means that the Lagrange bound will involve a 12th derivative as follows:
	By inspection, this power series for f ^(12)(x) attains maximum absolute value on when . The power series for derivatives of all other orders are similar.
	The next step is to assemble the pieces for the Lagrange error bound, E.
	As noted above, there is no practical way to compute this on a TI calculator, even for small values of n, and though WolframAlpha.com handles the summation with ease (at least for values of n up to about 120), the bound is not tight enough to be useful.
	Convergence is easy to prove, however, and that would be a good exercise. Use the ratio method to prove that for any natural number n, converges. [Steps omitted; please do this.]
	Since the Lagrange bound is useless, what should we use instead? Several students observed that by direct computation, the 10-term partial sum given by
	is approximately −0.173266214037698, which differs from by only about 0.0000206. Thus 10 terms suffice. Although this is not a “sporting” way of coming up with the answer, I did accept it for this quiz because of the poor wording of the question as noted above.
	A more “sporting” approach that you should understand and appreciate is to observe that the series for looks a lot like a geometric series with first term and common ratio . Let a denote the absolute value of the first term not taken after adding up n nonzero terms. We have . Then the absolute value of the tail is strictly less than and the beauty of this bound is that it can be evaluated without a calculator! Remember, .00004 = . Here is a table:
		n = no. of terms
		_____________	_____________
		1
		2
		3
		9
		10
	Again, we have shown that 10 terms suffice in order to ensure accuracy within .00004.
	Other answers are possible. However, one thing you cannot do is to try to apply the AST procedures, because the series of constants created by plugging in x = does not alternate. Every term in the series is negative.