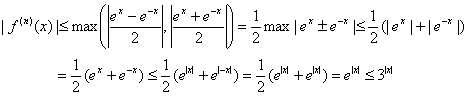|
Honors AP Calculus / Mr. Hansen |
Name: _______KEY__________ |
|
5/20/2010 [rev. 6/7/2010] |
|
Quiz on Lagrange Error Term
|
1. |
Prove: If f (x) = sinh x, then |
|
|
|
|
|
Note: For all
real numbers a, b, we know (or should know) that |
|
|
|
|
|
Since f (n) (x) is always either sinh x or cosh x, and since e is known to be less than 3, we have the following for all real x: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Use the result of #1 to find the maximum possible error
when the Maclaurin series for sinh
x is used to estimate sinh 4 with 6 nonzero terms. Warning: |
|
|
|
|
|
By Taylor’s Theorem, |
|
|
sinh x = f (x) = |
|
|
|
|
|
Note that all the even-numbered terms (0, 2, 4, etc.) are 0. Thus the Lagrange error bound after 6 nonzero terms is |
|
|
|
|
|
|
|
|
Since sinh x is positive and increasing on (0, 4) [considered known, but easily proved by observing that sinh x has a derivative, cosh x, that is positive everywhere], |sinh x| is bounded on (0, 4) by sinh 4, and by #1, we know that a bound for sinh 4 is 34. |
|
|
|
|
|
Therefore, |
|
|
|
|
|
Several students made use of the fact that all even-numbered terms in the Maclaurin expansion are zero. Therefore, we might as well say that we have used 12, not 11, terms in achieving the first 6 nonzero terms. The advantage of doing that is that then the “n + 1” in the Lagrange error term can be 13 instead of 12. This gives a bound of |
|
|
|
|
|
|