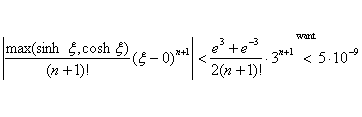|
|
Spring break.
Confidential to anonymous e-mailers: Thank you for your words of support.
|
|
|
M 4/5/010
|
HW due: As we discussed on Friday 3/19, I would like
you to begin reviewing for the AP exam. Please make a hard copy printout of
this 2-page review log so that you can
keep a written record of your study progress during spring break. Since it is
a break, I obviously do not expect you to work 35-45 minutes per night, but
when we return, I would expect to see some
written evidence on the log sheets showing that you have begun your AP review
in earnest.
An investment of as little as a few minutes per day, if you are consistent,
will pay huge dividends when we get to the AP exam in May. Be sure to get
plenty of sleep also!
Another resource that you may find helpful is this BC topic list, which I have laboriously
cross-referenced against the sections of our textbook. Of course, you may
prefer your textbook’s index, and that is certainly your choice. At any rate,
it is important for you to know exactly which topics are fair game for the AP
exam and where to go in your textbook if you need more practice on any of
them.
I would also encourage you to read this essay, which
should be quick and enjoyable. The essay will eventually be required reading
for everyone, but I will delay making that formal assignment until after the
AP exam.
|
|
|
T 4/6/010
|
HW due: Read §12-3; write §12-2 #2, 7, 8, and as
many of the problems in §12-3 (#1-11 all) as time permits. We will cover the
remainder in class.
|
|
|
W 4/7/010
|
HW due: Finish writing §12-3 #1-11 all; read §12-4;
write §12-4 #2, 3, 4, 6, and a definition of “solution” and “human being.”
In class: Lockdown incident until approximately 9:23 a.m.
|
|
|
Th 4/8/010
|
HW due: §12-5; write §12-5 #9, 12, 13, 14, 15-33 mo3.
The first four of these should go very quickly. If you cannot finish all of
these because of our disrupted class yesterday, I understand; however, you
can still do many if not all of these. For example, in #12, all you have to
do is replace all occurrences of x
in the familiar cosine series with x2,
and simplify slightly.
|
|
|
F 4/9/010
|
HW due: Read §12-6; write §12-6 #1, 4, 7, 12, 13,
14, 15, 17, 19.
“Regurgitation” Quiz (10 pts.) on the 8 standard Taylor series (p. 616) and
their intervals of convergence. The intervals of convergence are the real
line for all except the last three listed:
- The series for ln x converges only on (0, 2].
- The series for 1/(1 – x) converges only on (–1, 1).
- The series for arctan x converges only on [–1, 1].
|
|
|
M 4/12/010
|
HW due: Read the green boxes on p. 630 and all of
§12-7; write §12-6 #22, 23, 25, 26. Note: The root technique is not on the AP
exam.
|
|
|
T 4/13/010
|
HW due: Read the green box on p. 640 and all of §12-8.
Also, please check your work for §12-6 #26,
the 5-minute-long problem that I foolishly attempted to do in the final 30
seconds of class. There is no additional written work due (other than your
daily AP review, of course, which you should be continuing).
In class: Review for test. Bring your questions!
Also during class: Pop quiz on series.
|
|
|
|
The following anonymous e-mail was received with timestamp
20100413 2025 EDT:
Wouldn't the first three terms for the example MC (e^2) be: 1 + 2 + (2^2)/2!,
so a third-degree Taylor polynomial would include these terms and simplify to
3 + (2^2)/2! ?
Answer: The third-degree Taylor
polynomial for ex is the
approximation 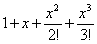 , ,
since we need to include all terms through the third power of (x − a), where a denotes the
value about which the series is expanded. “Degree” does not refer to the number
of terms, nor even to the number of nonzero terms, but rather to the highest
power of the polynomial. Note that a
= 0 here, since we are using the standard Maclaurin series for ex. The value of the polynomial, when used to
estimate e2, is
therefore 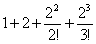 , which is choice E. , which is choice E.
|
|
|
W 4/14/010
|
“Air
Handler” room: Test (100 pts.) through §12-6, including the AST convergence
principle hinted at in §12-6 #17.
Format of this test will be as follows:
- One AP free-response question comparable in
difficulty to #6
from the 2008 Form B exam. This question, which should take you
about 15 minutes, will be curved and counted for 30% of your grade.
- Approximately 5-7 AP multiple-choice questions
comparable to the sample given below. These questions, which should take
you approximately 14 or 15 minutes, will be curved and counted for 30%
of your grade.
- The remaining 40% of your grade will be short-answer
and straightforward questions based on classroom discussion and textbook
homework. These questions will be scored on a straight scale (no curve)
- Time
management: The first 15
minutes will be for the AP free-response question. You will not have the
multiple-choice questions available for viewing during this time. The
next 14 or 15 minutes will be for the AP multiple-choice questions (2
minutes per question if they are “without calculator,” 3 minutes per
question if they are “with calculator”). In the unlikely event that you
have extra time during the multiple-choice portion, you may go back to
the free-response question without penalty. Both AP portions will then
be collected and replaced with a set of non-AP questions, and you will
spend the remaining 20 minutes of the period working on those.
Bring your calculator, but be aware that many problems on the AP exam
(including #6 linked above) do not permit a calculator to be used, even
though there is computation involved. Part (d) of that question requires
familiarity with the principle that for an alternating convergent series
whose terms are decreasing in absolute value, the error after n terms is bounded by the absolute
value of the first omitted term. This principle, which is not formally
presented in your textbook until §12-7 (p. 634), is hinted at in §12-6 #17
and is therefore considered “fair game” for this test.
Sample
multiple-choice question:
The value of the third-degree Taylor polynomial about x = 0 that approximates e2
is . . .
(A) 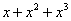
(B) 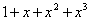
(C) 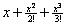
(D) 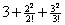
(E) 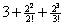
Since many of you have a history test today, you will be allowed to take the
test tomorrow if you prefer. Important:
You need to report for roll call at 8:00 unless you have made special
arrangements with me, preferably face-to-face. Sending an e-mail does not
qualify unless you have also received a reply from me.
Answer to sample question: E.
|
|
|
|
A blank copy of most
of yesterday’s test is available. The missing questions, questions 2 and
3, came from this
link (see pp. 30 and 32) and cannot be posted on our website.
|
|
|
Th 4/15/010
|
“Air
Handler” room: Optional re-test, same coverage and same format as yesterday. Since many of you have a biology test today, you
may wish to skip this test if you feel you did fairly well yesterday.
However, you still need to report for roll call at 8:00 unless you have made
special arrangements with me, preferably face-to-face. Sending an e-mail does
not qualify unless you have also received a reply from me.
If you wish to take both tests, then only the higher score of the two will
count toward your quarter average.
For those of you who are enrolled in both U.S. history and AP biology, I
apologize for the fact that you will have 3 or 4 tests yesterday and today.
However, this is within the 2-per-day limit that is authorized under STA
policy, and hopefully the fact that you have some flexibility with your
HappyCal tests will make things more manageable for you.
|
|
|
F 4/16/010
|
HW due: Print out Wednesday’s test and correct it
completely. You may work with friends, but each student must write his own
answers (i.e., no direct copying). Arguing is encouraged!
You may omit questions 2 and 3 from the homework assignment, since the
answers to those two are already posted at this
link (see pp. 30 and 32).
Please record the time you spend on this assignment on your AP review log.
|
|
|
|
Announcement: Please click here for news of two upcoming
math lectures in downtown DC. The second one, on the subject of math and
music, looks particularly interesting, and I will be attending. Maybe I could
get a contingent of HappyCal students to join me on April 27.
|
|
|
M 4/19/010
|
HW due: Write §12-7 #5-14 all, extra problem
(below), and optionally 25-30 all. The first group (#5-14 and the extra problem)
are the most important, since they are the most similar to AP problems.
Solutions to the others are given below, but please refer to them only if you
get stuck. Try to do as much as you can before you give up!
Extra problem: For the test
problem, cosh(−2), determine how many terms are needed in order to
ensure an error of less than .0001. You can use a “sloppy” error bound of 3
as an upper bound for e when
performing your analysis. Use the Lagrange error bound taught in class last
Friday, but be careful! Counting the terms can be tricky.
Solutions to all other problems:
25. Since this is a geometric series with common ratio r = 1/4 satisfying | r
| < 1, the series converges.
26. Much as in #25, this is a geometric series with r = 3/4, which satisfies | r
| < 1. The series converges.
27. The first term, in which n = 0,
is a term having value 1 with no effect on convergence. All other terms are
positive and are bounded above by 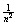 . Therefore, the series converges by comparison to a
p-series with p = 2. Or, if you prefer, you could say that the terms are all
bounded above by . Therefore, the series converges by comparison to a
p-series with p = 2. Or, if you prefer, you could say that the terms are all
bounded above by 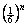 , implying convergence by comparison to a geometric series
with r = 1/6. , implying convergence by comparison to a geometric series
with r = 1/6.
Loose end for #27: If anyone doubts that the “nth term” (by which we mean the term indexed by n, or technically the (n + 1)st term of the series) is
bounded above by 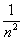 for all n > 0, then here is a sloppy but
valid proof: for all n > 0, then here is a sloppy but
valid proof:
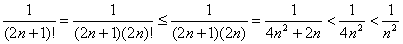
28. This is a convergent geometric series with r = –1/3, which satisfies | r
| < 1. Or, if you prefer, use AST instead.
29. Since 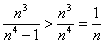 , ,
each term is bounded below by the corresponding term of the harmonic series.
Since the harmonic series diverges, the given series also diverges.
You could also use the integral test or the limit comparison
test. The limit comparison test is not covered in our textbook, nor is it
a requirement for the AP exam, but it is one of the most useful tests
available, since it can save you from the tedious inequality-crunching that
often accompanies other comparison tests.
30. Series diverges by the nth
term test. (The limit of the nth
term is not 0 as required for convergence.)
|
|
|
T 4/20/010
|
HW due: Write #25-30 that were assigned last week
(with solutions above in case you get stuck), plus the following additional
problems.
Additional problem 1: Construct a
series that satisfies all the conditions of the AST except for the part about
monotonically decreasing absolute value. Show that such a series need not
converge.
Additional problem 2: Show by
direct computation that 6 terms of the cosh x Maclaurin series suffice to provide accuracy within .0001 of
the true value. Note: Please
correct your notes from yesterday to reflect this fact. I did all of the work
correctly, including the table of n
and bounds for the Lagrange error term, but I mistakenly failed to mark n = 5, with a bound of .000026, as
success. Taking n = 5 means that 6
terms are required (not 7 as I stated before Chen and Sunil spotted the error
as people were leaving).
Additional problem 3: Compute the
number of terms required to calculate the sine of 0.8 radians within an error
tolerance of .000001. Do this two ways: (a) by using the AST, showing all
verification steps, and (b) by using the Lagrange error term.
Additional problem 4: Send me an
e-mail in which you state whether you will attend next Monday’s practice AP
exam at 8:00 a.m. To sweeten the pot, I will waive the final exam requirement
for anyone who does reasonably well on the practice exam. Seniors who have a
B average or above (and who are therefore already exempt) can choose whether
to apply or not to apply the results of the practice exam to help their
grade. Underclassmen will also have the choice to use the score in averaging
or not.
|
|
|
W 4/21/010
|
HW due: §12.8 #2-6 all, 11, 13, 14. The solution for
#6 is given below, and you are encouraged to refer to it. Hint for #13: Draw a picture.
Note
regarding yesterday’s “Additional problem 3”: As people were filing
out of the room, one student asked why we could not use a Lagrange error
bound with exponent and derivative of order 2n + 3, instead of the 2n
+ 2 that I actually used. The answer is that since you know that the (2n + 2) derivative will be 0, you can
safely use 2n + 3 in your Lagrange
error term. And, when you do, you will find that n = 3 is the first value that works, which means that 4 terms
are necessary for the required 10−6 error tolerance. The
method that I used gives a more conservative answer of 5 terms. By the way,
when you have a choice of which error term to use, always choose the AST
method, since it (as illustrated here) will generally give a tighter error
bound with less fuss.
Solution
to §12-8 #6:
cosh 3 = 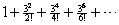 , where the terms are numbered according to the exponent.
“Real” term 1 has exponent 0, “real” term 2 has exponent 2, and so on. As n goes from 0 to , where the terms are numbered according to the exponent.
“Real” term 1 has exponent 0, “real” term 2 has exponent 2, and so on. As n goes from 0 to 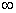 , the real term number (let us call it q) equals half the exponent, plus 1. In other words, , the real term number (let us call it q) equals half the exponent, plus 1. In other words, 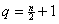 . .
Let f (x) = cosh x and a = 0, thus giving Lagrange error term
of form 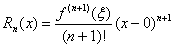 . .
Since the derivatives of sinh x are
all either sinh x or cosh x, an upper bound for |Rn(x)| when 0 < x <
3 would be
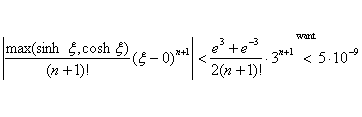 . .
The rationale for wanting the expression to be less than 5 · 10–9
is that 8 decimal places of precision will generally be ensured [see note
below] whenever the error is less than half of a unit in the 8th decimal
place, i.e., 0.5 · 10–8 or, equivalently, 5 · 10–9. The
easiest way to solve the inequality is to put the function
(e^3+e^(–3))/2/(X+1)!*3^(X+1)
into the Y1 function on your calculator. Then push 2nd TBLSET and
set TblStart=1,  Tbl=1, Auto, Auto. When you push 2nd TABLE, the values will
all be displayed for you. Scroll down to see the first value for which the Y1
expression is less than 5 · 10–9, namely 20. Tbl=1, Auto, Auto. When you push 2nd TABLE, the values will
all be displayed for you. Scroll down to see the first value for which the Y1
expression is less than 5 · 10–9, namely 20.
[Note: Because there are certain
pathological cases where having error less than 5 · 10–9 does not
guarantee 8 digits of displayed accuracy, the AP exam does not pose questions
in this format. Instead, you will see a much more straightforward demand. For
example, you may be asked to compute the number of terms needed in the
partial sum in order to guarantee an error less than .001. That is a much
easier question, since you simply take whatever value is given to you and put
it on the right side of your “want” inequality.]
What does n = 20 mean? It does not mean 20 terms. What it means is
that 20 is the first n value that
ensures an error term less than 5 · 10–9 in absolute value. By our
rule above, the term number is found by 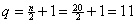 . .
Final answer: The partial sum must have 11 terms.
If you wish, you can cross-check your work by computing partial sums as
follows:
Press MODE and select Seq instead of Func.
Press 2nd QUIT.
Press the Y= key.
Set nMin=0,
u(n)=u(n–1)+3^(2n)/(2n)! by using the 2nd function of 7 to
get u and the “ ” key to get n. ” key to get n.
Set u(nMin)={1}.
Press 2nd QUIT.
Key in 2nd CATALOG D uparrow uparrow uparrow uparrow ENTER 3 ENTER to compute
cosh 3, namely 10.067662. (The actual value, which your calculator does not
show you, is 10.06766199578 . . .)
Key in u(1) ENTER to compute the 2nd partial sum, namely 5.5. This is, of
course, nowhere close to cosh 3.
Key in u(2) ENTER to compute the 3rd partial sum. Not much better!
Key in u(2)–cosh(3) ENTER to compute the error after the 3rd partial sum,
namely –1.192661996. No good!
Key in 2nd ENTRY and modify to get u(9)–cosh(3) ENTER. This gives the error
after the 10th partial sum, a very respectable –1.461 · 10–9. Now,
you might think that this would be enough to guarantee 8 places of accuracy,
but unfortunately here it does not. The issue is not whether the actual error
is less than 5 · 10–9, but rather whether the Lagrange error bound
can be guaranteed to be less than 5 · 10–9. The latter does not
occur until after the 11th partial sum, namely u(10).
Key in u(9) ENTER and notice that the 10th partial sum does not exactly equal
cosh(3). In fact, u(9), which is the 10th partial sum, displays as
10.06766199 to 8 places, while cosh(3) displays as 10.06766200 to 8 places.
The difference is caused by the small discrepancy in the 9th decimal place as
computed above.
Finally, key in u(10) ENTER to find the 11th partial sum. Now we have an
answer that agrees with cosh 3 to 8 decimal places. Whew!
|
|
|
Th 4/22/010
|
HW due: Keep working on the §12-8 problems, and (if
possible) correct and score your 4/14 test corrections by referring to the
key posted below. Also do a few AP review problems, as always.
4/14 scoring key: page 1 page 2 page 3 page 4 page 5 page 6 page 7
I had a number of technical difficulties with the scanning, and I apologize
for the delay in posting the scoring key. Because of the late posting hour, I
cannot require you to have the corrections complete until Friday.
How
to convert your AP scores in Part I: The free-response questions have
9 points possible. Each point is indicated on the key by a large red blob.
There is no partial credit. To convert your raw score (0 to 9) to an
appropriate number of scaled points, use the formula 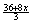 , where x = raw
points. For example, if you earned 3 out of 9, then your scaled score would
be (36 + 24)/3 = 20 points on the test. That equates to a D+ for Part I,
since 30 points were possible. , where x = raw
points. For example, if you earned 3 out of 9, then your scaled score would
be (36 + 24)/3 = 20 points on the test. That equates to a D+ for Part I,
since 30 points were possible.
How
to convert your AP scores in Part II: As for the multiple-choice
questions, there were 7 questions worth 4 points each, with 0 for an omission
and −1 for each incorrect answer. The answers to #2 and #3 are
available at the link given on the key: #2 is question #13 on page 32 of this
link, and #3 is question #9 on page 30 of the
same link. To convert your raw score (−7 to 28) to a scaled score,
you would use the formula 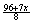 , where x = raw
points. For example, if you had 4 questions correct, 2 wrong, and 1 omission,
your raw score would be 4(4) + 2(−1) + 1(0) = 14 points, which becomes
24.25 points on the test. That equates to a low B for Part II, since 30
points were possible. , where x = raw
points. For example, if you had 4 questions correct, 2 wrong, and 1 omission,
your raw score would be 4(4) + 2(−1) + 1(0) = 14 points, which becomes
24.25 points on the test. That equates to a low B for Part II, since 30
points were possible.
Scoring
in Part III: Scoring in Part III requires a little more judgment
since there is no AP-style rubric. Point values are indicated in parentheses
in the left margin, and no conversion formula is required. Simply add up the
points.
|
|
|
F 4/23/010
|
Announcement:
Today’s class will take place in the “Air Handler Room” (MH-001).
HW due: Score your April 14 test using the key posted in yesterday’s calendar
entry, finish all previously assigned problems in Chapter 12, and work some
AP review problems, as always.
Quiz will cover the BC Calculus
Cram Sheet. (See “Links for AP Preparation” area of HappyCal Zone page.)
|
|
|
|
Here are some useful materials for you to look at
over the weekend:
All tests will be available for you to look at and take with you on Monday
morning. A detailed score report was e-mailed to you on Sunday, 4/25..
|
|
|
M 4/26/010
|
Save the
date! Practice full-scale AP examination, MH-212, 8:00 − 11:30. I sincerely hope that everyone can make it. Two
years ago we roused one of the dorm students out of a sound sleep when he
forgot to show up at 8:00 a.m. He went on to score a 5 on his real exam.
If the building is locked, I will try to station someone on Senior Circle
beginning at about 7:45 to let you in.
Bring: Calculator, spare batteries, several sharpened pencils, and a blue or
black pen for signing your name. Be sure to eat something before you come. No
food is allowed during the exam, but you should bring a snack for the break
time. LEAVE YOUR CELL PHONE IN YOUR
CAR OR IN YOUR LOCKER. YOU ARE NOT ALLOWED TO MAKE PHONE CALLS OR SEND TEXT
MESSAGES OR E-MAIL, EVEN DURING THE BREAK. THIS IS AN AP RULE THAT YOU NEED
TO PRACTICE. In the event of a true emergency, I will of course allow you
to borrow my cell phone.
You do not need a giant eraser, since you are allowed to write “X” on any
sections you wish to be ignored by the grader.
Review of instructions / bubble sheet setup, 0800-0803.
Part IA: Multiple choice, 28 questions in 55 minutes, no calculator,
0803-0858.
Part IB: Multiple choice, 17 questions in 50 minutes, calculator required,
0858-0948.
AP survey questions (required): 4 questions in 3 minutes, 0948-0951.
Comfort break, 0951-1001. Snacking is encouraged, but you will need to go
outside or to the refectory.
Part IIA: Free response, 3 questions in 45 minutes, calculator required,
1001-1046.
Part IIB: Free response, 3 questions in 45 minutes, no calculator, 1046-1131.
You may continue to work on Part IIA (however, without calculator) during the
time allocated for Part IIB. All time limits will be strictly enforced in
order to provide you with a good “cognitive map” for the real exam.
Ten-minute warnings will be given before the end of Part IIA and Part IIB.
However, you must track your own time during Part IA and Part IB. A clock
will be visible in the room.
IMPORTANT! During the break, just
as with the real AP exam, the rules are as follows (quoting from the AP
instruction book): “You are not allowed to consult teachers, other students,
or textbooks about the exam materials during the break. You may not make
phone calls, send text messages, check e-mail, access a computer, calculator,
cell phone, PDA, MP3 player, e-mail/messaging device, or any other electronic
or communication device.” Wow! In the event of a true emergency, I will of
course allow you to borrow my cell phone.
|
|
|
T 4/27/010
|
Class will start at 8:20 today. I will not start
deducting late points until 8:25.
Evening Event: Please click here for news of a math lecture
in downtown DC, on the subject of math and music. I will be attending, and I
hope to see a few of you there.
|
|
|
W 4/28/010
|
Class will start at 8:20 again today (8:25 for
latecomers). Please bring your revised free-response writeups so that you can
score yourself when I distribute the grading rubrics.
|
|
|
Th 4/29/010
|
HW due: Rewrite at least 2 of the 6 free-response
problems from Monday’s practice exam. Bring your writeups and your green and
blue exam booklets to class.
Class will start on time today
because of the Close security perimeter for the funeral of Dorothy Height.
The first 10 minutes of class will be set aside for you to argue with your
podmates about the correct multiple-choice answers. Appoint a team captain,
who will submit a complete set of answers (1-28, 76-92) to Mr. Hansen for
instant grading. Each of the top 3 pods will win a large Cadbury bar,
suitable for sharing. The other 3 pods will win only the knowledge that comes
through arguing over important questions, but that’s still quite a lot.
Ties, if any, will be resolved by a spelling bee.
|
|
|
F 4/30/010
|
Class will start at 8:10 a.m. today.
HW due: First, we will see how many people have rewritten at least 4 of the 6
free-response problems. (This will count as your homework grade for yesterday
and today.) Pods will be combined into “superpods” of 5 or 6, and each
superpod will spend the first 15 minutes working all 6 problems separately,
then 15 minutes editing and arguing over the writeups. (The strongest team
member may have to do 2 problems.) All writeups must be submitted on standard
AP-style response sheets that will be distributed during class.
Scoring rubrics will then be passed out, and the winning superpod will be
determined over the weekend.
|
|