|
M 3/1/010
|
HW due: Read §§10-3 and 10-4 (reading notes
required, as always), and work through this related rates tutorial.
Here are the steps required for the tutorial:
1. Read the text (approximately 4 screens’ worth when you scroll down).
2. If anything strikes you as worthwhile from the reading, add it to your
§10-4 reading notes.
3. Click on the tutorial link marked “Problem Sets” either at the top or at
the bottom of the page (both go to the same place).
4. Write up the two problems found there as if they
were regular homework problems. If you are not familiar with the rules of
baseball, you should ask a classmate for help. I also recommend #5 on p. 520
for another similar example that has answers in the back of the book.
5. After you have finished, click on the “Answers” link. Use a red pen or
some other distinguishable color to correct your answers.
Also, regarding the multiple-choice test questions . . .
If your multiple-choice answers from the two most recent tests contain any
errors, I will send you an e-mail by Sunday evening so that you can make
another submission on Monday. If there are no errors, I will merely need to
spot-check your work on Monday.
|
|
|
T 3/2/010
|
HW due: Read §10-5; write §10-3 #15, §10-4 #4, 9.
|
|
|
W 3/3/010
|
HW due: Read §10-6 (no reading notes required, but do
the “Q” problems on p. 530 in your head); write §10-5 #1-4 all, §10-6 #6, 10.
|
|
|
Th 3/4/010
|
HW due: Read §10-7 and #14 on p. 546, perform the
four housekeeping exercises below, and clean up all previously assigned
written problems. (We will use the result of #14 extensively. Feel free to
attempt to prove it if you wish, but that is not required for now.)
1. Use ink to correct the following typographical error on p. 536. In the
equation for 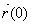 , the equation should be , the equation should be 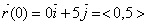 . .
2. Place the following in your reading notes: “We will use the shorthand
notation <a, b> to refer to the vector 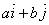 . This is standard, acceptable AP notation. For example, we
will usually write <3.5, −6.8> instead of . This is standard, acceptable AP notation. For example, we
will usually write <3.5, −6.8> instead of 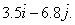 ” ”
3. We will consistently use the “double-bar norm notation” instead of the
single-bar notation used in the textbook. Write this in your reading notes:
“We will always write 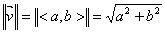 , where , where 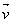 is the vector given
by <a, b> in component notation.” is the vector given
by <a, b> in component notation.”
4. Place the following in your reading notes: “It can be shown that 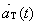 , the tangential component of the acceleration vector at
time t, is given by the formula , the tangential component of the acceleration vector at
time t, is given by the formula
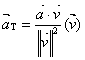 . .
This formula is acceptable for use on the AP exam. Since 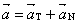 , we also know that , we also know that 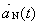 , the normal component of the acceleration vector at time t, is given by the formula , the normal component of the acceleration vector at time t, is given by the formula
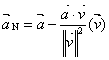 . .
In these formulas, 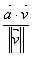 is the scalar
projection of is the scalar
projection of 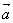 upon upon 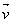 , and , and 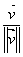 is a unit vector in
the direction of is a unit vector in
the direction of 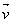 . .
Premultiplying that unit vector by the scalar projection (which may be
positive or negative) simply scales and directs 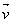 in order to produce in order to produce 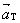 .” .”
|
|
|
F 3/5/010
|
HW due: Write §10-7 #1, 2. Make large, accurate diagrams.
Photocopies are not required, but if your graphing abilities are limited, you
may find it more time-efficient to use a photocopy.
|
|
|
M 3/8/010
|
HW due: Write §10-7 #13, 14; read §§11-1 and 11-2, especially
Example 2 on pp. 559-560. (Example 2 is a standard AP-type problem.) Use the
remainder of your time to clean up the assignment due last Friday, using
better-quality sketches.
An anonymous e-mail, which arrived with timestamp 20100308 0906 EST, objected
to the scheduling of Wednesday’s test. I myself would prefer to have the test
Thursday, but since there is a U.S. history test Thursday, I thought
Wednesday made more sense. For anyone who prefers to take the test Thursday,
I will provide a similar test from 7:00 to 7:45 on Thursday morning in
MH-102. I hope this compromise is acceptable to a majority of the class. [Note: On 3/9, we voted as a class to
hold a second optional test on Thursday.]
|
|
|
T 3/9/010
|
No additional HW is required. The following review
problems are suggested:
#5
from 2003, regular administration (no calculator allowed)
#3
from 2003, Form B (calculator required)
#4 from 2003, Form B (no calculator allowed): use same link as for #3
I recommend that you set a timer for 45 minutes and attempt to do all of
these problems. We will go over them in class.
|
|
|
|
We covered all the answers for #5 in class Tuesday.
Here are the answers for #3 and #4:
3.(a) 
(b)
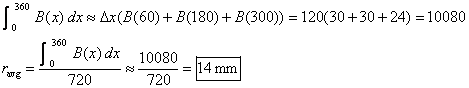
(c) For the portion of the blood vessel between 125 and 275 mm
from the designated start point, the expression represents the volume in mm3.
Units are required for full credit.
(d) On [60, 180] and again on [240, 360], B(x) has an average
change of 0. Since B(x) is twice differentiable, both B and 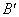 satisfy the MVT
hypotheses (cont. on closed int., diff. on open int.) throughout [0, 360]. By
MVT, there is at least one x = a in (60, 180) and at least one other x = b in (240, 360) such that satisfy the MVT
hypotheses (cont. on closed int., diff. on open int.) throughout [0, 360]. By
MVT, there is at least one x = a in (60, 180) and at least one other x = b in (240, 360) such that 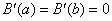 . Now, apply MVT to the function . Now, apply MVT to the function 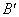 on the closed
interval [a, b]. Since the average change in on the closed
interval [a, b]. Since the average change in 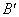 over [a, b]
equals 0, there is at least one x =
c in (a, b) such that over [a, b]
equals 0, there is at least one x =
c in (a, b) such that 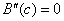 . Since (a, b) is a subinterval of (0, 360), c is within (0, 360) as claimed. . Since (a, b) is a subinterval of (0, 360), c is within (0, 360) as claimed. 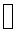
4.(a) <6e3t − 7e−7t,
9e3t + 2e−2t>, which has magnitude 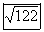 when t = 0 when t = 0
(b) 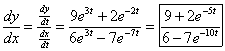 , which has limit 1.5 by inspection as , which has limit 1.5 by inspection as  [no L’Hôpital
needed!] [no L’Hôpital
needed!]
(c) Horizontal tangent implies 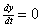 , which is impossible since 9e3t + 2e−2t > 0. (An exponential expression with positive base is
always positive, regardless of the exponent.) , which is impossible since 9e3t + 2e−2t > 0. (An exponential expression with positive base is
always positive, regardless of the exponent.)
(d) It is not usually
as easy as finding the places where 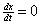 , since the limiting value of , since the limiting value of 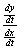 could be a real
number even if the denominator is 0 somewhere. However, by part (c) we know
that the numerator, could be a real
number even if the denominator is 0 somewhere. However, by part (c) we know
that the numerator, 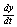 , is always > 0. Thus in this problem a vertical tangent
will occur iff , is always > 0. Thus in this problem a vertical tangent
will occur iff 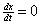 . Algebra gives . Algebra gives 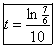 . [Note: For full
credit, you need to explain why finding where . [Note: For full
credit, you need to explain why finding where 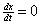 is sufficient in
this problem, since usually the analysis is more difficult, and you need to
show your algebra.] is sufficient in
this problem, since usually the analysis is more difficult, and you need to
show your algebra.]
|
|
|
|
The following anonymous e-mail was received with
timestamp 20100309 2257 EST:
Mr. Hansen, While doing review problems, I have been tripped up twice by similar
ambiguous questions. They read as follows: "Find the acceleration vector
and the speed of the object at time t = 1." What is confusing is whether
they want both the vector and the speed found at t = 1, or whether they want
the speed at t = 1 and the acceleration vector. (Upon checking the answers,
they want both at t =1) Am I missing something grammatically that indicates
what they want? Thanks
Answer: This reminds me of a story
my mom told me. When she was a schoolgirl, one of her Latin tests had instructions
that read, “Translate and give constructions of the underlined words.” What
the teacher meant to write, of course, was this: “Translate the passage, and
then give constructions of the underlined words.” My mother, a recent
immigrant from Germany, complied with the instructions as written and
proceeded to fail the test, since she did a much shorter version than what
the teacher had intended.
In your case, the instructions should be interpreted literally, and the
absence of a comma or other pause after the word “vector” means that the
prepositional phrase “at time t =
1” should apply to the entire foregoing text. AP questions are pilot tested
extensively, and it is rare for a typo (even in punctuation) to make it into
the final version. If the authors had intended for the acceleration vector to
be computed in terms of t, as
opposed to being “plugged in” for t
= 1, they would have requested that very clearly, as was done in the #4
problem from your suggested review problems.
Note, however, that since the questions in the review books are not tested
and edited as thoroughly, you may see some ambiguities from time to time.
During the real exam, as well as during our dry run on April 26, you will
have to make your best guess at what the was intended, since no questions can
be answered while testing is in progress.
|
|
|
W 3/10/010
|
Test (100
pts.) through §11-2. Roll call
check-in is required for all students, but if you are certain you will be on
campus Thursday, you are not required to take today’s test. Format will be AP
free-response, 3 multi-part questions in 45 minutes. The questions will be
either all “calculator required” or all “calculator prohibited,” but I will
not announce that decision in advance.
The problems will deal with work, average value, vectors, optimization,
related rates, and other similar topics. Some topics from earlier chapters
(e.g., differential equations, parametric arc length) may also make an
appearance. The optional review problems suggested for yesterday’s class are meant
to illustrate the type and difficulty you should expect.
|
|
|
|
Questions 1 and 2 on Wednesday’s test were, I hope,
straightforward. The first was a less-than-hard vector problem, and the second
was a basic related rates problem with trigonometry involved. However, the
third problem (which was #5 from the 2004 exam) has an answer
key and scoring guide that I encourage you to look at.
|
|
|
Th 3/11/010
|
Optional
Test (100 pts.) through §11-2. Roll
call check-in is required, but after that, you may use the time to study for your
history test if you prefer. The format will be identical to yesterday’s,
except that the calculator state may or may not be the same. If you take both
tests, the higher score will count. If you choose to skip one of the tests,
or if you miss one test because of illness or a similar reason, then the
other test will count.
|
|
|
F 3/12/010
|
No additional HW due.
In class: You will watch the Simpson’s
Paradox video (topic #1 from Mr. Hansen’s video collection). A quiz
Monday covering the video is possible. If you are absent today, you are still
responsible for viewing and learning the content of the video.
Update as of 1:19 p.m.:
I have been informed by e-mail that class was cancelled because the room was
locked (and apparently nobody thought to suggest to Mr. Casertano that the
Air Handler room was available as an option). That is OK; presumably you had
other classes you could study for during the period. We will still plan to
have a quiz Monday on the video, so be sure to watch it over the weekend.
|
|
|
M 3/15/010
|
HW due: Prepare for a quiz on the video whose link
is posted in the 3/12 calendar entry; write problem
#2 from 2007 Form B and problem
#5 from 2003 Form B, which were the two College Board-produced problems
from Friday’s test. Set yourself a time limit of 30 minutes for working the
problems, and then spend a few more minutes comparing notes with classmates
or online resources. I do not consider it cheating to check the scoring keys,
provided you first do the work
yourself, carefully documenting what portion is yours and what portion
(preferably in a different color) came from checking the key. The scoring
keys and a huge collection of problems from earlier years are available here,
but beware! I do not want you to visit that link before doing the problems
under a strict 30-minute time limit. (That would be cheating, really, plus it
would eliminate most of the educational benefit.)
|
|
|
T 3/16/010
|
HW due: Because of a technical glitch in posting the
assignment on time, this work is not due until Wednesday.
Read §11-3; write §11-3 #1, 3, 4, 6, 9, 12. For #12, use 6400 km or
640,000,000 cm as your approximation for Rearth.
A good approximation for Mearth
is 6 · 1027 g (so that you know what you are shooting for).
|
|
|
W 3/17/010
|
HW due: Do yesterday’s assignment (some of which was
done in class, and you can copy that work), plus §11-6 #4 or #5 (your
choice).
|
|
|
Th 3/18/010
|
HW due (optional for Form V): Read §§12-1 and 12-2;
write §11-6 #1, 13. Between now and the end of spring break, I would also
encourage everyone to read this essay by a high
school math teacher in Brooklyn. It is provocative and, in my opinion,
extremely well written.
|
|
|
F 3/19/010
|
HW due: Read §§12-1 and 12-2 if you have not already
done so; memorize the first series in the large box on p. 616, namely the
series for exp(x), plus at least
one of the others.
In class: Quiz (10 pts.) on power series.
Sample question: Evaluate e2.7
by using a power series.
Answer: e2.7 = 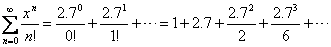
|
|
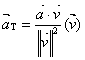
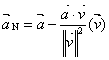

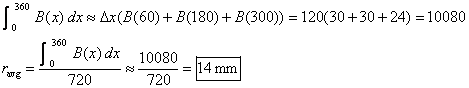
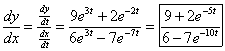 , which has limit 1.5 by inspection as
, which has limit 1.5 by inspection as