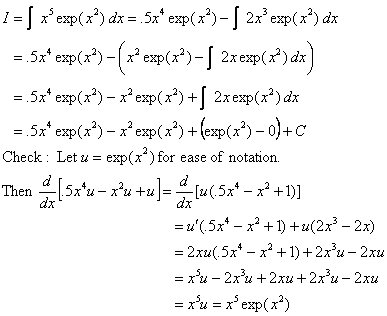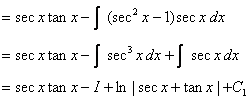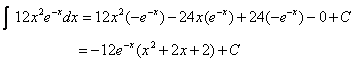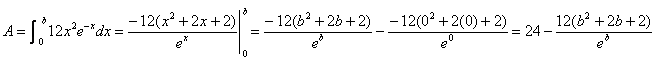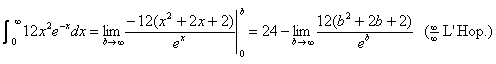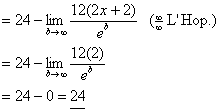|
M 2/1/010
|
HW due: Read §9-2; write §8-8 #19 only (using the
given result of #18 as a lemma), §8-9 #13 (see below), §9-2 any two of your
choice from #1-10. Recall that we covered §9-2 earlier in the year, when we
were doing the product rule.
In §8-9 #13, also calculate the total length of the outline of the “crescent
moon” shape shaded on p. 423.
|
|
|
|
The following anonymous
e-mails were received with date/time stamps of 20100201 2055 and 2158 EST, respectively:
Hi Mr. Hansen, I've got an AP review book, but I'm not sure what the best way
to use it is for Wednesday's test. Do you recommend going through the
sections pertaining to the material that we covered in Chap 8/9, or just
sticking to the miscellaneous questions and practice exams at the end? Thanks
very much
Response: The bulk of the test
will focus on material in Chapters 8 and 9.
Dear Mr. Hansen, I know this is an odd request, but I was wondering if there was
any chance of postponing the HappyCal test scheduled for this Wednesday by 1
day. The reason I ask is because the season premiere of "Lost" is
Tuesday night. It is a 3 hour event ending at 11, and I will be watching it
in its entirety, as will many other students I'm sure. I have followed this
show for 5 years now, and I am not about to miss the premiere of the final
season. I know this idea probably isn't appealing to you, but perhaps we
could poll the class on Tuesday and vote on whether or not to have the test
Thursday. Thank you for considering this. Sincerely, An avid "Lost"
fan
Response: Wednesday is a conflict
with chemistry; Thursday is a conflict with physics. Since more of you are
involved with physics, it seemed reasonable to have the test on Wednesday.
Friday is out, because the format cannot be accommodated in a 40-minute
period. There are always tradeoffs of one type or another. I don’t want to
sound heartless or insensitive, but there is such a thing as a VCR (and, I
hear, some newfangled device called a TiVo). I suppose we could take a quick
vote, but to delay a test for a TV event would be a first for me in my 12
years of teaching at STA.
|
|
|
T 2/2/010
|
Class will meet in MH-311 today.
HW due: Read §9-3; write §9-2 #11, §9-3 #13-23 odd, 29, 31, 42, 44. You may
copy #21 from below if you wish.
21. u dv
x5 exp(x2) [Unworkable as is. Reassociate to make right-hand factor
easier.]
-----------------------------------
.5x4 2x exp(x2) [Now
differentiate on left, antidifferentiate on right.]
2x3 exp(x2)
----------------------------------- [We need to reassociate again to make
right-hand factor easier.]
x2 2x exp(x2)
2x exp(x2)
----------------------------------- [We need to reassociate one last time.]
1 2x exp(x2)
0 exp(x2)
Let I = the unknown integral. Therefore,
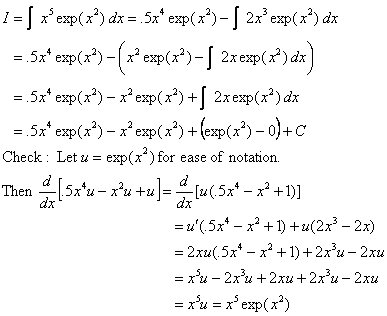
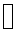
|
|
|
|
OK, everyone, I spoke with
Dr. Labaree and asked about STA policies regarding postponement of tests.
Please note, this is a change from the original announcement. I have sent
e-mail to everyone to confirm. Here is what we are going to do:
1. The test will be on Thursday, period.
2. If our A period is late (or even if, miraculously, it starts on time) on
Wednesday, we will use the time for additional review and Q&A. There will
be no half test or anything complicated like that!
3. If our A period is canceled (as is sometimes the case) or if school is
canceled altogether, we will have the test on Thursday and you can call my
voice mail, 703-599-6624, to get questions answered.
In class on Tuesday, I said I would post a couple of additional solutions for
you to look at from §9-3. Here they are:
29. 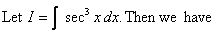
u dv
sec x sec2 x
sec x tan x tan x
so that 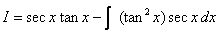
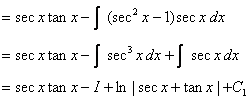
Therefore, 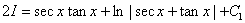 , from which we conclude that I itself equals , from which we conclude that I itself equals
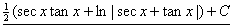 . .
Note:
In this problem, we used the formula from p. 292 for  . .
This is one of the formulas that you are
required to memorize for the entire year.
(And, if you think about it, that is why all of
your tests are cumulative. Even though tomorrow’s
test focuses on Chapters 8 and 9, everything
from earlier in the year is potentially “in play.”)
44. Use rapid repeated integration by parts to evaluate 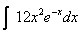 as follows: as follows:
u dv
12x2 e−x
24x −e−x
24 e−x
0 −e−x
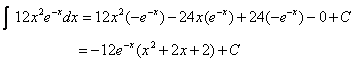
Therefore, we can apply FTC1 to get an equation
for the area A under the function’s
graph between 0 and b:
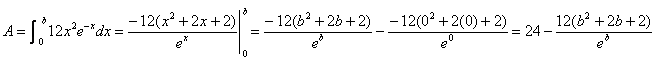
By L’Hôpital’s Rule (also recycled from earlier
in the year!), we get
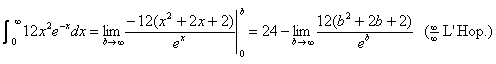
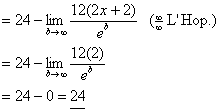
|
|
|
W 2/3/010
|
LOCATION
NOTICE: Class today will be held in MH-001, a.k.a. the “Air Handler Room.”
In class: Pop quiz from an AP review book.
|
|
|
Th 2/4/010
|
LOCATION
NOTICE: Class will be held again today in MH-001, a.k.a. the “Air Handler
Room,” because of NAEP testing in MH-102.
Test (100 pts.) on everything through §9-3, with emphasis on Chapters 8 and
9. The format will be multiple
choice: 12 questions without calculator, then 8 questions with calculator
permitted. You will have a strict 25-minute time limit for each half. Use
your AP review book to prepare for the difficulty level that is expected.
Last Friday’s quiz is a good example. (The mean score was 4.7/12, or 39%,
which is approximately equivalent to a low passing score on the AP.)
To convert AP percentages to STA grades, I generally add 25 to 30 points. The
precise curve I have used in most years is y = .8x + 40, where x = raw AP score as a percentage, y = recorded score. I adjust this
based on my personal judgment of the class and the difficulty of the problems
on the particular test. For example, imagine that on a 20-question test you
answer 14 correctly, you make 4 incorrect guesses, and you omit 2 questions.
Your raw score is 14(4) + 4(−1) + 0 = 52 out of 80 points possible,
which is 65%. Plug 65 into the equation given above, and you obtain a
recorded score of 92 (A). I cannot guarantee that this will be the precise
scoring method, but I have used something close to this for more than a
decade now.
|
|
|
F 2/5/010
|
HW due: Answer all 20 questions from yesterday’s
test, and show some work on your homework paper justifying each answer. Full
writeups are not expected, but you must be prepared to justify your answer.
No guesswork!
Crucial note: There was a typo in #12 that made the problem impossible
to do as posed. To correct the problem (so that the answer matches the answer
given by the publisher!), you need to delete the reference to the first
quadrant. Knowing that the region is bounded by the given curve and the
coordinate axes is sufficient; adding the information about the first
quadrant is not only unnecessary but, in this case, contradictory as well.
For the in-class test that you all took, #12 will be omitted from the
scoring. In other words, the maximum raw score will be 76 instead of 80.
However, I would like everyone to do the corrected version of the question
for HW.
One anonymous e-mail arrived with a suggestion that the scores should be
increased for everyone because of the time wasted trying to answer the
unanswerable question #12. While I am certainly apologetic for the
inconvenience caused by the bad question, I guess I feel comfortable saying
that even if you had wasted 3 minutes on #12, that still left you with 22
minutes for the other 11 questions, which is AP pacing. Making sure that you
do not spend too much time on any one problem is part of what we are
practicing.
|
|
|
M
2/8/010
|
No school because of the Snowpocalypse!
However, there will be an assignment for Tuesday, Wednesday, and Thursday, regardless of whether or not St. Albans is
in session. Be sure to check here each day by 3:00 p.m. for the following
day’s assignment. If time permits, I may post some additional video links or
other resources to help you learn the material without having the benefit of
classroom discussion. If the textbook and other materials prove inadequate,
please see my contact information and call me on
my 24-hour number.
|
|
|
T
2/9/010
|
Old HW
due: People who did not have a perfect
paper last Friday need to re-do all 20 problems on a clean sheet of paper,
showing good work. Joseph needs to do problem 12 only (sorry, I did not
notice that it was marked “omit” on Friday). The other 5 students who had
perfect papers on Friday are exempt from this portion.
New HW due (for everyone): Read
§9-4; write §9-4 #13-18 all, 20. Note that these are application problems. Except for #20, there is no difficult
conceptual work; simply apply the appropriate reduction formulas from the
green box on p. 449. Follow Example 3 on p. 448 for the technique. Note that
after applying the reduction formula once, you will have to apply the
reduction formula additional times on the “reduced” part, as shown in Example
3. Visit wolframalpha.com or calc101.com to perform the “b” part for #13-18.
No password is necessary at calc101.com as long as you are willing to receive
only the answer (no intermediate steps). Wolframalpha.com will show the
intermediate steps if you request them.
For #20, you can type integral(cos^5
x,x) into wolframalpha.com and click the
orange equal sign. Now you see why we do not spend much time teaching this
material nowadays! When anyone with a Web browser can get the antiderivative
faster and more accurately than the best calculus “genius” on earth, there
simply is not much value in developing expertise with algebraic crunching of
this type. You need to know the basic techniques of antidifferentiation, and
you need to be able to apply the formulas, but that is enough. We should
spend the rest of our time focusing on deeper conceptual understanding—in
other words, the hardest and most interesting aspects of the subject.
Note: These assignments are due
Tuesday and will be scanned when we return to school, regardless of whenever
that might be.
|
|
|
W
2/10/010
|
HW due:
Read §9-5; memorize the box at the bottom of p. 452 if you have not already
done so; write §9-5 #3-30 mo3, 35, 36.
Note: This assignment is due Wednesday
and will be scanned when we return to school, regardless of whenever that
might be.
|
|
|
Th
2/11/010
|
HW due:
Read §9-6, this
web page, and §9-7; write §9-7 #3, 9, 11, 12, (13), (15), 19. You may omit
#13 and #15 if you wish, since problems like those are never represented on
the AP exam. However, I recommend that you do them for your own knowledge and
enlightenment if possible. Problem #19 is one that you definitely need to
look at, since it is an example of logistic
growth, which is an AP topic. You may recall that we saw a simpler
example of this about a week ago, on the first question of the “killer” pop
quiz.
We will delay doing any problems in §9-6 until further notice. You may recall
that we already did one integral of that type, in the (a) part of the extra
problem that was due on 1/25. Part (b) was fairly easy, but the lemma in part
(a) required a trigonometric substitution or a table of integrals. We did the
work in class, and that work should be in your notes.
Note: This assignment is due Thursday
and will be scanned when we return to school, regardless of whenever that
might be.
|
|
|
F
2/12/010
|
No school (teacher work
day).
|
|
|
M
2/15/010
|
No school (holiday).
|
|
|
T
2/16/010
|
Normal school day. The
three assignments from last week are due today.
|
|
|
W 2/17/010
|
HW due: Attempt the problem posed in class
yesterday, 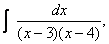
using the method of trigonometric substitution. Compare your answer with what
we obtained.
|
|
|
Th 2/18/010
|
HW due: Read §§9-8, 9-9, and 9-10 (note: §9-9 and §9-10 are mostly review
of previously covered material); write §9-11 #78, 80, 90, plus ID of method
for 33-100 all. For the method identifications, write lightly in pencil in your
textbook. Abbreviations (e.g., IBP for integration by parts) are acceptable.
|
|
|
F 2/19/010
|
HW due: Finish all of your identifications at the
end of §9-11 if you have not already done so.
|
|
|
M 2/22/010
|
HW due: Read §§10-1 and 10-2, which are essentially
review of earlier material. For the written portion of your assignment,
reading notes are required (as always), plus your choice of one of the
following:
1. Write §10-2 #6-12 even, 13.
2. If you prefer, you can begin reviewing for Wednesday’s test, in which case
your work would consist of your review notes and the problems (preferably
odd-numbered) that you have worked in order to begin preparing for the test.
|
|
|
T 2/23/010
|
HW due: Do the §10-2 problems (#6-12 even, 13) if
you have not already completed them. Optional review problems: pp. 498-499
#R2, R3, R7abe, R10, plus several multiple-choice problems picked from your
AP review book.
In class: Review.
|
|
|
|
The following anonymous e-mails were received with
timestamps 20100223 1926 EST and 2015 EST:
Q: Dear Mr. Hansen, Should we know
the derivative and integral formula for inverse hyperbolic trig functions?
Thanks
A: I do not expect you to memorize
any of those. You do need to know that the inverse hyperbolic trig function
integrals are found through integration by parts (just as their inverse
trigonometric counterparts are), and you should be able to handle simple ones
involving sinh and cosh if required. If I expected you to know the most basic
fact about the arctanh function (a.k.a. tanh−1 function),
namely that its derivative is (1 − x2)−1,
then I would provide that fact as something you had in front of you while
doing a problem. I wouldn’t tell you that integration by parts was the
technique to use to find the integral of arctanh, but I think you’ll agree
that knowing the derivative of arctanh makes the integration by parts quite
straightforward. Note, also, that the integral of tanh x is a simple u-substitution,
provided you know that tanh x =
(sinh x)/(cosh x), and it would be entirely fair to ask questions of that sort.
Q: Since they are not included on
the AP syllabus, will hyperbolic functions be covered on tomorrow’s test?
Thanks.
A: Yes, but only the simpler ones.
There will definitely be no integrals that require hyperbolic substitution!
However, you need to know the definitions of sinh x and cosh x. You also
need to know that the derivative of sinh x
is cosh x, that the derivative of
cosh x is sinh x, that tanh x is
defined as the ratio of sinh x to
cosh x, and the simple consequences
of those facts. The questions testing knowledge of hyperbolic and inverse
hyperbolic functions will be custom-written, since they are not found in the
standard AP review books.
|
|
|
W 2/24/010
|
Test (100
pts.) through §10-2. Location: MH-001 (“Air Handler Room”). Format will be identical to the format of the Feb. 4
test. I need to be there early, at about 7:35, for a student who needs to
begin the test early.
|
|
|
|
The following anonymous e-mail was received with
timestamp 20100224 1802 EST:
Q: Mr. Hansen, I have a good deal
of work tonight, and I noticed that the assignment you posted was to write up
each of the problems on todays test. I personally think this to be an unfair
assignment because a) we have not even finished the test, and b) I am
confident that I have all the right answers marked on my sheet, having
corrected all of the ones I got wrong after class. To re-write every problem
seems like busywork to me, because there were no problems that seriously
confused me. I can see how the write up is a good learning exercise, but I
think we should do it the way we did last time: after the test is over, use
that night to get all of the right answers. If we have the correct answer key
the following day, we need not write up each problem over the weekend.
-anonimis
A: It is possible that you and I
have different definitions of the word “unfair.” I use the word to refer to
bias, favoritism, or no-win situations (for example, a situation in which no
matter how much course knowledge the student demonstrates, it is impossible
to earn an A for the quarter). With all due respect, I do not see how any of
those situations apply in this case. Since the requirement was for “a little
bit of work” as opposed to a full writeup, I was hoping to provide an
assignment that my students would be able to complete in about half an hour.
I understand that you find this to be mere busywork, but I think there are
others who will find a strong emotional (and hence learning-related)
connection to problems that they recently grappled with under time pressure.
|
|
|
Th 2/25/010
|
HW due: Write up questions 13-20 from yesterday’s
test. Provide a little bit of work for each one. You should have taken your
question sheet with you when you left.
In class: Finish questions 1-11.
|
|
|
F 2/26/010
|
HW due: Write up questions 1-11. Provide a little
bit of work for each one. You should have taken your question sheet with you
when you left. If you need an extra set of questions (either 1-12 or 13-20),
please ask a classmate. I will also leave a single spare copy in the sorting bin outside my office. Please
use the library copier to copy it if you need to, but then return it to the
bin when you have finished.
|
|