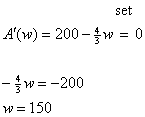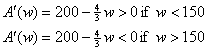|
M 1/4/010
|
Classes resume. No additional written HW is due, but
I strongly recommend that you study for your midterm exam for at least a few
days during the break. To help you, I am posting blank copies of all previous
tests, as well as a practice midterm exam. Note: Be sure to do your studying first, since the practice exam
does not cover every single topic that you are required to know on the real
midterm exam. In other words, you cannot treat the practice exam as if it
were a comprehensive diagnostic test. Instead, treat it as a “confidence
check” to test yourself after you have prepared and studied.
The midterm exam covers all material discussed in class (including famous
mathematicians Newton, Euler, Gödel, Weierstrass, Mandelbrot, Koch, Leibniz,
and Cantor), the calculus of logic, proof of the equivalence of FTC1 and
FTC2, proof of CRI, proof of the change-of-base formula, proof and application
of the derivative of an inverse, and all material in the textbook through
§8-4 except for §8-3. (We will do §8-3 in the second semester.)
The statements of the following theorems should be completely solid, both the
hypotheses and the conclusions: FTC1, FTC2, IVT, EVT, MVT. All can be found
on the BC Calculus Cram Sheet.
|
|
|
T 1/5/010
|
HW due: Read §8-2 and the green box on p. 368; write
§8-2 #13-19 all, 21, 22.
|
|
|
W 1/6/010
|
HW due: Read §8-4 (note: we are skipping §8-3 for
the moment); write §8-2 #20, 23, 24, 39, §8-4 #9, 11, 14.
|
|
|
Th 1/7/010
|
Review. NOTE:
CLASS THURSDAY AND FRIDAY WILL MEET IN THE “AIR HANDLER ROOM” (MH-001).
In class: Go over Sleep Week Test, prove (via dy slicing) that the area of any triangle equals bh/2.
|
|
|
F 1/8/010
|
Review. NOTE:
CLASS THURSDAY AND FRIDAY WILL MEET IN THE “AIR HANDLER ROOM” (MH-001).
The following anonymous question was submitted with date/time stamp 20100107
2048 EST:
Mr. Hansen, On the homework website, you said that we are responsible for
"all material discussed in class (including famous mathematicians
Newton, Euler, Gödel, Weierstrass, Mandelbrot, Koch, Leibniz, and Cantor),
the calculus of logic, the proofs of the equivalence of FTC1 and FTC2, the
CRI, the change-of-base formula, the derivative of an inverse, and all
material in the textbook through §8-4 except for §8-3." My question: can
proofs in the book that you didn't list above (even/odd derivatives, MVT,
etc.) be on the test? Thanks
Answer: No, I am specifically
excluding other standard proofs (such as even/odd derivatives) so that you
can focus your studying better. There may be one or two proofs on things
never covered in the textbook, but they would be relatively short and
straightforward. An example, taken from yesterday’s class, would be to prove
that there is a solution to the diff. eq. dy/dx = y − 2x that has
no curvature. That is a “proof” in the sense that you have to show,
rigorously, that it is possible to find a solution track for y such that the second derivative is 0
everywhere along that track, but it is not something you would memorize for
“regurgitation” purposes. The only standard proofs I am expecting you to
reproduce on command for the midterm are the equivalence of FTC1 and FTC2,
CRI, change-of-base formula, and derivative of an inverse. There will be no
proof of MVT, no proof of FTC itself, and not even the relatively easy proof
that PR + CR lets you prove QR.
Note that I may ask you to prove De Morgan’s Laws, but if so, I would state
them for you (you don’t have to memorize them in advance), and then all you
would have to do is construct a truth table proof using your knowledge of the
calculus of logic. Also, I might ask you to derive something like the formula
for the antiderivative of the cotangent function, but as you recall, that is
really nothing more than a “u
substitution” (let u = sin x, du
= cos x dx). Finally, since nearly any geometric formula can be derived
by using the calculus, I may ask you to do something akin to the two we have
already seen in class: Aparabolic
arch = bh/3, Atriangle = bh/2.
|
|
|
M 1/11/010
|
Mr. Hansen will be on campus beginning at
approximately 1:45 p.m. If you have any questions to answer in person, this
would be a good time to do it.
The following anonymous e-mail was submitted with date/time stamp 20100110
1305 EST:
Dear Mr. Hansen, I have been studying the listed proofs for the upcoming
midterm, and I found that it might be useful to practice a few more geometry
proofs other than the parabolic arch and triangle area proofs. I'm not sure
if you will even put other geometry proofs on the exam, but I am interested in
perfecting the technique... Could you possibly recommend a good problem or
two that I can work on? I could probably come up with a few on my own, but I
figure you must know a tricky one or two that I can grapple with. Also, last
night I attempted to find an indefinite integral for the secant and co-secant
functions. I ultimately came up with the answers, but the problems were much
more complicated than integrating tan, cot, sin, or cos. Is this something
that you would put on the exam? Or would the integration problems always work
out nicely as in section 6.3 with "u-substitution"? Instead of
employing the "u-substitution" technique for integrating sec(x)dx,
I multiplied the integrand by cosx/cosx, substituted (1-sin^2x) for the
denominator, factored, used partial fractions to get two separate integrals,
then did a u substitution (as well as a v substitution) for each integral,
and used some tricky algebra to get ln(abs(secx+tanx))+C=the integral of
secxdx. Is this kind of problem something that would be on the exam? My last
question is whether or not we need to know proof by induction. I don't
believe you mentioned it, but I'm not sure whether I should study it
anyway... Thank you so much for your time.
Answers:
1.(a) Prove that if a sinusoidal curve has period P, amplitude A, and
centerline y = 0, then the area
under one arch equals 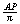 square units. square units.
(b) Prove that the area of an isosceles trapezoid with acute base
angles of 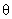 equals equals 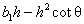 , where b1
denotes the longer base. , where b1
denotes the longer base.
2. Indefinite integrals of secant and cosecant should be memorized. The
proofs require a “trick” (see p. 292) that is hard to remember, and I do not
expect you to remember the trick. Problems involving antiderivatives of
secants and cosecants are fair game (since you were supposed to have
memorized those formulas), but you would not be expected to prove or
re-derive the formulas. The only antiderivatives I intend to ask are those
that are either straightforward from formulas we have memorized (see, for
example, the green boxes on pp. 292-293) or those that are based on u substitution.
3. Your method for  sounds legitimate,
but the more straightforward method is on p. 292. sounds legitimate,
but the more straightforward method is on p. 292.
Again, remember that deriving that formula is not expected, but using it is
certainly something you could be held responsible for.
4. Proof by induction will not be on the exam. It is a precal topic that you
should keep fresh in your mind, since it pops up from time to time throughout
your mathematical education, but there is already plenty of other material
you need to study for the midterm exam.
|
|
|
W 1/13/010
|
The following anonymous
e-mail was submitted with date/time stamp 20100112 2343 EST:
Hi Mr. Hansen. I was had two questions about the upcoming exam. One is what
programs will I need to have on my calculator? So far, I have the Euler
program and the slopefield program, but I don't think I have anything else.
Second, is how much will this exam resemble an actual ap? I took the practice
exam and although the scoring was similar to the a.p. scoring the questions
and format did not look very much like the practice ap exam that I took.
Alright, thanks for your time.
Answers:
0. First of all, please note that “all right” is two words. Thank you (sorry,
once a proofreader, always a proofreader).
1. You need your EULER program for certain. Since I cannot find the bugs in
the SLOPEFLD program, you can rest assured that any slope field plotting you need
to do will be feasible by hand, as on the Dec. 17 test.
2. The midterm exam will not be in AP format. We will do many practice
assessments in AP format later on, including (if time permits) a full-length
practice exam. Format will be similar to the practice exam: a mixture of
short answer and free-response problems. There may also be some
multiple-choice or Always/Sometimes/Never problems. Also, you should be able
to state the following theorems precisely, both the hypotheses and the
conclusions: FTC1, FTC2, IVT, EVT, MVT. All can be found on the BC Calculus Cram Sheet.
_____________________
The following anonymous e-mail was submitted with date/time stamp 20100113
1744 EST:
Dear Mr. Hansen, I'm not understanding how to prove that there is a solution
to the diff. eq. dy/dx = y − 2x that has no curvature. Do you think you
could post at least the gist to this proof/show, or guide me in the right
direction? Thanks very much.
Answer:
No curvature means no concavity. No concavity means second derivative 0
everywhere on the solution track. So, compute the second derivative, set
equal to zero, and see if the curve that you get satisfies the diff. eq. (It
does. In fact, the solution in this case is the line y = 2x + 2, which has
slope 2 everywhere and no concavity. Along that line, y − 2x = 2 by
algebra, and y − 2x is what the original diff. eq. said
should equal dy/dx, which is 2 for this solution.)
_____________________
The following signed e-mail was submitted with date/time stamp 20100113 1756
EST:
Sorry this email is coming to you the day before the exam; I had asked you
earlier to see the answer key for problem 2b on test # 5; do you think you
could post some form of it online? I would ask a classmate, but its a little
difficult to get the the right format for this type of problem orally and
especially over the phone; I think a visual aid might help more.
Answer:
You made it just under the wire! This is the last question I will be able to
answer before the exam, since I will be unavailable for the remainder of
tonight and tomorrow morning. The question was this:
Let g
be any function at all, such that g
is defined on 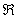 and has a continuous derivative. Write an
expression for g(x) if g(.05) is known to be 2.181 and knowledge of and has a continuous derivative. Write an
expression for g(x) if g(.05) is known to be 2.181 and knowledge of 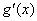 is available. Prove that your answer for g(x)
works, in other words that taking the derivative gives is available. Prove that your answer for g(x)
works, in other words that taking the derivative gives 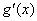 and that g(.05)
= 2.181. and that g(.05)
= 2.181.
Solution (by inspection): 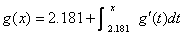
Proof that the solution works:
(1) Take derivative of RHS to get 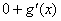 by FTC2, which is
what it needs to be. by FTC2, which is
what it needs to be.
(2) Check value of g(2.05)
by plugging in to RHS: 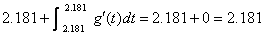 as required. as required.
|
|
|
Th 1/14/010
|
Midterm
Exam, 8:00−10:00 a.m., MH-313.
What to bring: Graphing
calculator, spare batteries, several sharpened pencils, erasers.
What to leave behind or in the hall:
Cell phones, PDAs, iPods, scratch paper, notes, textbooks, food, drinks.
Possession of any of these items in the examination room will be considered
an honor offense.
The exam covers all material discussed in class and everything in the
textbook through §8-4, with the exception of §8-3. See the calendar entries
for 1/4, 1/8, 1/11, and 1/13 for more details, practice tests, and a practice
exam.
|
|
|
M 1/18/010
|
No school (holiday).
|
|
|
T 1/19/010
|
No school (teacher work day).
|
|
|
W 1/20/010
|
Classes resume.
|
|
|
Th 1/21/010
|
HW due: Read §§8-3 and 8-5; write §8-3 #1, 4, 9, 11,
12. Use the optimization framework given in class. The first one is done for you
below as an example, and you should either copy it or compare your solution
and understand any minor differences in presentation that occur. Challenge (optional): Develop a
parameterized solution to #12.
Let l = length (vertical dimension
shown in sketch), in ft.
w
= width (horizontal
" " " " ),
in ft.
Use constraint to reduce 2-vbl. optimiz. problem to a single vbl.
2w + 3l = 600  3l = 600 − 2w 3l = 600 − 2w  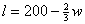
Max. 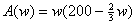
s.t. w
> 0
Find crit. point(s):
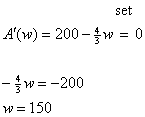
Check endpts. [must always show this step, but here you can write “no endpts.
to check”]
Verify that crit. pt. solution is a max.:
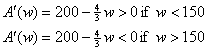
Since 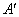 changes sign from
pos. to neg. at changes sign from
pos. to neg. at 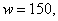 local max. is local max. is 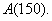
Since there are no other crit. pts. on the domain of A, 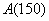 is also the global
max. is also the global
max.
Answers: 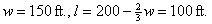
Note: Points are deducted on the AP
if you do not show that you are checking endpoints, and points are deducted
if you find a local max. without justifying that it is a global max. Points
are also deducted if you find an extreme point but do not verify that it is of
the proper type, i.e., max. or min. (The reason for the last rule is that
students who go out into the real world, armed only with a dangerous
knowledge of “take derivative and set equal to zero,” are just as likely to
find the worst possible answers as
they are to find the best possible answers.)
Finally, note that the second derivative test can sometimes speed up the step
of checking whether your local extreme point is a max. or a min. (Not always!
Remember, if the second derivative is 0, you get no information.) In this
problem, 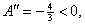 proving that A(150) is a local max. It is not
enough to say proving that A(150) is a local max. It is not
enough to say 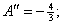 you must say you must say
“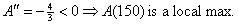 ” The AP graders will not know that you know that the
important issue is checking to see if the second derivative is negative
unless you make it clear. Communication is crucial! ” The AP graders will not know that you know that the
important issue is checking to see if the second derivative is negative
unless you make it clear. Communication is crucial!
|
|
|
F 1/22/010
|
Class will
meet in MH-311 today.
HW due: Make sure you have read §8-5 so that we can discuss it meaningfully. I
realize that many of you have College Night on Thursday night, but please try
to finish up your §8-3 problems as well (§8-3 #1, 4, 9, 11, 12).
|
|
|
M 1/25/010
|
HW due: Read §8-6; write §8-5 #3, 7, 9, 22, and the
following problem.
Prove, using methods of the calculus, that (a) the area of any circle is 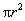 , and (b) the volume of any sphere is , and (b) the volume of any sphere is 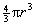 . In part (b), you should use part (a) as a lemma. . In part (b), you should use part (a) as a lemma.
|
|
|
T 1/26/010
|
HW due: Read §8-7. No additional written work is
due. Instead, focus on cleaning up your previously assigned problems.
|
|
|
|
The following anonymous e-mail was received with
date/time stamp of 20100126 2002 EST:
In #3b, I tried solving for x to make a dy equation (dV = pi * x^2 dy), but I
got two values for x and x^2 -----> x^2 = -y-4sqrt(7-y)+11 and x^2 =
-y+4sqrt(7+y) +11. Should I plug both in and solve it twice, or is one of
them a discardable answer (because the x-equation passes into the negative
realm)? Thanks
Answer: Your algebra has some
errors. When you solve for x, you
get
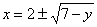 , ,
not the expressions you obtained. I believe you will want to repeat your
algebra steps. (Review the completion of the square.)
Your volume divides into three integrals:
(1) integral for y = 0 to 3 of the
washers with outer radius 4 and inner radius 1;
(2) integral for y = 3 to 6 of the
washers with outer radius 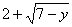 and inner radius 1; and inner radius 1;
(3) integral for y = 6 to 7 of the
washers with outer radius 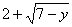 and inner radius and inner radius 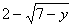 . .
When you add these up, you get the same answer as the (much easier)
cylindrical shells answer given in your book.
|
|
|
W 1/27/010
|
HW due: Write §8-6 #3, 9, 17, and the problem given
below. For #3, 9, and 17, please do each problem using (a) the method of
cylindrical shells and (b) the plane slicing (washer) method. You may omit
one of the (b) parts if time is short.
Required problem: Use radial slicing to develop a general formula for the
volume of a torus (“bagel”). Show your work, and define all of your
parameters clearly.
Optional problem (challenge): Repeat the torus volume problem, using the
method of cylindrical shells. This is harder. (Just set up the integral.
Simplifying requires a table of integrals and is not expected at this point.)
Optional problem (ultra challenge): Repeat the torus volume problem, using
the plane slicing (washer) method. This is much harder.
|
|
|
Th 1/28/010
|
HW due: Write §8-7 #5, 9, 22. Since this is a short written
assignment, please use any additional time to finish both the “a” and “b”
parts for each solid from yesterday’s assignment.
|
|
|
F 1/29/010
|
HW due: Read §8-9 (we are skipping §8-8) and memorize the formulas on p.
418 and p. 420; write §8-9 #1, 2, 3.
|
|