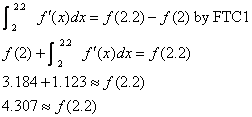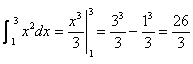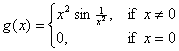|
M 11/2/09
|
No additional HW due.
In class: Vote on policies and points for the second quarter. If you have
specific suggestions for changes, be prepared to propose them in a clear
manner so that they can be discussed.
|
|
|
T 11/3/09
|
Quiz on inverse functions and recent material discussed
in class.
|
|
|
W 11/4/09
|
HW due: Read all of Chapter 4, skipping over the
parts that are redundant and paying special attention to those (such as the
bottom of p. 149) that involve tricky explanations. Then
write §4-5 #21, 22, 23, §4-6 #31-34 all.
In the reading, you may safely skip over things that you are already good at.
For example, most (though not all) of you are good at implicit
differentiation, which means that you may be able to skip reading §4-8.
|
|
|
Th
11/5/09
|
HW due: Read §5-3; write §4-7 #3, 7, 12, §4-8 #12.
|
|
|
F 11/6/09
|
No school (teacher work day).
|
|
|
M 11/9/09
|
HW due: Review problems on pp. 173-175 #R2-R8 all, plus
your choice of problems #T7-T17 on pp. 176-177. (Do as many as time permits.
Please especially try to do #T15-T17.)
|
|
|
T 11/10/09
|
Test (100
pts.), cumulative through Chapter 4.
By your vote, this test will be held in MH-001, where there is room to spread
out. Bring your HW binder for a spot check to occur during the test.
|
|
|
W 11/11/09
|
HW due: Read §5-4; write §5-3 #1-4 all, 6-36 mo3,
37, 38.
|
|
|
Th
11/12/09
|
HW due: Read §5-5; write §5-4 #3-42 mo3, 43, 44, 46,
and the exercise below.
99. In your own words, explain why local linearity (with finite slope) is
equivalent to differentiability at a point.
|
|
|
F 11/13/09
|
HW due: Read §5-6; write §5-5 #4, 7-12 all. You may
wonder what other sort of integral could possibly exist other than the Riemann integral.
Here is one: the Lebesgue integral.
|
|
|
M 11/16/09
|
Announcement:
Class today will be held in MH-001.
HW due: Read §5-7; write §5-6 #1, 1, 3, 4, 5, 6. In other words, do #1 twice
so that you have practice writing out the MVT. Here is one format I can
recommend:
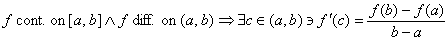
|
|
|
T 11/17/09
|
HW due: Read §5-8 and this handout. You will eventually
be responsible for showing that FTC1 implies FTC2 and conversely. There are no
additional written problems for today, but you must be prepared to give a
reason for each step in the proofs shown in the handout.
|
|
|
W 11/18/09
|
HW due: Read §5-9; write §5-8 #4-9 all. If you
cannot do #4 and #5, then do all the rest. (Note that #6 uses #4 as a lemma.)
|
|
|
Th
11/19/09
|
HW due: Read §5-10; write §5-10 #3, 4, 7. Also
choose any 2 problems from §5-9.
|
|
|
F 11/20/09
|
HW due: Work any two additional problems of your choice
from §5-10. If you would rather sleep, then sleep. (I was a couple of minutes
late in posting the assignment.)
|
|
|
M 11/23/09
|
HW due: Please do all of the following in
preparation for your test on Tuesday. I will not collect them, since the first
one has a solution key and the others are not practical to collect and grade,
but you should do them for your own benefit.
1. Prove that Simpson’s Rule is a weighted average of midpoint and trapezoid
rules, namely (2M + T)/3. Compare your solution against
this student proof from 2002.
2. Work a selection of “R” and “T” problems at the end of Chapter 5.
3. Prepare a list of review questions to ask during the first half of class
today.
4. Prepare a Simpson’s Rule program for your calculator. I will not collect
this (how could I?), but you can use it during tomorrow’s test. A small prize
will be awarded for the best program.
Hint: If the number of intervals in
your Simpson’s Rule program is a constant (say, n = 10), you can pre-populate the list of weights (which we
called L3 last Friday) with 1, 4, 2, 4, 2, 4, 2, 4, 2, 4, 1.
Otherwise, if you let the user specify the value for n, you should include logic to force n to be an even integer. The following line should do the trick
as long as the user specifies n to
be greater than or equal to 1:
int((N+1)/2)*2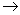 N N
Then, you need to fill list L3 with 1, 4, 2, 4, 2, etc. My
suggestion would be either to
(1) write a loop (you’ll need your calculator manual for this) that puts 4
into all the even-numbered list entries and 2 into all the odd-numbered list
entries, or to
(2) write a clever seq function that returns a 4
for even-numbered entries and 2 for odd-numbered entries, after which you would
STO the result of the seq function into L3.
Regardless of which approach you take, you would then reset L3(1) and L3(N+1) to 1.
In class: Review for test (first half of period), followed by guest speaker, Mr.
Joseph Morris (STA ’62) from MITRE Corporation.
|
|
|
T 11/24/09
|
Test/CFU
through Chapter 5. This test will
be slightly shorter than a typical test so that there is time for feedback at
the end. The score will be recorded for my information but will not play any
role in your quarter average.
|
|
|
|
Thanksgiving break. See answers below.
|
|
|
M 11/30/09
|
HW due: Rework your CFU from
last Tuesday, solving each problem completely. If you have a good solution
to one or more problems (or a solution you think is pretty good), e-mail it
to me. I will post the best ones here on the website. Before you take your
test, you will need to show me that you finished your CFU. It is definitely
to your advantage to do this work, since the test will be quite similar to
the CFU, with additional problems pulled from the “R” and “T” problems at the
end of Chapter 5. Don’t wait until Sunday to start. Work a little on Friday,
a little on Saturday, and you will be in good shape for the test.
In class: Test (100 pts.) through
Chapter 5.
Update: As of 11:00 a.m. on Sunday,
11/29, nobody had sent me anything, except for one anonymous request to post
answers. That is not how it is supposed to work. However, here are the answers
with some of the supporting details.
1. All previously posted online.
2.(a) 4.307
(b) Using 4 intervals, 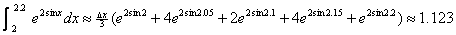 , since , since 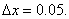 Therefore, 1.123
additional accumulation occurs from x
= 2 to x = 2.2. Answer: 3.184 +
1.123 = 4.307. Therefore, 1.123
additional accumulation occurs from x
= 2 to x = 2.2. Answer: 3.184 +
1.123 = 4.307.
(c)  , provided , provided 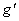 is Riemann integrable. is Riemann integrable.
[Note: It is also acceptable to use x
for the dummy variable here.]
3. Total difficulty = 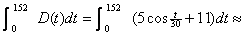 1531.315 difficulty units 1531.315 difficulty units
4. Done in class: If y = exp(x2), then 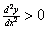 on the positive reals [work must be provided], meaning that concavity is
positive, meaning that the slope is increasing, meaning that there is upward
curvature. Make a sketch showing how the upward-curving graph of the
integrand always leaves some unused area beneath the bounding trapezoid, for
each subinterval. For full credit, the fact that the integrand is positive
should also be mentioned. You can stop there, assuming you explain your
sketch coherently. A rigorous proof was not requested. on the positive reals [work must be provided], meaning that concavity is
positive, meaning that the slope is increasing, meaning that there is upward
curvature. Make a sketch showing how the upward-curving graph of the
integrand always leaves some unused area beneath the bounding trapezoid, for
each subinterval. For full credit, the fact that the integrand is positive
should also be mentioned. You can stop there, assuming you explain your
sketch coherently. A rigorous proof was not requested.
5. Done in class: 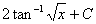
Note to Anonymous: You did not
state what part of question 2 was confusing you. I will try to provide more
explanation here. If this helps (or if it doesn’t), please let me know so that
I’m not stabbing in the dark.
2.(a) This is a differential equation with an
initial condition for f. The
general problem type is common on AP multiple-choice tests (and usually
heavily missed by students). Given: The derivative of an unknown function f (x)
is exp(2 sin x),
and f (2) = 3.184. By FTC1, the
integral of the derivative from 2 to 2.2 equals f (2.2) − f (2),
since f is clearly an antiderivative of 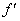 . (We note in passing that since . (We note in passing that since 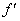 is continuous, an antiderivative, f,
is guaranteed to exist.) Use algebra to write what we know, and then solve
for f (2.2) as follows: is continuous, an antiderivative, f,
is guaranteed to exist.) Use algebra to write what we know, and then solve
for f (2.2) as follows:
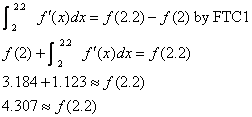
(b) Having solved part (a), you should hopefully find the
work given above for part (b) to be adequate. If not, please send me another
anonymous message.
(c) Repeat the work for part (a), replacing all occurrences
of f with g in the second line. This produces a legitimate expression as
long as 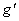 is continuous or at
least integrable (a weaker condition).* is continuous or at
least integrable (a weaker condition).*
Second note to Anonymous: In
#2(a), there is no way that I know of to find the definite integral without
using MATH 9. That is why you were allowed to use your calculator on this
CFU. Please be aware, most of the integrals you will see in your life are
like this: impossible to compute using a “closed form” and FTC1. It is only
in calculus class where many of the problems have a cookbook feel to them:
e.g., 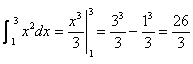 . Real life is rarely so clean. . Real life is rarely so clean.
*Follow-up note regarding #2(c):
It is possible to construct pathological functions that are differentiable
but not integrable. Such a thing
seems impossible at first glance—but remember the Weierstrass
function, which also seemed impossible at first glance. (That was a function
that was continuous everywhere but differentiable nowhere.)
The FTC says that every continuous function has an antiderivative,
and that the definite integral of any continuous function equals the
difference of antiderivatives evaluated at the
upper and lower endpoints. Fine. However, the FTC makes no converse claim
that every function g that is an antiderivative of 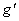 serves as an
accumulator function (in the sense of being able to compute the integral of serves as an
accumulator function (in the sense of being able to compute the integral of 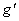 ). Why not? The reason is that continuity of ). Why not? The reason is that continuity of 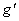 is not guaranteed
simply by the existence of is not guaranteed
simply by the existence of 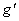 . (Continuity of g
is guaranteed, of course, since . (Continuity of g
is guaranteed, of course, since 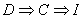 , but that is a different matter.) Consider, for example, the
following bizarre function: , but that is a different matter.) Consider, for example, the
following bizarre function:
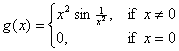
It is an excellent exercise, and probably something that will appear on a
future test, to prove that g is
differentiable on 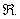 However, However, 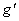 is not Riemann integrable on any interval that passes through 0 or has 0
as an endpoint, a fact that you may be able to prove currently (though I
would not hold you for it just yet). Thus the answer posted above for #2(c)
has now been modified slightly to include the words, “. . . provided is not Riemann integrable on any interval that passes through 0 or has 0
as an endpoint, a fact that you may be able to prove currently (though I
would not hold you for it just yet). Thus the answer posted above for #2(c)
has now been modified slightly to include the words, “. . . provided 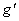 is Riemann integrable.” is Riemann integrable.”
Third note to Anonymous: In #5, I
could provide the work a second time, but the work was already shown on the
board in class. If I provide the work again, am I going to tick off the other
students who took notes? Or am I depriving you of the chance to learn
collaboratively by calling another student? Or am I running the risk of
ticking you off by asking you all these questions? Since I don’t want to lose
you as a happy, involved HappyCal student, I will
quickly re-post the solution:
Let 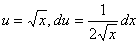 . Then . Then
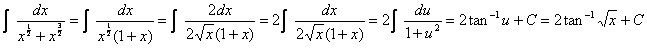
|
|