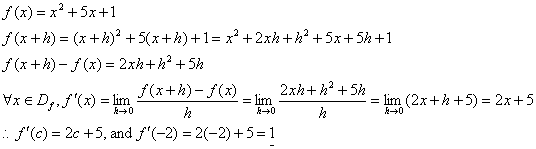Monthly Schedule

(Honors AP Calculus, Period A)

Th 10/1/09	HW due: Read §2-5; prepare §2-4 #1-20 orally, and write §2-4 #21-42 mo3, plus 61 and 70. In class: Time permitting, we will watch the second half of the fractal video.
F 10/2/09	HW due: Read §2-6 and the Wikipedia article on IVT. (Reading notes are required, as always.)
M 10/5/09	HW due: Read this IVT application, §3-2, and the green box on p. 91; write §3-2 #6-12 even, 15. Problem #5 is shown below as an example. Note that you must use the definition of derivative to obtain your answer; there is no credit for using MATH 8 or your knowledge of the mechanical rules of the calculus. For example, everyone beginning calculus student knows that by the “pull the exponent down and multiply” rule. That is not the point. You must apply the limit definition of derivative as illustrated below. 5. Answer: 1
T 10/6/09	HW due: Work with a classmate for this one. Sketch a function g, and try to make it fairly challenging, with sections of both continuity and discontinuity, cusps, asymptotes, etc. Challenge your friend to produce sketches of functions f and h (on comparable sets of axes, not the same axes) such that and . Order your sketches as f, g, h from top to bottom. Then exchange papers and reverse roles!
W 10/7/09	HW due: Selection of review problems on pp. 71-76. Use your own judgment. Confidential to anonymous student #1 last week: Thank you very much, you made my day! Confidential to anonymous student #2 this week: Sorry, since STA knew I was delayed and covered my class Monday, there is no general bonus.
Th 10/8/09	Test (100 pts.) on Chapters 1 and 2, plus all additional material discussed since the beginning of the year. Recent material will be emphasized, but you are still responsible for older material, such as the formal definition of limit, the formal properties of symbolic logic, the set-theoretic foundation of mathematics, what makes a theory scientific, and so on.
F 10/9/09	HW due: Read §3-3, the green box on p. 89, and §3-4; write yesterday’s test to perfection (including the extra question #21). It is permitted to work with classmates and argue with them, as long as you do not copy their work.
M 10/12/09	Columbus Day (no school).
T 10/13/09	HW due: Read §3-5; write §3-3 #3, §3-4 #1-18 all (very quick; no work), #23, #24.
W 10/14/09	HW due: Read green box on p. 105 (presented without proof for now), §3-7; write §3-5 #5, 6, §3-6 #7. Note that #7(a) is done for you below as an example. 7(a) sin 3x = sin(f (x)) = g(f (x)) where f (x) = 3x = “inside” fcn., g(x) = sin x = “outside” fcn.
Th 10/15/09	HW due: Write §3-5 #5, 6; §3-7 #1-22 all. Important: During the day today (Thursday), ask your teachers if you may attend tomorrow’s field trip to the Solar Decathlon exhibit on the Mall.
F 10/16/09	HW due: Fill in the gaps in any previously assigned problems. Field Trip to the Mall (updated schedule): Leave on bus next to Martin Gym at 10:10 a.m. sharp (15 minutes before end of B period). We will take whoever is on the bus at 10:10. We will be gone during all of C period and will return to STA at the start of D period. Your teachers have been asked to excuse you from C period and part of B period if it is possible for you to miss class without disruption.
M 10/19/09	HW due: Read §§3-8 and 3-9; write the problems below. 1. Use mathematical induction to prove that the sum of the first n positive even integers equals n² + n. (Note: There are other ways to prove this, and the easiest is probably to bypass induction completely and use properties of arithmetic series. However, for this exercise, I want you to use mathematical induction.) 2. Given: For nonnegative integers i and n, with . Use mathematical induction to prove the rule of Pascal’s Triangle, viz., that for any positive integer n, and for any positive integer . 3. Differentiate each of the following, and give your answer as an equation in each case. (a) (b) Note:As an anonymous e-mail poster reminded me, this assignment was posted after 3:00 p.m. and also after the 3:55 p.m. deadline I had set for myself following the pep rally and a long student conference on Friday afternoon. I do not normally follow the 3 p.m. rule on weekends, but nevertheless, if you feel that you cannot do this assignment this weekend, I cannot hold you to it. Therefore, all I can do is to ask, politely, if you would do it (since it is a challenging and educational assignment) while keeping in mind that you are within your rights if you choose not to do it. You will, however, need to do the reading at some point, and the problems are representative of problems you will be asked to do later on tests.
T 10/20/09	Read §§3-8 and 3-9 if you have not already done so; write §3-8 #1, 4, §3-9 #1-23 all.
W 10/21/09	HW due: Write review problems on pp. 123-126 #R1, R3d, R5, R7, R8 (assigned by Mr. Kelley) plus #R9.
Online Q & A	Q. I know that many of us are worrying about tomorrow’s test. Most of us had questions that we would have liked to ask you today, but could not get the chance to ask since you were not here the past two days. I don’t know if the test can be moved, but I don’t think that people would do as well as they could do since we have not had review with you the past two days. Just wondering if anything can be done. A. I understand your concern and will adjust the difficulty level of the test accordingly. If you would like, I could post a sample test from a previous year. Any questions you e-mail me tonight will be posted for all to see. Q. When should derivative notation (i.e., dy/dx) be written in cursive? A. Ideally, always, since the d (infinitesimal indicator) travels with the variable it modifies. It is not as if you can separate them. It’s the same with dt, du, dv, etc. However, on the list of possible mistakes, this one is far down on the priority list. If you write dx as separate letters, nobody (not even Mr. Hansen) will deduct points. Q. For the Pascal’s Triangle induction proof, I understand that we do not need to prove anything specifically for i after proving for n. Why is this, and what should we write to denote that the proof applies to i as well? A. The proof Michael gave in class, after editing, was for induction on n, not the more difficult procedure (double induction) that some students may have been thinking of. Since i was given to be in a certain restricted domain, 0 < i < n, and since all of the algebra used in the proof is valid for any value of i subject to that restriction, you really don’t need to say anything. However, it is helpful (and appreciated by most readers) to write that Michael’s first panel constitutes an identity for all legitimate values of i. Q. Could you explain Euler’s Formula? A. There is nothing to explain, and unfortunately we won’t be able to prove it until April. In the meantime, it is a thing of beauty to be admired and pondered, a goal to shoot for. If you are curious, please visit http://www.mathworld.com/EulerFormula.html, where the formula we looked at in class (namely, ) is presented as a special case of a more general result known as Euler’s Formula or Euler’s Identity. Q. Could you explain some important things I missed on [a previous class day]? A. Certainly. Ask your questions, and I’ll keep writing answers as long as I’m awake. Q. There is a question that I wanted to ask you today during class, but you couldn’t make it so I didn’t get a chance. I noticed that we haven’t taken [as many] notes as we have for the past chapters. All I basically have are the ones on induction proofs. But then I remembered how we vaguely went over Euler’s Formula and the functions that were derivatives of themselves. Do we really have to know these for the test or did you go over them just for extra information and further thinking? Also is there anything else other than derivatives, integrals, induction, and stuff from [previous chapters] that we need to know about? A. Euler’s Formula is simply something to know and admire for the moment. The statement of it in the special case for an angle of radians is . Functions that are derivatives of themselves were a thought experiment to lay the foundation for future chapters, not anything to be tested on just yet. I would like you to retain your knowledge of the calculus of logic, the definitions of limit, derivative, and continuity, and the other basic building blocks from earlier chapters, but tomorrow’s test will focus on the more recent material in Chapter 3. Much of the test will stick fairly close to the review problems that Mr. Kelley and I assigned earlier this week. Q. [Multiple questions about induction . . . ] A. The Wikipedia article on mathematical induction is very readable up to subheading 5 (“Variants”) and includes a good, fully worked example. Here is another one: Prove by induction that every positive integer power of 5 ends with a digit of 5. Basis case (n = 1): Clearly, 5¹ = 5, which ends with a 5. Induction step (we must show that if 5ⁿ ends with a 5, then 5ⁿ^{+ 1} must also end with a 5). Since 5ⁿ^{+ 1} = 5(5ⁿ) = the product of 5 and some integer ending in 5 (by hypothesis), the least significant partial product in the multiplication expansion is 25. The 2 (in the tens’ place) may have something else added to it, but the 5 stands alone, since there is no other partial product that involves any positive result smaller than 10. (Q.E.D.) Q. [Multiple requests for a practice test to be posted . . . ] A. OK, here’s one. And if you promise to try the problems before peeking, I’ll let you see the solution key also. Q. What do we need to know regarding the Squeeze Theorem? For example, are we expected to know how to use it in a proof? A. Eventually, yes. For Thursday’s test, no. Q. I am still confused as to where to place the parentheses in chain rule problems. For example, the other day you told us to differentiate y=4t+cos(4t^2+sin(sin(sin4t^2))), and you corrected one of the answers due to incorrect parentheses, stating that y'=4-sin[4t^2+sin(sin(sin4t^2))] * [8t+cos(sin(sin4t^2)) * (cos(sin4t^2)) * (cos4t^2) * 8t]. Why shouldn't the first set of brackets start at the "4- ..." part? A. The original function, y, has a first term of 4t, and the derivative of that first term is 4 with no need for the chain rule. It is the second term that has all of the difficulties. If it helps you, treat each term as a separate problem, and combine terms at the end. The derivative of a sum equals the sum of the derivatives. (Note: You cannot apply a similar rule for products or quotients of functions.) Q. I saw on the practice test you posted online that you gave out bonus points for spare batteries. Is this a policy for this year also, or is it something that has been dropped? A. I guess it can be reinstated! If tomorrow’s test requires a calculator, then there will be a 1-point bonus for having a spare set of batteries. Q. Do we need to know the proof of the derivative of the sine function for tomorrow? A. No, only the result. By the way, always learn your derivative formulas in the “Chain Rule Ready” format. For example, Q. On the practice test there are some symbols that I don’t think we’ve seen before . . . A. Blame this mess on Bill Gates. (Seriously.) It’s a Microsoft browser incompatibility issue. Some of my older files still need to be cleaned up. I think it should be all right now, at least for the October 2006 practice test. Q. What does “exp(x)” mean? A. Standard exponential function of x, i.e., e^x. Q. What is an “accumulator function”? A. A function defined as a definite integral with a variable (usually x) as the upper limit of integration. The 2006 class was given more background and thus should have been able to answer the two questions on the test that referred to this topic. For you, the questions would be harder, but you can still puzzle them out through a process of elimination and comparing clues from elsewhere on the test. Q. What is EVT? A. Extreme Value Theorem. Normally we have covered EVT by this point in the course, but this year is different. The EVT answer choices are there only as distractors.
Th 10/22/09	ANNOUNCEMENT: Test will be held in MH-311, not in either of our other rooms. Please spread the word to your classmates. Test #3 (100 pts.), cumulative on Chapters 1-3 and all material since the beginning of the year except for the names of mathematicians Koch, Cantor, Gödel, and Weierstrass, which will not reappear until midterm. You need to remember Newton, Leibniz, and Mandelbrot for the whole class, however.
F 10/23/09	HW due: Sleeeeeeeep (as announced at the end of the yesterday’s test).
M 10/26/09	HW due: Read §§4-2 and 4-3; write §4-2 #1-29, as many as you feel are necessary to get the hang of the technique. Practice is important. Save some enthusiasm for #29, which is the best of the lot.
T 10/27/09	Essay Quest (50 pts.) covering material since the beginning of the year. Level of difficulty will be comparable to the example given in class yesterday. There is really no way to study or prepare for this quiz. Please, get a good night’s sleep and come to class with your thinking cap on!
W 10/28/09	Quiz (10 pts.) on QR, as announced in class. Sample problem: If , find Answer: . Note to anonymous questioner who asked about the existence of a generalized QR for 3 or more parts: There is no need for such a generalization, since we already have the generalization of PR.
Th 10/29/09	Quiz (10 pts.) on derivatives of trigonometric functions, as announced in class.
F 10/30/09	No additional HW due. A quiz (10 pts.) on implicit differentiation is likely. To practice, you can work a few of the problems in §4-8 (#1-22 all) and use the back of the book or www.wolframalpha.com to check your answers.

Return to the HappyCal Zone

Return to Mr. Hansen’s home page

Return to Mathematics Department home page

Return to St. Albans home page

Last updated: 03 Nov 2009