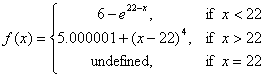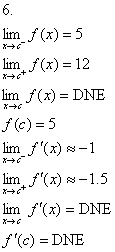|
W 9/9/09
|
First day of class. Discussion of Mr. Hansen’s three rules, fire drill quizzes, what
“mathematics” is, and the beginnings of what a scientific theory is.
|
|
|
Th 9/10/09
|
HW due: Send me a signed e-mail message from the address that you check most
frequently, read §1-1 (pp. 3-4) of your textbook, and visit http://www.StudyOfPatterns.com/videos
to watch topics 3C and 4.
Beginning next Monday, the following equipment is required every day: (1)
textbook, (2) graphing calculator, TI-83 or TI-84 family, (3) 3-ring binder,
and (4) pencil. Sorry, but a spiral-bound notebook or a notebook with folders
does not meet the third requirement.
|
|
|
F 9/11/09
|
HW due: Read §1-2 and prepare #Q1-Q10 (p. 10) and
#1-10 (p. 11) for oral presentation to the class. Reading notes (normally
required) are optional for today. Then, prepare the following written
problems to hand in, using the HW guidelines:
§1-2 #15, 18, 20. You may use the book’s answer for #15 as a guide, although
more writing is required. Show your work clearly, and circle or box your
answers. Use 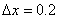 for all three
problems, not 0.01 as used by the graduate student who solved #15. In other
words, your x values for #15 should
be 2.8 and 3.2, for #18 they should be −3.2 and −2.8, and for #20 they should be −2.2 and −1.8. for all three
problems, not 0.01 as used by the graduate student who solved #15. In other
words, your x values for #15 should
be 2.8 and 3.2, for #18 they should be −3.2 and −2.8, and for #20 they should be −2.2 and −1.8.
29. Then, for the example function we discussed in class,  , use your calculator to find a positive value , use your calculator to find a positive value 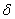 such that for any x in the punctured interval such that for any x in the punctured interval
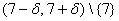
we have 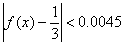 . Write your answer and a short justification of your
reasoning process. . Write your answer and a short justification of your
reasoning process.
Notation: In a situation such as
this, we say that 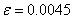 , and we use the lower case Greek letter delta, , and we use the lower case Greek letter delta, 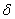 , to represent the radius of the punctured neighborhood. The
backslash character, \, indicates set subtraction. In other words, when we
write , to represent the radius of the punctured neighborhood. The
backslash character, \, indicates set subtraction. In other words, when we
write 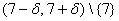 , we mean the interval , we mean the interval 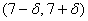 excluding the number
7. excluding the number
7.
Important: I still need e-mails
from Joseph and Tommy. Please see my contact
information for the address.
|
|
|
M 9/14/09
|
HW due: Read §1-3; write §1-3 #2abcd, 6. Problems 2c
and 2d are given below.
2(c). Use your calculator’s MATH 9 feature to answer the question posed in 2(a).
How close did you come?
2(d). Use your calculator’s MATH 9 feature to answer the question posed in
2(b). How close did you come?
The syntax for MATH 9 is found in your calculator manual. In case you have
lost your manual, the syntax is as follows:
fnInt(function,X,A,B)
where X is the variable of integration (normally X), A is the lower limit of
integration, and B is the upper limit of integration. For example, the answer
to #1(a) could be found by fnInt(−.1X^2+7,X,0,5) ENTER.
Warning: MATH 9 (i.e., fnInt) is
calculator notation. As such, it is never allowed to appear in your written
work. AP graders will deduct points if you use calculator notation in your
writeups, and so will I (after a warning period in the fall).
|
|
|
T 9/15/09
|
HW due (abbreviated since yesterday’s class was cut
short by the fire drill): First, make sure that you can produce the formal
definition of “limit” from memory. Second, prove rigorously that 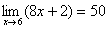 . For this, you cannot use specific values of . For this, you cannot use specific values of 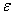 and and 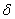 as we did last week.
Instead, you must keep them as variables and show that regardless of the
value of as we did last week.
Instead, you must keep them as variables and show that regardless of the
value of 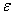 , as long as , as long as 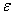 is positive, you can
find a punctured is positive, you can
find a punctured 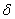 neighborhood of 6
that satisfies the definition’s claim. Hint: Because the “epsilon
band” about 50 is variable, your punctured neighborhood must also be
specified in terms of a variable. You are allowed to use the fact that the
slope of a straight line is constant. neighborhood of 6
that satisfies the definition’s claim. Hint: Because the “epsilon
band” about 50 is variable, your punctured neighborhood must also be
specified in terms of a variable. You are allowed to use the fact that the
slope of a straight line is constant.
|
|
|
W 9/16/09
|
HW due:
1. Watch the Hippasus video (topic #6 at www.StudyOfPatterns.com/videos)
and try to understand each step of the proofs. Although the video is pitched
at a freshman level, you may wish to watch some portions more than once so
that you can really understand everything that is presented. The proofs as
shown on the slides are presented rigorously, though some of the handwritten
explanatory markups are less than rigorous. The goal is that you become
exposed to, and eventually familiar with, the techniques of rigorous
mathematical proof. Although the proof of the main result is a proof by
contradiction, I did not use the term “bwoc” in the video because I was
trying to minimize the number of new expressions thrown at the freshmen.
2. Prove, rigorously, that if a is
a number in the interval [5, 5.000001], then a cannot possibly equal 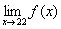 , ,
where function f is the piecewise function
given below. (In fact, the limit is DNE, but you do not need to prove that
just yet.) You may find it helpful to consider three cases: (1) a = 5, (b) a = 5.000001, (c) a 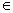 (5, 5.000001). You
may also treat as common knowledge the fact that e to any positive power is a number greater than 1, as well as
the fact that a positive power of any positive number is positive. (5, 5.000001). You
may also treat as common knowledge the fact that e to any positive power is a number greater than 1, as well as
the fact that a positive power of any positive number is positive.
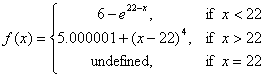
|
|
|
Th 9/17/09
|
HW due: Read §1-4 and the Wikipedia
article on the first-order predicate calculus; write §1-4 #4, 5, 6. For
the Wikipedia article, portions are highly technical. Skim the entire article
(it is highly unreadable in places!), but carefully read §4.6 (“Provable
identities”) and enough of the preceding sections to understand §4.6. If you
are highly motivated, you will discover that Gödel makes an appearance in
§6.1. The only portion I really expect you to understand is §4.6.
|
|
|
F 9/18/09
|
HW due: Recall from class that the 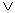 symbol means “or”
(just as symbol means “or”
(just as 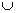 , the union symbol, indicates that we want elements that
are in one set or another set or both). Similarly, the , the union symbol, indicates that we want elements that
are in one set or another set or both). Similarly, the 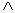 symbol means “and”
(just as symbol means “and”
(just as 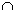 , the intersection symbol, indicates that we want elements
that are in one set and another
set). , the intersection symbol, indicates that we want elements
that are in one set and another
set).
Review the proof given in class that 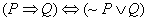 . Using a similar tabular approach, prove each of the
following: . Using a similar tabular approach, prove each of the
following:
1. 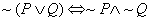
2. 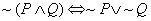
3. 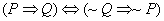
At a certain point, we stop using truth table proofs and instead use the rules
of the first-order predicate calculus when simplifying expressions. For
example, the first-order statement 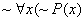 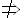 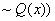 could be simplified
as follows: could be simplified
as follows:
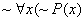 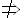 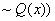 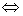 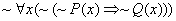 by def. of the by def. of the 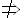 (does not imply) symbol (does not imply) symbol
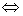 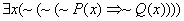 by first identity in
§4.6 of Wikipedia page by first identity in
§4.6 of Wikipedia page
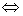 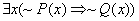 since a double
negative leaves the implication unchanged since a double
negative leaves the implication unchanged
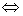 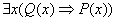 by applying exercise
#3 as a lemma by applying exercise
#3 as a lemma
This is perhaps easier to understand if we let P(x) be the statement “x is pibblish” and Q(x)
be the statement “x is quirglish.”
The original statement says, “It is not the case that for all x, a lack of pibblishness does not imply
a lack of quirglishness.” The simplified (equivalent) statement says, “There
exists at least one x for which
quirglishness implies pibblishness.”
Perhaps you can see that the calculus of logic can be very useful when
untangling complicated legal mumbo-jumbo. Try your hand at each of these,
showing your steps:
4. Simplify 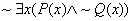 so that your final
answer involves an implication. so that your final
answer involves an implication.
5. Given: 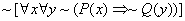
Prove: There exists some ordered
pair (x, y) for which P(x) and Q(y) are not both true.
|
|
|
M 9/21/09
|
HW due: Read §1-5; write #1-10 all. Important: Do all problems for both  and and  , and show left-sided limit, right-sided limit, two-sided limit,
and function value for each. Thus there will be 8 answers for each numbered
problem. You are encouraged to put these in a grid to reduce writing. No work
is required, and for today’s assignment only, you may omit copying the
diagrams in order to save time. You will have to “guesstimate” some of the
tangent slopes. Problem #6 has been done for you as an example. , and show left-sided limit, right-sided limit, two-sided limit,
and function value for each. Thus there will be 8 answers for each numbered
problem. You are encouraged to put these in a grid to reduce writing. No work
is required, and for today’s assignment only, you may omit copying the
diagrams in order to save time. You will have to “guesstimate” some of the
tangent slopes. Problem #6 has been done for you as an example.
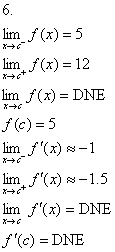
HW due (optional): View topics 1-5 at www.StudyOfPatterns.com/videos
and write a short review/critique of some of them. If you feel comfortable
sharing these with me, please bring them to class. If you like any of the
videos, please tell someone on the staff of The Independent or The
Saint Albans News. In case you didn’t already know, I think videos are
the future of math instruction.
If you wish to remain anonymous, you can proceed as follows.
1. Click here.
2. Then click on my name.
3. When the e-mail window pops up, enter my
name and e-mail as the sender.
4. Click “Send Email” to send the message. It will appear to be coming from
me, and unless you type your name in the body of the message, I will have no
way of knowing who sent it.
By the way, please feel free to use this technique whenever you feel a need
to communicate some class-related feedback and prefer not to speak to me
directly.
|
|
|
T 9/22/09
|
HW due: Read §1-7; write §1-5 #15, 16, 19, and as
many of the review problems R1-R6 (pp. 33-35) as you have time for.
|
|
|
W 9/23/09
|
HW due: Finish writing R1-R6 on pp. 33-35; write
T1-T7 in order to prepare for your test. You should also review your class
notes for the additional material on limits, the calculus of logic, and the
meanings of various terms and symbols: “a calculus,” “the calculus,”
“mathematics,” “wlog,” “bwoc,” “incompleteness,” and the like.
|
|
|
Th 9/24/09
|
Test (100
pts.) on all material covered thus far. Important: Bring your
binder to class so that I can conduct a HW spot check while you are working
on your test.
Last year’s test is available to
give you an idea of what my tests are like. If somebody would like to send me
an answer key, I will correct it and post the answers for everybody’s
benefit. The material emphasized last year was slightly different (for
example, we have not yet discussed chaos this year), but you should be able
to do nearly all of the questions.
|
|
|
F 9/25/09
|
Centennial day of community service (no class).
Arrive at school between 7:30 and 7:45 a.m. carrying a water bottle with your
name on it. Lunch will be furnished.
|
|
|
M 9/28/09
|
HW due: Read §§2-2, 2-3, and 2-4; write §2-2 #1-12
selected as described below.
Count the number of letters in your last name. If the answer is a multiple of
3, then write problems 1, 3, 5, 8, 10, and 12. Otherwise, write problems 2,
4, 6, 7, 9, and 11. This way, all 12 of the problems will be covered, and
everyone has a mix of even- and odd-numbered problems.
|
|
|
T 9/29/09
|
HW due: Write §2-3 #5, 12, 13, 18-21, and try to
answer the Challenge Question.
Challenge Question: We know that it is possible for a continuous function to
have infinitely many places where a derivative fails to exist; if the
troublesome points are cusps, it is easy to imagine infinitely many cusps (at
each integer value of x, perhaps) connected by “smooth” intervals
where the function is
differentiable. However, is it possible for a function to be continuous
everywhere but differentiable nowhere?
|
|
|
W 9/30/09
|
No additional HW due. The Challenge Question from
yesterday is now required, however.
|
|