|
M
5/3/010
|
HW due: Read §§13.3 and
13.4; write §13.2 #14-17 all, §13.3 #1-5 all. The answers to the §13.2
problems are available at hwstore.org, but
please try to do them first without
looking. (You will learn more that way.)
|
|
|
T
5/4/010
|
No additional HW due (Web
access down).
|
|
|
W
5/5/010
|
Read §13.5; write §13.3 #5,
14. Try to do each problem without peeking at the hints below, but if you are
stuck, I expect you to use the hints.
Hints for #5: Find an equation of
each line, using the point-slope technique. Act as if you are playing Green
Globs. Then use your Algebra I skills to find the solution set. Remember to
give your answer in the format {(__, __)} where the blanks are filled in with
the proper coordinates. Check your
solution in both equations, and sketch the system and solution for a
reasonableness check.
Hints for #14:
(1) Find the slope of the line from B to C.
(2) You know that the altitude’s slope is the opposite reciprocal of hint #1.
(3) You know that the altitude must pass through point A, so use the
point-slope technique (Green Globs) to get the equation of the altitude.
(4) Find the equation of the line from B to C (point-slope again).
(5) Use Algebra I skills to find the intersection of hint #3 with hint #4.
(6) Use the distance formula on the answer from hint #5, connecting with the
point A = (5, -1).
Make a large-size sketch of
everything. Graph paper is suggested but not required. If you give up without
trying, that would be a very bad thing.
|
|
|
Th
5/6/010
|
Write §13.4 #5cd, 7a. You
are exempt from this assignment if you helped me move the furniture out of
the Trapier Theater on Wednesday afternoon.
|
|
|
F
5/7/010
|
HW due: Read §13.6; write
§13.4 #2, 3, 5ef; §13.5 #1, 2, 9.
|
|
|
M
5/10/010
|
Multi-part HW due:
1. Read §14.1.
2. Write a definition of the word “circle” that uses the term locus as part of the definition.
3. Write §13.6 #1, 2, 14. In #14de, estimating to the nearest tenth is not
required. Give an exact answer and a ballpark estimate for each.
Hint for #14d: Use distance formula
to calculate AQ, and then subtract the radius of circle Q.
4. Write §13.7 #10. There is an easy way to do this and a hard way. I
recommend that you use the easy way (i.e., not involving slopes, equations, and linear systems).
5. Correct last Friday’s assignment until it is 100% correct. Resources that
you can use to correct last Friday’s assignment include WolframAlpha.com, the answer key on
page 756, and your friends and family.
For example, if you want to check your work for §13.4 #3a, you can visit
WolframAlpha.com. Click the equal sign after typing the following into the
box:
y>=|x+1|
For §13.4 #3bcd, WolframAlpha returns incorrect results, because those
problems are considered too easy to require any assistance by computer.
However, if you are stuck, I will post an answer key for those as well.
For §13.4 #5ef, WolframAlpha requires a slightly more complicated syntax. For
example, here is what you would type in WolframAlpha in order to check your
work for #5e:
plot y>|x-1| and x+3y<12 for x=-10 to 5 for y=-3 to 7
(Needless to say, you can adjust the plotting ranges for x and y by changing the
above command slightly.)
|
|
|
T
5/11/010
|
HW due: Write §13.7 #1-15
odd, 16; §14.1 #1ab. Note: Part (a) for #14 is to do the locus of
points in a plane, and part (b) for
#14 is to do the locus of points in
3-dimensional space.
Your assignment from last Friday, the one that you were supposed to have
corrected by yesterday, will be collected.
|
|
|
W
5/12/010
|
No additional HW due. However,
since you have a quiz coming up on Friday, you should at a minimum be sure
that all your §13.7 problems are done correctly. Resolve any discrepancies
between your answers and the answers in the back of the book. Resources
available to you include Mr. Hansen, the other teachers in the department, WolframAlpha.com, and KhanAcademy.org. No coasting!
Please watch Salman
Khan’s circle equation video. (It is only 9 minutes long.)
|
|
|
Th
5/13/010
|
HW due: Work review
problems on pp. 644-647 #4, 7, 8, 9, 17, 19, 21-25. Also, be sure to watch Mr. Khan’s
9-minute circle equation video if you have not already done so, and then
check out Mr. Hansen’s latest circle
equation video!
Optional HW: This handout on 3-D
plotting may be helpful to you. Remember, 3-D plotting is part of what
you are expected to be able to do for the Big Quiz.
Crew team departs in the afternoon for Stotesbury Regatta. All crew team
members must take the Big Quiz before leaving. Make arrangements with Mr.
Hansen as soon as possible.
In class: Review for first 25 minutes, followed by a practice Big Quiz during
the second 25 minutes. (The practice Big Quiz will count as the real Big Quiz
for crew members.)
|
|
|
|
Here, as promised, are
blank copies and solution keys of both quizzes that you saw on Thursday. I
apologize for the delay in scanning these. I would have scanned them at STA,
which has a fast scanner, but if I had done that, I would have been trapped
in a traffic vortex and might never have made it home.
Practice Version of Big Quiz: Page
1 2 3 4 Solution
Key 1 2 3 4
Stotesbury Version of Big Quiz:
Page 1 2 3 4 Solution
Key 1 2 3 4
|
|
|
F
5/14/010
|
Big Quiz (60 pts.) on Chapter 13. Crew team members will need to take this quiz no
later than Thursday, May 13. Anyone going on the NSA field trip today should take
the quiz after returning to school. Be sure to make arrangements with Mr.
Hansen as soon as possible.
NSA field trip (optional) will
depart at 10:30 sharp from the Martin Gym area and will return by lunchtime.
If you have a conflict on May 25, which is when most of the Form III, IV, and
V students will be going, you may wish to go on the May 14 trip instead. The
May 14 trip is a tour of the museum only. The May 25 trip will include both a
tour of the museum and a hands-on codebreaking workshop conducted by an NSA
mathematician.
Normal STA dress code will be in effect during our time at the museum.
|
|
|
M
5/17/010
|
HW due:
1. Write §14.1 #2, 3ab, 5ab, 6, 8ab, 9. For problems 3, 5, and 8, answer the
question two ways: (a) for the locus of points in a plane, and (b) for the
locus of points in 3-space. Optional: Answer the question (c) for the locus
of points in 4-dimensional or higher space.
2. Watch the locus video. If you
don’t like mine, then please watch this video from YouTube
that has higher production values.
3. (Optional.) Come to JBAM Monday morning at 7:30. Full details and rules
are at jbam.net. I hope to see everyone there!
|
|
|
T
5/18/010
|
Please come to McDonald’s
Week, day 2 (Big Trig competition).
HW due: Watch the locus video if you
have not already done so; read §14.2; write §14.2 #1-5 all. You may copy my
work for #1c from below if you wish.
1.( c) y = 5 gives a line; x2 + y2 = r2
gives a circle if r > 0
Loci can intersect to form a single point, two points, or null set.

|
|
|
W
5/19/010
|
HW due: Redo #1-5 from
yesterday, following the format of the example problem #1c. I am also working
on a new video for compound locus, but because of technical problems on
Tuesday night, the video will probably not be ready until sometime Wednesday.
Let me be very clear about what you need to write for each problem:
- The
setup,
namely a summary of what each of the loci would be. In the example
problem, I identified the first locus as a line and the second as a circle.
Feel free to use identifiers such as “Locus #1” and “Locus #2” as a way
of referring to them. For example, I could have said this:
Locus #1: the line y = 5
Locus #2: the circle x2
+ y2 = r2, r > 0
- A
labeling of cases. Do you
see how I identified the cases as Case I, Case II, and Case III?
- A
quick verbal description of the cases. In the example problem, I wrote a single
point, two points, or null set. Your book’s answer key stops at this
point, as if the verbal description would be obvious. Sometimes it is,
but usually not.
- A
rough sketch of the cases.
Neatness is not really expected, because some of these situations are
hard to sketch. Always be sure to include this step, since otherwise
your “answers” in the previous step could well be RAWR (right answers,
wrong reason). If you omit the sketches, little or no partial credit is
possible, since without a sketch there is little evidence of your
thought process.
For the harder problems, you will probably want to do the last two steps in
reverse order, since sometimes you have to see the sketch on paper before you
can visualize all the possible ways that the loci could intersect. The order
is up to you.
|
|
|
Th
5/20/010
|
HW due:
1. Read §§14.3 and 14.4; review the rules of ABIC, ALTO, PBCC, MCCG from earlier
in the year. The §14.2 problems may be collected and graded for accuracy in
addition to mere completion, so make sure they are good. This assignment is
shorter than usual so that you can get up early and attend Big Trig at McDonald’s. Good luck!
2. The compound locus video, #9B, is
ready to view. I would like you to watch it, but since it was posted at 10:15
p.m. Wednesday, after many of you had gone to bed, you may postpone it a day
if you wish.
In class: Local Big Trig competition, without any interference from
upperclassmen.
|
|
|
F
5/21/010
|
HW due: Watch the compound locus video, #9B, if you have
not already done so. All the material in videos #9A and #9B can be considered
fair game for next week’s Big Quiz.
In class: Guest speaker, Dr. John
Ziagos from Lawrence Livermore National Laboratory (LLNL), on temporary
assignment to the U.S. Department of Energy. Dr. Ziagos will present his
briefing, suitable for a high school audience, on the subject of energy for
the future.
|
|
|
M
5/24/010
|
Big Quiz (60 pts.) on Chapter 14 (locus, compound locus, and ALTO/ABIC/PBCC/MCCG
facts). Material will be comparable in difficulty to the problems on the two
locus videos (#9A and #9B), problems #1-5 in §14.2, and the
sample problems below. Send e-mail (with two underscore characters at the
beginning of the subject line) if you have any questions.
Sample problem 1. Explain why the locus
of points that are equidistant from the vertices of a triangle is the
circumcenter, and explain how to construct the circumcenter.
Solution: This is a review of PBCC. The full explanation is on video #9B.
Sample problem 2: Explain why the
locus of points that are equidistant from the sides of a triangle is the
incenter, and explain how to construct the incenter.
Solution: If we label the vertices A, B, and C, then the locus of points
equidistant from 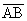 and and 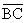 is the angle
bisector of is the angle
bisector of 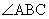 . Similarly, the locus of points equidistant from . Similarly, the locus of points equidistant from 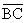 and and 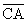 is the angle
bisector of is the angle
bisector of 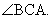 Thus the compound
locus, namely the intersection of the two angle bisectors, is the point (call
it I) that is equidistant from all three sides. Distance from a point to a
line segment is measured as the perpendicular distance, and since (by
postulate) perpendicularity of a radius to a segment occurs iff tangency occurs
at the foot, the three feet constructed from I are radii of an inscribed
circle, and point I is the incenter. Thus the compound
locus, namely the intersection of the two angle bisectors, is the point (call
it I) that is equidistant from all three sides. Distance from a point to a
line segment is measured as the perpendicular distance, and since (by
postulate) perpendicularity of a radius to a segment occurs iff tangency occurs
at the foot, the three feet constructed from I are radii of an inscribed
circle, and point I is the incenter.
[Note: You will not be required to
perform any constructions on the Big Quiz, but you must be able to describe
what is going on. For example, you can write, “Construct the angle bisectors
of 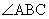 and and 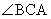 , and label the intersection of the bisectors as I. From I,
drop three perpendiculars, and label the feet as F, G, and H, one on each of
the triangle’s sides. Since I is a compound locus equidistant from all three
sides, we know that IF = IG = IH and that I is the incenter.”] , and label the intersection of the bisectors as I. From I,
drop three perpendiculars, and label the feet as F, G, and H, one on each of
the triangle’s sides. Since I is a compound locus equidistant from all three
sides, we know that IF = IG = IH and that I is the incenter.”]
Sample problem 3: Starting from
point A, construct a segment that divides 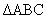 into two triangles
of equal area. Explain why your method is valid. into two triangles
of equal area. Explain why your method is valid.
Solution: Use the
method taught last fall to construct the midpoint, M, of side 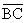 . Since (by MCCG) the triangular region’s centroid (a.k.a.
center of mass) lies on . Since (by MCCG) the triangular region’s centroid (a.k.a.
center of mass) lies on 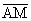 , we know that the areas on each side of , we know that the areas on each side of 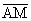 are equal. are equal.
Alternate method: Use the method taught last
fall to construct the midpoint, M, of side 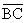 . Extend . Extend 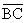 if necessary so that
it is possible to imagine dropping an altitude from A to if necessary so that
it is possible to imagine dropping an altitude from A to 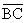 . There is no need to construct the altitude, but note that
the altitude has some length, call it h.
The bases of triangles BMA and CMA are the same, since M is a midpoint. Since
the heights of triangles BMA and CMA are also the same, namely h, and since the area of any triangle
is given by the formula bh/2, the
areas of triangles BMA and CMA are the same. . There is no need to construct the altitude, but note that
the altitude has some length, call it h.
The bases of triangles BMA and CMA are the same, since M is a midpoint. Since
the heights of triangles BMA and CMA are also the same, namely h, and since the area of any triangle
is given by the formula bh/2, the
areas of triangles BMA and CMA are the same.
[Note: Be sure that you understand
both methods. In the alternate version, triangles BMA and CMA have equal
area, but triangles BMA and CMA are not necessarily congruent. The triangles
are congruent only if AB = AC.]
Sample problem 4: Sketch the
orthocenter of (a) an acute triangle, (b) an obtuse triangle, and (c) a right
triangle.
Solutions:
(a) Drop three altitudes, mark the three right angles formed, and label the
place where the three altitudes intersect as O for orthocenter. Note that O
is inside the triangle if the triangle is acute. Most students can do this
without any special practice.
(b) Few students can do this without practice. We did it last fall, and it
was quizzed and tested, but you may have forgotten. Before starting, extend
both sides of the obtuse angle several inches so that it will be possible to
drop perpendiculars from all three vertices. The orthocenter for an obtuse
triangle is always outside the
triangle. If you don’t mind some over-the-top silliness and low production
values, you can watch the new Orthocenter
of Obtuseness video, which shows you exactly how to to find the
orthocenter of an obtuse triangle. The video is 9 minutes long.
(c) Not a challenge, once you know the trick: The orthocenter of a right
triangle is at the right angle’s vertex, since that is where the three
altitudes meet.
Sample problem 5: Explain what is
meant by ALTO/ABIC/PBCC/MCCG.
Answer:
The altitudes of any triangle coincide at the orthocenter. The angle
bisectors of any triangle coincide at the incenter. The perpendicular
bisectors of the sides of any triangle coincide at the circumcenter. The
medians of any triangle coincide at the centroid (a.k.a. center of gravity if
we have a triangle region of uniform density).
Sample problem 6: For points J and
K at fixed positions on circle C, and for arc JK having fixed measure 120,
find the locus of points that are on circle C and equidistant from J and K.
Also explain why 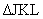 might or might not
have its orthocenter, incenter, circumcenter, and centroid all at C. might or might not
have its orthocenter, incenter, circumcenter, and centroid all at C.
Solution: The locus for L is a compound locus, the intersection of (1) circle
C and (2) the perpendicular bisector of 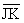 . The compound locus is 2 points, one at the midpoint of
minor arc JK, the other at the midpoint of major arc JK. The first point that
is possible for L produces . The compound locus is 2 points, one at the midpoint of
minor arc JK, the other at the midpoint of major arc JK. The first point that
is possible for L produces 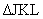 with angle measures
of 120, 30, and 30. Since obtuse triangles have both their orthocenter and
circumcenter outside the triangle, and since the incenter and centroid are
always inside the triangle, it is impossible for all four centers to be at C.
However, the second possibility for point L bisects a major arc of measure
240, thus creating with angle measures
of 120, 30, and 30. Since obtuse triangles have both their orthocenter and
circumcenter outside the triangle, and since the incenter and centroid are
always inside the triangle, it is impossible for all four centers to be at C.
However, the second possibility for point L bisects a major arc of measure
240, thus creating 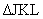 with angle measures
of 60, 60, and 60. Since with angle measures
of 60, 60, and 60. Since 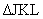 is equiangular, it
is equilateral, and for an equilateral triangle, all four centers occur at C. is equiangular, it
is equilateral, and for an equilateral triangle, all four centers occur at C.
|
|
