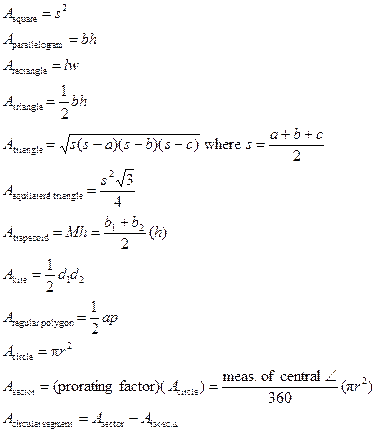|
|
Spring break.
|
|
|
M
4/5/010
|
HW due (F period only): Write §11.4 #2, 4, 7, 10, 11.
Note: This assignment is optional
for E period students, since we already did it orally during E period on
Friday, 3/19.
|
|
|
T 4/6/010
|
HW due: Read §§11.5 and
11.6; write §11.5 #1, 3, 5, 6, 9, and the problem below.
Problem: Without peeking at the
proof of Theorem 106, prove that the area of any equilateral triangle having
sides of length s equals 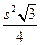 . A diagram and a short bit of algebra are all that will be
expected here. . A diagram and a short bit of algebra are all that will be
expected here.
|
|
|
W
4/7/010
|
HW due: Read §11.7; write
§11.6 #1, 3, 4, 9, 11, and the following problem.
Pentagon
Problem: The Pentagon, where Mr. Hansen worked for about 12 years, is
a large office building whose outer wall forms a regular pentagon having
apothem 634 ft. and side length 921 ft. Compute the “footprint” (area) of the
Pentagon in square feet as well as in acres. Note: This figure will not match the floor space figure published
on various Internet sites, nor will it match the area of the building proper,
since there is a large central courtyard as well as gaps between the five
“rings” that make up the building. Simply calculate the area of the large
regular pentagon.
|
|
|
Th
4/8/010
|
HW due: Read §11.8; write
§11.7 #7, 9, 10, 15, 20.
|
|
|
F
4/9/010
|
HW due: Write §11.8 #1, 2,
4, 6, 10, and refer to yesterday’s
handout in order to prepare for your quiz.
Quiz (10 pts.) will cover the
calculation of the area of a circular segment. You will not have a trig table
available during the quiz. Since I can do the quiz in 2 minutes and 20
seconds, you need to be able to do it in 12 minutes. The time limit will be
strict. Simplification is not required, but you will be required to estimate
your answer (rough estimate only).
To practice for the quiz, you should make up some numbers for the radius and
central angle, then compute the area of the circular segment. Partial credit
is as follows:
2 pts.: sketch showing central angle, radius, and shaded circular segment
2 pts.: formula and partial plug-ins: Asegment = Asector − Atriangle
= 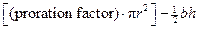
2 pts.: correct expression for Asector
2 pts.: correct expression for both b
and h in the triangle area (using
either trig and Pythag., or trig. and trig.)
1 pt.: correct final expression for triangle area
1 pt.: correct final expression for segment area
Deduct 1 pt. for omitting units, 1 pt. for forgetting to circle final answer.
|
|
|
M
4/12/010
|
HW due: Use a straightedge
to make an “ugly” quadrilateral on a large piece of paper. Make sure that your
quadrilateral has nothing special about it: no parallel sides, no
perpendicular diagonals, and so forth. Then use Hero’s formula twice to compute the area of your ugly
quadrilateral. Show all formulas, plug-ins, and answers. Give answer to the
nearest tenth of a square inch, but round only at the very end of your
problem. (If you round too soon, you will get an inaccurate result.) Measure
your sides and one diagonal as carefully as you can, and use an electronic
calculator or a computer in the final step. Work will be evaluated based on
neatness and completeness.
Bonus (2 pts.): Develop a “wlog” formula for the
area of a circular segment in terms of the radius and the central angle. The
central angle is assumed to be between 0 and 180 degrees. Diagram and work
are required, and you cannot simply copy from a website. Of course, you are
free to use the Internet for inspiration, but on this particular problem, you
may be able to derive the solution more quickly by yourself. All of the top
Google entries, including the Wikipedia entry for “circular segment,” have
difficulties with them: derivation not shown, answer in radians instead of
degrees, overly complicated trigonometric identities used, or some
combination of the above.
Because this assignment is shorter than usual, you should use your extra time
to begin reviewing for Wednesday’s test.
In class: Quiz Redux (10 pts.)
will be the same as last Friday, except with a time limit of 11 minutes
instead of 12. If you have a perfect 10 today (not a 9, not a 9.5, but a
perfect 10), then you can score yourself as a double 10 out of 20. Otherwise,
the score will be whatever you earned Friday, plus whatever you earned today,
all out of 20 points. Warning: Neatness
counts. You cannot earn a perfect 10 if your work is illegible or sloppy.
|
|
|
T
4/13/010
|
HW due: Review problems on
pp. 554-558 #1-37, 39-41. Do as many as you can, focusing on problems that
are of medium difficulty for you. You can skip the ones that you find
ridiculously easy or ridiculously hard. (However, remember that tests always
include at least one hard problem.) The review is for your benefit. Keep a time log.
An answer key is available, but
of course you will need to show diagrams and more work.
Here are some additional angle-arc
review problems to refresh your memory. Do not look at the solutions
(pages 1, 2, and 3) until after you have made a
solid effort. Otherwise, you are simply cheating yourself and wasting time;
you are not really preparing for the test. For review purposes, also try
solving the second puzzle with the chord-chord power theorem, which is much
faster than the method shown in the solution key.
If those were too hard for you, try some easier ones here (with solutions).
Obviously, there are way too many problems, 45 in all, for you to do in a
single evening. Do some over the weekend or on Monday night, and do as many
of the rest as you can on Tuesday night as you prepare for the test.
In addition to grading your homework on a 0-4 scale for completeness, I will
record a qualitative assessment (not part of your grade average) to be used
in the event that a midterm report is needed. For example, if you “bomb”
Wednesday’s test but have excellent review problems, I will write something
like the following to your parents: “Johnny scored a disappointing 56% (F) on
the first test of the fourth quarter. However, because his review problems
showed such thorough preparation and hard work, I am inclined to be generous
in the averaging if he shows improvement later in the quarter.” On the other
hand, if your review problems are of poor quality, I will write something
more like this: “Johnny scored a disappointing 56% (F) on the first test of
the fourth quarter. Because he has demonstrated an unwillingness to spend
adequate time and effort on test review, it will be difficult for him to
climb out of the pit he has dug for himself.”
In class: Review. A pass-fail quiz (0 or 10 points, no in-between) may be
held on the pronunciation of the word “apothem.”
|
|
|
W
4/14/010
|
Multiple HW scan will occur during the test. Bring
your entire 3-ring binder! First
semester assignments (i.e., those before January 20) are exempt, but anything
else is fair game. Recent assignments will be emphasized, but a few older
ones may be spot-checked as well.
Test (100 pts.), cumulative through Chapter 11. There will be no clock
problems, but anything else from the entire year is fair game, including the
angle-arc material (Half SAD, power theorems, etc.) that some people never
fully learned from Chapter 10. Most of the test, however, will focus on
Chapter 11.
Educational fun: Here is the area puzzle we
worked on yesterday. Print it out, cut it apart, and put it back
together! If you get stuck and can’t solve the puzzle, you can use the
cryptic symbols in the middle of each piece to match up against the original
.PDF file.
You will probably want to make a list of area formulas to memorize. Memorization
is an important part of training your brain, but in the interest of kindness,
I will allow you to write any three (3) formulas you wish on a 3" x
5" note card (or a 3" x 5" piece of plain paper) that you may
use during the test. Note that some formulas (e.g., square or rectangle) are
redundant, since there are other formulas that already cover the same
concept. Since every square is a parallelogram, and since every rectangle is
a parallelogram, the bh
formula works for squares and rectangles. Also, the 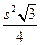 formula for
equilateral triangles need not be memorized, since you can always re-derive
it in a jiffy from your 30°-60°-90° facts, or even (believe it or not) from the formula for
equilateral triangles need not be memorized, since you can always re-derive
it in a jiffy from your 30°-60°-90° facts, or even (believe it or not) from the 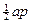 regular polygon
formula. regular polygon
formula.
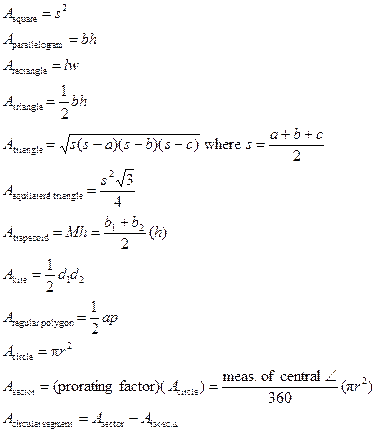
Note: You do not need to memorize Brahmagupta’s formula, nor do you need to list it on your
card. If Brahmagupta’s formula appears on the test
at all, it will be provided for you.
|
|
|
Th
4/15/010
|
HW due: Read §12.1; write
the triangle area puzzle from yesterday’s test.
There are many, many ways to do this problem. Try to do it at least two different
ways so that you can cross-check your work.
|
|
|
F
4/16/010
|
HW due: Read §12.2; write
§12.1 #1, 2, 5.
Bonus puzzle (2 pts.): Find the
area of 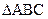 . .

|
Givens for the bonus
puzzle:
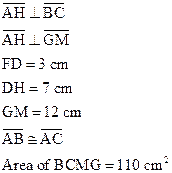
|
|
|
M
4/19/010
|
HW due: Read §12.3; write
§12.2 #3, 4, 7, 8, 11, and be sure to sketch a tetrahedron in #11. (You can
easily find a tetrahedron on the Web, or you can look at #17 on p. 588.)
|
|
|
T
4/20/010
|
Diversity Day (no class).
|
|
|
W
4/21/010
|
HW due: Read §12.4 and the
paragraphs below; prepare for a quiz covering the Fourteen Things to Learn for a
Lifetime handout. Here are some definitions to assist you:
chaos: an extreme sensitivity to
initial conditions; also known as butterfly
effect
For example, it is generally
not possible to predict weather accurately for more than a few days in
advance. The reason is that regardless of how good the measurements of
temperature, humidity, wind speed, and so forth are, and regardless of how
many sensors we plant on land, in the ocean, and in the skies, we will never
be able to account for all the initial conditions that govern how weather
develops. The tiniest perturbation in the initial conditions (including, as
it is said, something as minor as the flapping of a butterfly’s wings) can
create a slight change that, over time, will cause larger and larger changes
from the predicted weather over a larger and larger area, until eventually
the entire world’s weather is different from what had been predicted.
Weather is an example of
chaos. Other examples include fluid
flow, nuclear reactions, traffic flow, people’s lives, and politics.
Consider, for example, how different the world would be if a 6-year-old boy,
Elian Gonzalez, had died off the coast of Florida along with his mother and a
number of other Cubans who were trying to escape from Castro’s government in
1999. Fortunately, Elian survived. (Eleven people died; Elian and two others
survived.) However, since his father back in Cuba wanted Elian returned, and
since the United States was legally required to return him to his father, the
Clinton administration followed the law. This action caused a huge uproar
among the Cuban-American community in southern Florida, who thought that
Elian should stay in America with his great-uncle. In the presidential
election of November 2000, a large number of Cuban-Americans (certainly in
the thousands), still angry over the Elian Gonzalez incident, either stayed
home from the polls or voted for the Republican candidate, George W. Bush. As
a result, Al Gore (STA alumnus, Class of 1965) lost Florida by 537 votes, a
margin of approximately 0.01% (1 part in 10,000). As you may know, the
peculiarities of the Electoral College system in U.S. presidential elections
led that year to a situation where the entire election hinged on the outcome
in Florida. Therefore, the chance event of a young boy’s survival in the
ocean led to a complete change in the election of a U.S. president.
For fun, you can ask
your parents how they met. In most cases, unless they knew each other for a
long time while growing up, their meeting was a chance event that might never
have occurred if the timing had been slightly different. See the movie Back to the Future for an exploration
of this theme.
miracle: an occurrence that passes beyond our
current understanding
causation: the process by which an
effect is produced
Note that this
definition is essentially circular, since there is no way to define effect without referring to causation
in some way. (It is not sufficient to say that an effect is an occurrence
that follows another action, since oftentimes occurrences are random or have
explanations other than the event that preceded them.)
It may surprise you to
know that mathematics, which is useful in so many ways, has nothing to say
about cause and effect. Cause and effect cannot be proved mathematically. To
prove that something causes something else, one has to use the less precise
world of statistics, not math. In statistics, no proof regarding cause and
effect is ever 100% airtight.
solution: a set of mathematical
objects satisfying the conditions of an open sentence, or in the real world,
any set of objects and/or procedures that satisfy a set of requirements
For example, a “data
backup solution” would be a set of hardware, software, and procedures for
ensuring that data are always backed up. A solution to a crossword puzzle is
a set of words that satisfy the requirements of the clues. A Sudoku solution
is a set of numbers that satisfy the rules of Sudoku and include the numbers
originally given in the puzzle.
locus: solution set, though in a
geometric context (since the word locus
is Latin for “place”)
|
|
|
Th
4/22/010
|
HW due: Read §§12.5 and
12.6; write §12.3 #2, 4, 7, 10, and finish §12.2 #11 from the previously assigned
problems. Also note that yesterday’s planned quiz, which was delayed, may
occur today.
Hint
for: §12.2 #11: Part (a) is not hard, since you are given s = 6 for the equilateral faces, and
you can simply multiply the area of one face by 4 to get the TSA. However,
for part (b) you will need to think much harder. A model of a tetrahedron may
help. You may wish to use a dollar bill and fold it as demonstrated in class.
Another thing that may help for #11(b) is to visualize a set of 4 equilateral
triangles out of which a tetrahedron can be constructed. Where is the foot F of the tetrahedron’s altitude? How
far is it from F to a nearby vertex
V of the tetrahedron? (We already
know the distance from V to the
apex of the tetrahedron, namely 6.) You now have enough information to apply
the Pythagorean theorem to find h,
the height of the tetrahedron.
People who found h = 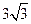 , and quite a few people did that, should realize that
their answer is RAWQ. It is the height of the tetrahedron that we want, not
the height of one of the triangular faces. , and quite a few people did that, should realize that
their answer is RAWQ. It is the height of the tetrahedron that we want, not
the height of one of the triangular faces.
A model that you can cut out to form a tetrahedron:

|
|
|
F
4/23/010
|
HW due: Write §12.4 #2, 3,
12, 18. Also read the following theorem and build your choice of a
tetrahedron model (to assist with §12.2 #11) or a Pac-Man sector model (to
assist with the proof of the theorem).
Theorem: The lateral area of a cone
equals 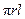 , where r =
radius of cone and l = slant height
of cone. , where r =
radius of cone and l = slant height
of cone.
Proof: Any circular sector region can
be rolled into a cone, and any cone can be formed from a circular sector
region, as can be quickly demonstrated with a model. Wlog,
let x° be the sector’s central
angle, where 0 < x < 360. Let
r denote the cone’s radius, and let
R denote the sector’s radius, which
in general is different from r.
From the model it is easy to see that the lateral area of the cone equals the
sector area, namely 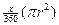 . .
However, since the radius of the sector becomes the cone’s slant height when
the cone is rolled up, we know that R
= l. Moreover, the circumference of
the cone’s base, namely 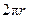 , is the same as the curved arc length of the sector,
namely , is the same as the curved arc length of the sector,
namely 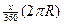 . By algebra, we set . By algebra, we set 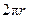 = = 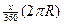 , which simplifies to , which simplifies to 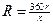 . .
Now, we merely plug the results from above, R = l and 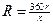 , into the sector area formula from above: , into the sector area formula from above:
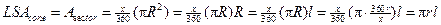 
|
|
|
M
4/26/010
|
Phi Beta Kappa Day (no
school).
|
|
|
T
4/27/010
|
HW due:
1. Write §12.5 #9, 13; §12.6 #8, 11.
2. Put your April homework papers into chronological order. (Some students
like to have the most recent ones on top; others prefer the oldest ones
first. Either way is fine with me.) Some HW papers may be re-scanned, and
correct solutions for problems that have been covered in class will be
required.
3. Begin reviewing for the test. Review problems are pp. 594-597 #1-15 all,
17-21 all. Answers to the odd-numbered problems are in the back of the book,
and most of the even-numbered answers are here. I will not look at your
review problems until Wednesday, but you should at least start working on
them over the weekend.
4. For fun, see if you can identify the formulas listed below. Answer key is here.
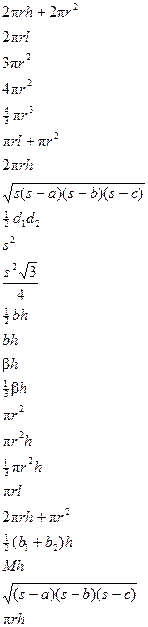
In class: Review.
|
|
|
W
4/28/010
|
Test (100 pts.) through Chapter 12. Area knowledge from Chapter 11 is also fair game
for the test. You need to know all about area in order to compute lateral
surface area and total surface area in Chapter 12, not to mention the
computation of 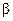 (base area) required
in many volume problems. (base area) required
in many volume problems.
Note card: During the test, you
may use one note card (3 inches by 5 inches) with formula notes. You may put
any 3 formulas that you wish on your card so that you do not have to memorize
all of them. You may write area formulas, volume formulas, or some of each,
as long as the total number of formulas does not exceed 3.
Important: Bring all your review
problems (pp. 594-597) to the test. I will make a notation of how many you
did and to what level of quality. This is not for a grade, but it will be
invaluable to me when I write the mid-quarter comments. Decide which of the
following mid-quarter reports will make your parents happier:
Student
A: “Billy had some trouble with the second test in the fourth quarter.
I think one reason may be that his preparation for the test was woefully
inadequate. He did almost no review problems in the days leading up to the
test. I conclude that either (a) he is satisfied with the low grade he earned
on that test, or (b) he has somehow developed a belief that mathematics can
be learned without practicing. Either way, it is clear to me that he deserved
the low grade he received.”
Student
B: “Although Johnny had some trouble with the second test in the
fourth quarter, I know that he prepared for the test. His review problems
were carefully written, and I could tell that he put hard work and care into
them. He corrected his errors using a different color of writing, and I could
see that he made a good effort to learn from his mistakes. I have every
confidence that his average will improve, because good study habits like
these will always bear fruit in the long run.”
The two fictitious students, Billy and Johnny, each scored exactly the same
score on the test. Whose parents will be more likely to be kind and
understanding when the mid-quarter report comes: Billy’s or Johnny’s?
|
|
|
Th
4/29/010
|
HW due: Read §13.1; write
§13.1 #1-4 all, 19. As always, bring your entire HW binder. Chapter 12 review
problems and some earlier assignments may be scanned.
|
|
|
F
4/30/010
|
HW due: Read §13.2; write
§13.2 #1, 2, 3, 7, 9, 13, and the required additional questions below. If you
have extra time, also do #14-17 all, which are typical test questions.
Required additional questions:
(a) Explain why the slope of a horizontal line is zero. Use your own words,
not something you found in a textbook. It is acceptable to be wrong. However,
your answer must be legible.
(b) Explain why the slope of a vertical line is DNE.
Again, use your own, legible wording.
(c) Explain why Mr. Hansen never uses the term “no slope” when referring to a
vertical line, even though some teachers and textbooks do.
|
|
|
|
|
|