Monthly Schedule

(Geometry, Periods E and F)

M 3/1/010	HW due: Review the Common Tangent Procedure taught in class Friday. When you click on the link, you will see that there are 5 numbered parts. Here is what you are to do for each part: 1. Learn the song. (Or, if you prefer, write a better song!) 2. Read slowly. Read every word, every sentence, following the diagram with your finger. This is not like reading a novel or a newspaper article. This is technical reading. Doing it correctly may take you 10 minutes or more. The diagram would be better if the segment connecting the centers were horizontal, since then the radii, and , would be obviously slanted relative to . 3. Do parts (a), (b), and (c), using the procedure as taught in class. 4. Read slowly. This one is easier than #2. 5. Do parts (a), (b), (c), and (d). If you run out of time, then at least make the starting diagrams. Note: Karl has written a clever Python program that calculates tangent segments lengths. The formula is for an external tangent segment, for an internal tangent segment. However, please do not think that the important thing in all of this is to find “the answer.” If all I wanted you to do was to calculate “the answer,” I would simply teach you the formulas and leave out all the nifty diagrams, and that would be no good. (Geometry without diagrams is like birthday cake without frosting.) In these formulas, circles A and B have radii rA and rB, respectively.
T 3/2/010	HW due: Read §10.5 and the rule of Angle Half SAD; write §10.4 #1, 3, 9, 10, and the problem below. Hint: For #10, let R be the point of tangency between A and B, let S be the point of tangency between B and C, and let T be the point of tangency between C and D. Let x = AR, which makes RB = 20 − x. Then use TTT (Two-Tangent Theorem) to get BS = 20 − x as well. Continue “walking around” in this fashion. Additional problem: (a) Use the “wlog diagram” concept to find a parameterized solution (a.k.a., formula) for the length of a common internal tangent when the circles have radii rA and rB, and d = AB is the distance between their centers. Show your diagrams; do not simply borrow Karl’s formula from the 3/1 calendar entry. (b) What happens if rA + rB = d? (c) What happens if rA + rB > d? (d) Use your parameterized solution from part (a) to answer #14 on p. 465 (no work required).
W 3/3/010	HW due: Listen to the 5-minute radio segment entitled “The Teen Brain: It’s Just Not Grown Up Yet”; make a few reading notes if you have not already done so (it was on NPR’s Morning Edition program on Monday of this week). Then write §10.5 #1-4 all, 18. For #18, please make a huge diagram so that you can see clearly what is going on.
Th 3/4/010	HW due: Read §10.6 and solve the first set of angle-arc puzzles written by students.
F 3/5/010	HW due: Read §10.7; write §10.6 #2, 5, 7, 8, 9, 13. For #8, write A, S, or N (always, sometimes, never) instead of “must,” “could,” or “cannot.” You are also expected to finish yesterday’s puzzles, especially #5, if you have not already done so.
M 3/8/010	HW due: Read §10.8; write §10.7 #11 (justifying all steps in writing), 17, 19ab, and the second set of angle-arc puzzles written by students. You may omit puzzle #1 if you find it too difficult, but I definitely expect you to solve puzzles 2 and 3. Note: In #17, please correct the first sentence by inserting the words “if and” before the word “only.” The problem should read, “A quadrilateral can be inscribed in a circle if and only if a pair of opposite angles are supplementary.” Super bonus (optional): Prove the converse of Theorem 93 on p. 487. This can be done by contradiction, believe it or not, using Theorem 93 as a lemma. This is the only example I can think of in which the converse of a theorem can be proved by using the theorem itself. (Normally, such a procedure would result in circular reasoning.) If you can do this without assistance, I will grant you a certificate of exemption from several homework assignments. This offer is valid, however, only if you first complete problems #11, 17, and 19ab above, plus puzzles 2 and 3 from the second set of puzzles.
T 3/9/010	Because of technical difficulties with the server, today’s assignment could not be posted in time. Therefore, you have no additional HW requirement, but you should strive to complete the previously assigned problems.
W 3/10/010	HW due: §10.9 #3, 5, 7, 13, 14, 17, plus as many of the review problems on pp. 505-509 as you can do in preparation for Thursday’s test. Most of the answers are available at hwstore.org, but you should try to obtain the maximum educational benefit by doing the work yourself and checking afterward. In class: Review.
Th 3/11/010	Test (100 pts.) through Chapter 10. Note that the power theorems in §10.8 are included, even though we did not specifically do HW from that section. Example power theorem problems can be found in #3 on p. 505.
F 3/12/010	No additional HW due. E period will meet in MH-313 with Ms. Dunn. F period will meet in MH-314 with Mr. Kelley. In class: You will watch the Simpson’s Paradox video (topic #1 from Mr. Hansen’s video collection). A quiz Monday covering the video is possible. If you are absent today, you are still responsible for viewing and learning the content of the video.
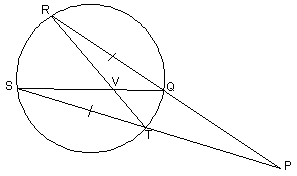
M 3/15/010	HW due: Prepare for possible quiz on video from last Friday; read §§11.1 and 11.2; write a 2-column proof for the problem below. The curved figure is a circle, but you may not assume that V is the center. There are many ways to prove this: CPCTC with subtraction, power theorems, auxiliary lines with HL, and proof by contradiction are four ways that students have found so far, and maybe you can even find a fifth way. You can earn a bonus point if you write up more than one method that works (assuming that your work is neat, correct, and in proper 2-column proof format). Given: QR = TS Prove: PQ = PT
T 3/16/010	HW due: Because of a technical glitch in posting the assignment on time, this work is not due until Wednesday. Read §§11.1 and 11.2; write §11.1 #3, 5, 8, 10, 15, 17. Be sure to use the “formula, plug-ins, answer with units” style that we discussed in class. For example, here is what I would accept for #3b: perim. = 2l + 2w = 40 wlog, assume l = 6 2(6) + 2w = 40 12 + 2w = 40 2w = 28 w = 14 A = lw = 6(14) = 84 sq. units Note that the final answer must include units and should also be circled or boxed to make it easy to check.
W 3/17/010	HW due: Do yesterday’s assignment, plus you can earn up to 2 bonus points if you do the following problem. St. Patrick’s Day Bonus Problem: Compute the area of the “shamrock” figure below, which is formed from 4 overlapping congruent circular regions of radius 3 cm. Each of the overlapped regions has an area of cm^2. Give your answer both in exact form (using ) and as a reasonable ballpark estimate.
Th 3/18/010	HW due: Read §§11.3 and 11.4; write §11.2 #1, 3, 4, 7, 8, 9, 14, 17.
F 3/19/010	HW due: Write §11.3 #1, 2, 3, 6, 7, 11, 13, 17. Additional problems due after spring break: Write §11.4 #2, 4, 7, 10, 11. In class: We will attempt to reserve the last 15 minutes for construction of the solar system model. If we can get through all of the §11.3 and §11.4 problems today, there will be no additional HW during spring break. Focus, focus, focus!

---

Return to the Geometry Zone

Return to Mr. Hansen’s home page

Return to Mathematics Department home page

Return to St. Albans home page

Last updated: 20 Mar 2010