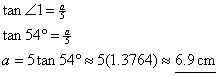|
M
2/1/010
|
HW due: Read §9.10; memorize 3 lines of the table on
p. 424 (as described below); write §9.8 #14-17 all. Be sure to make a large
sketch for each problem. Tiny sketches are no good!
The lines of the table on p. 424 that I want you to memorize are the lines
for 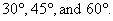 It’s not as bad as
it sounds, though, because you can use your known facts about special
triangles. It’s not as bad as
it sounds, though, because you can use your known facts about special
triangles.
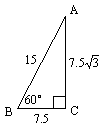
First, sketch a  triangle as shown
above. You can give it any lengths that you wish, so long as they conform to
the rules we learned: short leg equals half the hypotenuse, long leg is triangle as shown
above. You can give it any lengths that you wish, so long as they conform to
the rules we learned: short leg equals half the hypotenuse, long leg is 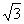 times the short leg. times the short leg.
Then, compute the sine, cosine, and tangent of 30 degrees (namely, 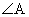 ). By applying the SOHCAHTOA definitions, you get ). By applying the SOHCAHTOA definitions, you get
sin 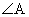 = = 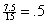
cos 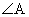 = = 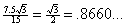
tan 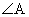 = = 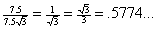
(By the way, it is fine with me if you memorize the simplified radical
expressions instead of the decimals.)|
In a similar way, you can find the sine, cosine, and tangent of 60 degrees
(namely,  ): ):
sin  = = 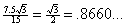
cos  = = 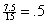
tan 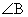 = = 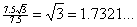
As for 45 degrees, please recall that we did the sine, cosine, and tangent in
class last Friday.
|
|
|
T
2/2/010
|
HW due: pp. 429-433 #1*, 3**, 4, 5, 6***, 10, 13,
14, 16, 24, 27, 31, 33, 35. If you cannot finish all of these in one night,
do as many as you can for Tuesday and bring the rest to the test on Wednesday
for a quick spot-check. You are responsible for all of the topics represented
in these problems, as well as the basics of sines, cosines, and tangents. (We
will do more with trigonometry later in the week.)
* For #1, please copy the diagram and label the lengths with lower case
letters as follows: EH = a, EF = b, EG = s, HG = c, GF = d, and HF = e. That will make it easier for us to go over answers in class.
For example, #1(a) becomes
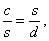 from which we get from which we get 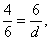 which we can readily
solve for d. which we can readily
solve for d.
** For #3, simply name the family
and state the answer. No diagram is
required.
*** For #6, answer the problem two ways: (a) assuming Vail starts in Vail,
Colorado, and (b) assuming Vail starts precisely at the South Pole.
|
|
|
W
2/3/010
|
HW due: Finish your review problems. As was announced in class,
bring your HW sheets to the test so that they can be spot-checked while you
take your test. Note that many of the solutions are available on the Q3
(2/2/2009) entry at hwstore.org, and you
are permitted to consult that site for inspiration.
Test (first 50 pts. only) through
§9.9. Familiarity with the table on p. 424 is also assumed. The only
entries that you are required to memorize are the lines for 30 degrees, 45
degrees, and 60 degrees, but you should also be aware that
(1) the tangent function for acute angles is always greater than the sine
function,
(2) the sine increases as the angle increases, reaching a limiting value of 1
as the angle approaches 90 degrees,
(3) the cosine function decreases as the angle increases, reaching a limiting
value of 0 as the angle approaches 90 degrees, and
(4) the cosine of any acute angle equals the sine of the complement. (Hence the name: “cosine.”)
|
|
|
Th
2/4/010
|
HW due: Same as yesterday. Because there was insufficient
time to perform a HW check during the short period yesterday, we will do the
HW check today. Bring your review problems (see 2/2 calendar entry).
Remember, many of the solutions are available on the Q3 (2/2/2009) entry at hwstore.org, and you are permitted to consult
that site for inspiration.
Test (second 50 pts.) on same material
as noted above.
|
|
|
F
2/5/010
|
No additional written HW is due today. Any older assignment
from the second semester may be re-scanned, however. F period will not meet
today because of the approaching “Snowpocalypse.”
|
|
|
M
2/8/010
|
No school because of the Snowpocalypse!
However, there will be an assignment for Tuesday, Wednesday, and Thursday, regardless of whether or not St. Albans is
in session. Be sure to check here each day by 3:00 p.m. for the following
day’s assignment. If time permits, I may post some additional video links or
other resources to help you learn the material without having the benefit of
classroom discussion. If the textbook and other materials prove inadequate,
please see my contact information and call me on
my 24-hour number.
|
|
|
T
2/9/010
|
HW due: Reread §9.10 (originally assigned for 2/1); write
p. 323 #26 and problem #99 below. The first problem (#26) was too hard when
we originally did that material, but you should be able to do it now. (Do not
call me and say, “I can’t do it.” The first thing I will ask you is what you
have tried so far, and if you say, “I don’t know where to start,” I will
politely ask you to call back later when you have tried something.) Here is
the second problem:
99.
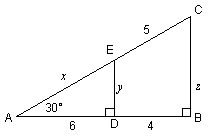
(a) Prove that the diagram above is impossible. In other words, you can have
a 30-degree angle at vertex A, or you can have EC = 5, but you cannot have
both. Hint: A proof by
contradiction would be appropriate here.
(b) Copy the diagram. Erase the number 5, and compute x, y, and z.
(c) Copy the entire diagram a second time, including the marking showing EC =
5. Erase the  marking at vertex A,
and compute x, y, and z. You may wish
to use a calculator, because the values for y and z are a bit
messy. marking at vertex A,
and compute x, y, and z. You may wish
to use a calculator, because the values for y and z are a bit
messy.
Note: This assignment is due Tuesday
and will be scanned when we return to school, regardless of whenever that
might be.
|
|
|
W
2/10/010
|
HW due:
Read the Mini-Lecture; write §9.10 #2, 4,
5, 9, 10, 14. Problems 2a and 14 are done for you below, and you may copy the
work. For #2b and #2c, be sure to use the exact same type of notation that I
used in #2a.
I have created a two-part video (see topic 7 at www.StudyOfPatterns.com/videos) that
instructs you on exactly how to write and solve trigonometric equations,
including problems that involve inverse functions. I would like everyone to
watch this video. If it is paced too slowly, you can skip over some of the
examples. If it is paced too quickly for you, please watch it as many times
as necessary until it starts to make sense.
2(a). 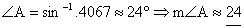
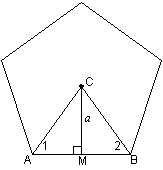
14. Refer to the diagram above. Let C be the center of the regular pentagon,
so that AC = BC. Since 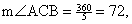 and since and since 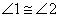 by ITT, we know that by ITT, we know that
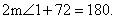 Simple algebra then
gives Simple algebra then
gives 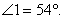 [A common student
error is to label [A common student
error is to label 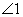 as as 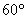 without thinking,
but the correct angle is without thinking,
but the correct angle is 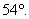 ] Since AB = 10 cm (given) and ] Since AB = 10 cm (given) and 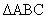 is isosceles, we
know AM = 5 cm. is isosceles, we
know AM = 5 cm.
Trigonometric equation for finding a,
the apothem (pronounced AP-uh-themm):
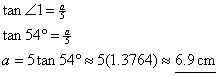
Note: This assignment is due Wednesday
and will be scanned when we return to school, regardless of whenever that
might be.
|
|
|
Th
2/11/010
|
HW due:
Write §9.10 #17*, p. 436 #20, p. 558 #37**.
* For #17, write the terms slant height
(a), lateral edge (b), and dihedral angle (c) on your diagram, with
arrows to indicate what the terms refer to. Show your work, including proper
inverse notation where appropriate.
** For #37, it looks as if you must first find the bases (b1 and b2), since the area of a trapezoid is given by the
formula 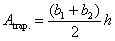 . .
However, there is a much easier formula for the area of a trapezoid, namely 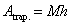 , where M, the median of the trapezoid, is defined to
be the average of the bases, i.e., , where M, the median of the trapezoid, is defined to
be the average of the bases, i.e., 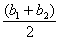 . I am especially fond of this Mh formula. Do you know why? . I am especially fond of this Mh formula. Do you know why?
It turns out that in #37, solving for the median, M, is the only way
to go, since believe it or not, finding numeric values for b1
and b2 is impossible. Let X denote the point where the
diagonals cross, and let A and B denote the midpoints of the two bases. Use
trigonometry to write expressions for AX and BX (that takes a while, and you
can’t actually find values for AX and BX this way, only expressions). Since
we know AX + BX = 18, you can write your expressions for AX + BX and set them
equal to 18. If you do this correctly, a little bit of algebra will give you M, the median of the trapezoid.
Multiply by 18, and you’re finished.
There are at least two other methods for solving #37 without using
trigonometry, but you would have to look at the problem in precisely the
right way. (One method, in fact, cleverly sidesteps the trapezoid area
formula altogether!) However, I would prefer that you use the trig method
first, since it is more straightforward, and then later on (if you wish) you
can try finding more interesting methods.
Note: This assignment is due Thursday
and will be scanned when we return to school, regardless of whenever that
might be.
|
|
|
F
2/12/010
|
No school (teacher work
day).
|
|
|
M
2/15/010
|
No school (holiday).
|
|
|
T
2/16/010
|
Normal school day. The
three assignments from last week are due today. I would also strongly
recommend that you watch the video entitled “Snowpocalyptic Trigonometry”
(topic 7 at www.StudyOfPatterns.com/videos).
Since everyone will be required to watch this video by Wednesday, you might
as well take care of it early if you can.
|
|
|
W
2/17/010
|
Double Quiz (20 pts.) on the “Snowpocalyptic Trigonometry” video. Be sure
to watch both parts (topic 7 at www.StudyOfPatterns.com/videos).
The total running time is approximately 46 minutes.
During the quiz, you will be provided with a trig table identical to the one
on p. 424. However, you will not be able to use the textbook during the quiz.
If you wish, you may use a note sheet (single page, max. size 8.5 inches by
11 inches) during the quiz. As for any calculations during the quiz, they
will be either something you can do in your head or something that you can
leave unsimplified.
|
|
|
Th
2/18/010
|
HW due: Read §10.1; write
the following problems, showing sketch,
trigonometric equation, and solution steps for each problem after except for
#1. For #1, you will need to use a compass or compass fingers, plus a
straightedge. (An edge of a credit card will work fine.)
1. Construct a circle. Repair the hole (if any) made by your compass so that
you cannot see exactly where the center is. Then, use Theorem 76 to come up
with a procedure for constructing the center. Hint: Two intersecting lines determine a point.
2. Barun’s humongous SUV, seen in the distance as it approaches along level
ground, has an angle of elevation of 2 degrees. The vehicle is 7 feet tall.
How far away is it?
3. A radio tower is located in the middle of a flat field. The angle of
elevation, measured from a point 250 meters from the base of the tower, is 63
degrees. How tall is the tower?
4. The cities of Arrggh, Blarrggh, and Centralia are located in the
configuration of a right triangle. Arrggh is 15 km due east of Centralia, and
Blarrggh is 22 km due south of Centralia. Solve the triangle. (In other
words, find the distance from Arrggh to Blarrggh, as well as the angles at
Arrggh and Blarrggh.)
|
|
|
F
2/19/010
|
HW due: Watch the
“Dangerous Symbols” video (topic #5 at www.StudyOfPatterns.com/videos).
|
|
|
M
2/22/010
|
HW due: Read §§10.2 and
10.3; write §10.3 #1, 2, 3.
Remember, arc measure is always defined to equal the measure of the central
angle. Arc length, on the other
hand, is found by multiplying circumference, namely 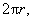 by a prorating
factor equal to by a prorating
factor equal to 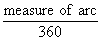 . .
Example: In #4 on p. 455, let QB =
5 meters. Then find (a) the arc measure and (b) the arc length of arc AB.
Solution: (a) By the central angle
rule, arc measure = 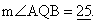
(b)
Arc length = (circumf.)(prorating factor) = 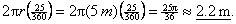
|
|
|
T
2/23/010
|
Optional HW due: I strongly
recommend that you choose a selection of odd-numbered review problems from
the ends of Chapters 9 and 10, plus all of the problems listed below.
p. 435 #17
p. 436 #22abc
p. 436 #22d defined as follows: Solve 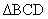 . .
p. 501 #3abcd
p. 505 #4abc
In class: Go over all review problems listed above plus any other questions
you have.
|
|
|
W
2/24/010
|
HW due: Read §10.4; write §10.4
#7, 8. This is a difficult section, and you will probably want to read the
box on p. 462 twice.
|
|
|
Th
2/25/010
|
Test (100 pts.) through §10.3.
The 6 theorems in §10.2 (p. 453) can be linked to the theorems in §10.1 (p.
446) to make a quadruple biconditional as follows:
Two chords are equidistant from the center of a circle iff
those chords are congruent iff
the arcs intercepted by those chords are congruent iff
the central angles associated with those arcs and chords are congruent.
Remember, “iff” (if and only if) is a synonym for the double-headed arrow (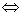 ). A double-headed arrow is the way that we indicate
equivalence (i.e., definition or biconditional statement). ). A double-headed arrow is the way that we indicate
equivalence (i.e., definition or biconditional statement).
For now, it is enough to know the basic statements of the theorems and a few
simple applications. Problem #6 on p. 455 is a good example of the difficulty
level you should be able to handle.
|
|
|
F
2/26/010
|
HW due: Please get some
additional sleep!
In class: A contest that people who have slept well should have a better
chance at winning.
|
|