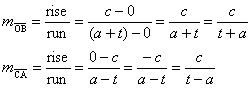|
M
1/4/010
|
Classes resume.
HW due: Click here for the study tip
sheet, which includes links of its own to a practice exam and answer
keys. Be sure to study before you
take the practice exam, since the practice exam does not include every
possible type of problem and does not include any practice proofs. The
real exam will include a pair of 2-column proofs, worth 22% of your exam
grade or 4.4% of your entire semester grade.
If you have time, I strongly recommend that you watch the 11-minute video from
December 18 a second time. You need to understand how Flatland works, how
one can “fold” through a higher dimension in order to “pop” from one place to
another in a lower dimension, and the basics of how higher dimensions can be
generated. Please note, the video respresents only one of many possible ways
in which higher-dimension spaces can be envisioned.
|
|
|
T
1/5/010
|
HW due: Read §§8.4 and 8.5; write §8.3 #9, 13, 16,
§8.4 #9, 18, 19, 20.
|
|
|
W
1/6/010
|
HW due: Write §8.5 #1-8 all, 14, 15, 22. Also, in
#3, prove that the figure is actually impossible.
|
|
|
Th
1/7/010
|
Review. No additional HW due. However, older items
(second quarter only) may be re-scanned.
In class: Discussion of analogical reasoning, statistical reliability, and
psychometrics.
For example, consider the analogy
hand : foot :: glove : ______
That analogy is equivalent (by exchange of means) to the following analogy,
which I find somewhat easier:
hand : glove :: foot : ______
The reason I find the second one easier to solve is that I can say to myself,
“A hand is COVERED by a glove, just as a foot is COVERED by a sock.” Answer:
sock.
Analogical reasoning is essential for success in college. However, the SAT
people, responding to pressure from students (many of whom complained that
analogies were too difficult and could not be easily “gamed” by taking SAT
prep courses), dropped analogies from the SAT a few years ago.
Regarding reliability (repeatability) of test scores, it is interesting that
the SAT people market the test to students by encouraging students to take
the test multiple times (thus increasing revenue) so as to maximize the
chance of getting a higher score. In effect, they are telling students that
the reliability of the test is low. At the same time, they are saying to
colleges and universities that the SAT is a reliable admissions test, since
the same student will get virtually the same score if he repeats the test.
Hmmmmm. That’s one of the strange things that happens when you have two sets
of customers (students and colleges) who have differing desires regarding the
test. Students want a high score, and colleges want a meaningful score to
help them differentiate among students who are applying for admission.
It’s a shame, in my opinion, that the analogical reasoning parts of the SAT
have been dropped. I think one could make the case that those analogy
sections were the most relevant of all when it comes to designing a college
admissions test.
Continuing on the topic of reliability and psychometrics, we discussed how a
test is going to be reliable, if at all, only in the band where you have
adequate data. If one student scores a 75 and another student scores an 85,
you can usually say with some confidence that the second student probably
studied harder or learned the material somewhat better. (We are assuming, of
course, that the test is well designed to measure what needs to be measured.)
However, if one student earns a 60 and another earns a 20, all you can really
say is that both students failed. You cannot say that the student with the 20
failed “three times worse” than the student with the 60, since a 20 is so far
out in the “tail” of the distribution of scores that accurate comparisons
simply cannot be made. Similarly, an 800 is the highest possible score on each
section of the SAT. Someone may have a raw score that would place him 3 and a
half standard deviations above the mean, but his score is not reported as
850—it is simply reported as 800, since there are so few students in the
extreme right “tail” of the distribution that there is no reliable way of
comparing them. Another example we discussed is IQ tests, which are extremely
unreliable above about 150 or so. If someone claims to have an IQ of 200,
he’s probably lying, because if he really had an IQ of 200, he would surely
be smart enough to know that an IQ of 200 is unreliable and essentially
meaningless.
|
|
|
F
1/8/010
|
Review.
|
|
|
Th
1/14/010
|
Optional
Review/Q&A Session, 2:00 p.m., MH-313. Come and stay as briefly or as long as you wish. Drift in and out if
you like, and feel free to invite your friends from Ms. Dunn’s classes or Mr.
Andreoli’s class to attend as well. I will stay as long as there are people
asking questions.
|
|
|
F
1/15/010
|
Midterm
Exam (20% of your semester grade), 8:00−10:00 a.m., Trapier Theater.
What to bring: several sharpened
pencils, good eraser.
Optional: straightedge.
Not allowed in the examination area:
scratch paper, note paper, compass, cell phone, electronic devices.
Students in Ms. Dunn’s classes and Mr. Andreoli’s class will be allowed to
use a calculator, but you may not use a calculator. If an answer to a
free-response problem involves messy arithmetic, you may leave it
unsimplified unless the problem says that simplification is required. For
example, if the answer to a problem is 15 times 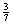 , with the entire quantity raised to the 4th power, you may
simply write (15 · , with the entire quantity raised to the 4th power, you may
simply write (15 · 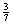 )4. )4.
Format of the exam:
Part I: Always/Sometimes/Never with Explanation (6 questions, 3 pts. each,
18% of exam)
Part II: Multiple Choice (20 questions, 2 pts. each, 40% of exam)
Part III: Problems (5 questions, 4 pts. each, 20% of exam)
Part IV: Two-Column Proofs (2 questions, 10 + 12 pts., 22% of exam)
In Part I, each question is worth 3 points: 1 point for the answer and 2
points for a complete diagram and/or a short mini-proof that explains your
reasoning. A cryptic diagram without proper markings, which is what you may
have been putting on your chapter tests, will not qualify for full credit.
In Part II, there is no partial credit,
which means that you must read and evaluate all 5 possible answers (A, B, C,
D, and E) for each question to make sure that you have chosen the best
answer. If you guess, play hunches, or hurry through Part II, you cannot earn
a good grade on the exam. Please note that multiple choice for math is much
harder than multiple choice for most other subjects. For examples of
questions, please see the midterm exam
tip sheet, which includes links to a practice exam and answer keys.
In Part III, adequate work is required, and your final answer must be
circled. Cryptic, illegible, or incomplete responses will not qualify for
full credit, even if the final answer happens to be correct.
In Part IV, the proofs are of medium difficulty, and you are expected to
complete both of them.
Points may be deducted for any disturbance during the exam. No hints will be
provided, and if you ask a question that is already answered by the
instructions on the exam, points may be deducted. The reason for this harsh
rule is that there will be about 80 people in Trapier Theater, and it is
unacceptable to have a disturbance and teachers moving around every time
someone wishes to have a question answered. If you find a typographical
error, simply mark it and keep working.
Be sure to get lots of sleep the night before the exam! Sleep will help you
more than cramming. In fact, cramming for a math exam is pointless, since if
your skills are not solid, you would have to be a genius to learn them at the
last minute.
|
|
|
M
1/18/010
|
No school (holiday).
|
|
|
T
1/19/010
|
No school (teacher work day).
|
|
|
W
1/20/010
|
Classes resume. Welcome to new F period student
Camyar!
|
|
|
Th
1/21/010
|
HW due: Read §9.2; write §9.1 #1-9 all. Camyar, please
follow the HW guidelines link at the top of the schedule.
|
|
|
F
1/22/010
|
HW due: Read §9.3; write §9.2 #1, 2, 6, 7, 8, 10.
|
|
|
M
1/25/010
|
HW due: Read §9.4; write §9.3 #1, 2, 3, 5, 9. Many of
the problems are solved or half solved below. You may copy my work if you
wish in order to get started. (The rest of the work must be your own.)
Theorem 68 (p. 378) can be summarized as follows:
a. When an altitude is drawn to
the hypotenuse of a right triangle, all three triangles are similar by AA~.
(That is, the big triangle is similar to each of the two smaller triangles,
and the smaller triangles are similar to each other.)
b. By similarity, 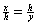 where x and y are the divided parts of a hypotenuse, and h is the length of the altitude that creates those lengths of x and y when the altitude is drawn to the hypotenuse. where x and y are the divided parts of a hypotenuse, and h is the length of the altitude that creates those lengths of x and y when the altitude is drawn to the hypotenuse.
c. (I call this the “Near Chunk,
Whole Chunk” principle.) In any right triangle, let x and y be defined as
in part b. Note that one of the
legs is adjacent to x, and the
other leg is adjacent to y. STOP!
LOOK! YOU MUST UNDERSTAND THIS BEFORE CONTINUING!
If we let a denote the leg that is
adjacent to x, then a2 = x(x + y), which I call “Near Chunk Times
Whole Chunk of the hypotenuse.”
By the same token, if we let b
denote the leg adjacent to y, then b2 = y(x + y). Once again, the same principle of
“Near Chunk Times Whole Chunk” is satisfied.
1.(a) In the diagram, EH is playing the role of x, HG is playing the role of y,
and HF is playing the role of h.
Therefore, 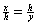 becomes becomes 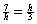 . Cross-multiply and solve for h. Answer: h = HF = . Cross-multiply and solve for h. Answer: h = HF = 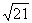 . .
(b) Hint: EF is
playing the role of a. Use part b from the theorem summary above.
2.(a) Since 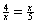 , we know x2
= 20; therefore, 2x = , we know x2
= 20; therefore, 2x = 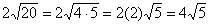 . .
(b) Hint: First
use “Near Chunk, Whole Chunk” to write y2
= 4(4+5).
3.(a) Since 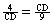 , we get (CD)2 = 36. Therefore, CD = 6. , we get (CD)2 = 36. Therefore, CD = 6.
(b) Hint: First
use “Near Chunk, Whole Chunk” to write (AC)2 = 4(16).
5.(a) Since 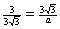 , cross-multiplication gives 3a = , cross-multiplication gives 3a = 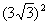 = 27. Therefore, a = 9. = 27. Therefore, a = 9.
|
|
|
T
1/26/010
|
HW due: Read §9.5 and prepare for an open-notes quiz;
write all of your previously assigned written problems to perfection.
|
|
|
W
1/27/010
|
HW due: Read §9.6; write §9.4 #1, 2, 3, 6, 7, 8, 11,
§9.5 #1, 9, §9.6 #1-5 all.
For §9.6, no sketches are required; simply write the answers. For the other problems,
full work (diagram, formula, plug-ins, answer) are required as always.
|
|
|
Th
1/28/010
|
HW due: Read §9.7; write §9.6 #14, §9.7 #1-5 all,
22.
Hint: For any coordinate geometry
proof (e.g., #14), the steps are as follows:
1. Make a “wlog” diagram with coordinates labeled.
2. Use slope formula, midpoint formula, distance formula, or other suitable
formulas to prove the claim.
3. Write Q.E.D. or the Halmos sign.
For example, here is a coordinate geometry proof that the diagonals of a
rhombus are always perpendicular:

Wlog, place one vertex of rhombus OABC at the origin as shown. Since all four
sides have length a by def. of
rhombus, we know that t2
+ c2 = a2 in the diagram. In other
words, t2 − a2 = −c2. (This last equation is
a fact that we will save until the very end.)
To show that 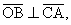 we need to compare
slopes, using the slope formula. [In problem #14, the proof concerns
distances, which means that you would use the distance formula.] we need to compare
slopes, using the slope formula. [In problem #14, the proof concerns
distances, which means that you would use the distance formula.]
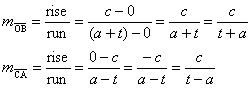
Are we finished? No, we need to show that the two slopes, namely 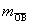 and and 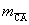 , are opposite reciprocals. We know that two numbers are
opposite reciprocals iff their product equals −1. Let’s try it and see
what happens! , are opposite reciprocals. We know that two numbers are
opposite reciprocals iff their product equals −1. Let’s try it and see
what happens!
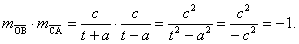 
Note: The substitution in the
next-to-last step was provided by the equation we saved from above, which is
true by the Pythagorean Theorem.
|
|
|
F
1/29/010
|
HW due: Read §§9.8 and 9.9; memorize the three-part
definition on p. 419 (memory aid: SOHCAHTOA);
write §9.8 #5, with the following additions:
(a) Write on your homework paper that AD = side length of base.
(b) Write that YR = apothem of base. [The word apothem is pronounced with the accent on the first syllable:
AP-uh-themm.]
(c) Write that PR = slant height, PD = lateral edge, and PY = height.
Free Bonus App: If you own an
iPhone or iPod Touch, please download the program entitled BallparkIt, which is a calculator for
learning trigonometry. The cost is $1.99, but if you download it, I will
reimburse you for the cost.
|
|