Monthly Schedule

(Geometry, Periods E and F)

Th 10/1/09	HW due: Read §2.6; write §2.6 #3, 4, 10, 14, 15, and the following problem. 99. In your own words, explain how to keep track of whether “mult. prop.” or “div. prop.” is an appropriate reason to use in a proof, or whether a more appropriate reason would be “def. of bis.” or “def. of tris.” You can use the concept of “one situation, two situations” that we discussed in class, or you can make up your own. A short paragraph is expected.
F 10/2/09	HW due: Read §2.7; write §2.7 #4, 7, 8, 9, 14, 18.
M 10/5/09	HW due: Read §2.8; write §2.8 #4, 7, 8, 10, 11, and a selection of review problems from #1-38 on pp. 105-109. Do as many as you can, since all are fair game for our next test. If you get stuck, you may review the solutions here, but only after you have tried hard! (If you peek too soon, you are simply wasting time, since you are not challenging yourself and learning, and then you won’t do very well on the test.)
T 10/6/09	HW due: Finish your review problems. If you have time, I strongly recommend reworking them under time pressure in order to prepare for the test. All solutions are posted here, but do not peek at the solutions until you have struggled hard! Otherwise you are not preparing yourself properly for the test. People who have not yet finished their corrections from the first test, and believe it or not, there are several people in that category, need to turn those in today for partial credit.
W 10/7/09	Test (100 pts.), cumulative through Chapter 2. All material from Chapters 1 and 2, as well as all material discussed in class, is fair game for this test. That is why it is so important that you finish your Chapter 1 corrections and work to understand them if you have not already done so. Five students have a Cities test during D period today, but that is all right. You are required to take up to two tests in a day. Any other tests that you may have are lower on the priority scale per school policy, and you are allowed to arrange make-up tests with those teachers so that you do not have three tests in the same day.
Th 10/8/09	HW due: Read §§3.1 and 3.2; write §3.1 #1, 2.
F 10/9/09	HW due: Get lots of sleep.
M 10/12/09	Columbus Day (no school).
T 10/13/09	HW due: Read §§3.3 and 3.4; write §3.2 #4, 5, 8; §3.3 #9, 11, 13.
W 10/14/09	HW due: Read §3.5; write §3.4 #1, 4, 6, 12. (Write a 2-column proof for #4 and #12.)
Th 10/15/09	HW due: Read §3.6; write §3.5 #3, 4, 7, 20, 21. (Problems 20 and 21 are given below.) 20.(a) What is the only type of triangle in which the center of gravity, incenter, circumcenter, and orthocenter are all located at the same point?      (b) Roughly sketch such a triangle, showing its inscribed and circumscribed circles.
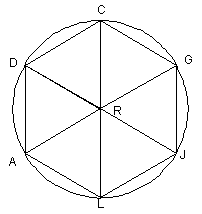
	21. Given: Circle R     Prove:
	Important: During the day today (Thursday), unless your name is on the list below, please ask your teachers if you may attend tomorrow’s field trip to the Solar Decathlon exhibit on the Mall. The following students have class conflicts and should not plan on attending: Duncan, Henry, Marcos, Peter, Josh, and Connor.
F 10/16/09	HW due (E period): No additional written work is due. Please fill in the gaps in your previous assignments. HW due (F period): View this animated presentation that I told you about in class, in order to learn how to construct a perpendicular bisector. With any additional time you have, fill in the gaps in your previous assignments. Field Trip to the Mall (note changed time and list of students who cannot go): Leave on bus next to Martin Gym at 10:10 a.m. sharp (15 minutes before end of B period). We will take whoever is on the bus at 10:10. We will be gone during all of C period and will return to STA at the start of D period. Your teachers have been asked to excuse you from C period and part of B period if it is possible for you to miss class without disruption. Duncan, Henry, Marcos, Peter, Josh, and Connor are among those who have class conflicts and will not be able to attend. Quiz: There will probably be a quiz on how to construct a perpendicular bisector. E period students are also free to view the animated video whose link is posted above. Other possible topics on the quiz are SSS, SAS, ASA, SSA (must know why that is invalid), ALTO, ABIC, PBCC, MCCG.
M 10/19/09	HW due: Read §§3.7 and 3.8; write any two of the three exercises below (your choice). 1.(a) What Latin name did we give in class to the bidirectional theorem represented by what your book calls Theorems 20 and 21?    (b) What does ITT stand for? Is that the same as your answer to part (a)?    (c) When you use ITT as a reason in a proof, would you prefer to write “ITT” or to use the pictorial notation shown below? 2. Using a compass and straightedge, carefully replicate Friday’s in-class circumcenter exercise. This time, construct all three perpendicular bisectors of a random triangle called . (Note: The third perpendicular bisector provides a cross-check on the other two.) The point where the perpendicular bisectors intersect is the circumcenter. Use the circumcenter you found to construct the circumcircle, which is the circle passing through points S, T, and A. 3. Using a thin sheet of cardboard (for example, the back of a cereal box), mark a region in the shape of a random triangle called . Do not cut out the triangle yet. Use the animated procedure from last week (or, if you do not have a compass, I will allow you to use a ruler) to find the midpoint of each side, and mark the midpoints of the triangles’ sides as M1, M2, and M3. Use a straightedge to construct the medians of . When you cut out the triangular region, does it balance at the point where the medians intersect?
T 10/20/09	HW due: Write §3.6 #2, 4, 6, 13, §3.7 #2, 9, 10.
W 10/21/09	HW due: Write §3.8 #1-9 odd, plus p. 164 #18, p. 167 #18. Answers to the last two can be found here, but please do not peek until you have struggled with the problems.
Th 10/22/09	Test #3 (100 pts.), cumulative over Chapters 1-3 and all material covered since the beginning of the year. For example, the meaning of the Latin phrase Pons Asinorum (Bridge of Donkeys, a.k.a. the Isosceles Triangle Theorem) is among the things you are expected to know, even though it is not discussed in the textbook. You are also expected to have memorized PBCC/ABIC/ALTO/MCCG, which can be found at the 4/29/08 calendar entry. (You will need to scroll down until you get to 4/29/08.) Study aids. The following review problems are suggested: pp. 162-164 #3, 7, 11, 14; pp. 165-167 #23, 24. All solutions except for #11 can be found here, but please do not peek until you have struggled with the problems. A practice test is also available.
F 10/23/09	HW due (as mentioned at the end of the test) was originally supposed to be to read §4.1. However, some people did not hear the announcement, and I forgot to post it by 3:00 p.m. You are of course welcome to read §4.1, since you will need to read it over the weekend anyway. However, by our rule, the HW for Friday is not required, and you have a night of additional sleep if you need it. Yippee!
M 10/26/09	HW due: In keeping with Mr. Wilson’s assembly last Friday that mentioned pursuing new technology ideas for teaching, I would like you to watch video topic #6 (“Hippasus, the First Math Martyr?”) at this video website. Then read §4.1 (reading notes optional) and the handout entitled The X. Total time required should be just about exactly 35 minutes. Be prepared for a discussion or an open-notes quiz.
T 10/27/09	Quest (50 pts.) covering the same material as last Thursday’s test, except that this time you can count on at least one question specifically on HL. This quest will be somewhat easier (i.e., with no ultra-tricky fleems, bleems, treems, or ultra-tricky Always/Sometimes/Never). You will have to think, but if you were prepared last Thursday, you will be just fine. ITT proofs (a.k.a. Pons Asinorum) and the PBCC/ABIC/ALTO/MCCG facts will be on the quiz, as will Karl’s excellent A/S/N question.
W 10/28/09	HW due: Read §4.3 (the RAT); write §4.2 #1-15 all with no proofs. Do the diagrams, “given,” and “prove” statements only.
Th 10/29/09	HW due: Read §4.4; finish up §4.2 #1-15 all with no proofs; write §4.3 #2, 6, 10ab. For §4.3 #2, you need to provide a diagram, the “given” statement, the “prove” statement, and a proof. For §4.3 #10, proceed as in #6 for both (a) the problem as stated and (b) the converse of the problem stated. In other words, for #10, you need to do two things: (a) Given: is the median to the base of isosceles       Prove: (i.e., is the altitude to the base) (b) Given: is the altitude to the base of isosceles       Prove: (i.e., is the median to the base)
F 10/30/09	HW due: Read §4.5 and the story below; write §4.4 #4, 5, 6, 8, 12. The Story of Woody Mr. Hansen’s dog for many years was Woody, a yellow lab/golden retriever cross that came with the house that Mr. Hansen and his wife bought in 1989. Woody was loyal and fearless, with one small exception. He was terrified of storm sewer drains, and if ever there were two storm sewer drains on opposite sides of the street (call the storm sewers A and B), Woody would make himself as thin as possible and would walk straight along the line that was the perpendicular bisector of . The general principle is encapsulated in the Perpendicular Bisector Theorem (PBT) a biconditional theorem that your textbook calls Theorem 24 and Theorem 25. You can think of PBT in the following way: Woody is equidistant from points A and B if and only if Woody is on the perpendicular bisector of . Or, if you prefer to split this into two theorems, you have these: PBT “original”: Two points where Woody is able to make himself equidistant from A and B will determine the perpendicular bisector of . PBT converse: If Woody is equidistant from A and B, then Woody is on the perpendicular bisector of .

---

Return to the Geometry Zone

Return to Mr. Hansen’s home page

Return to Mathematics Department home page

Return to St. Albans home page

Last updated: 03 Nov 2009