|
W
9/9/09
|
First day of class. Discussion of Mr. Hansen’s three rules, fire drill quizzes,
required equipment, what mathematics is, etc.
|
|
|
Th
9/10/09
|
HW due: Visit www.StudyOfPatterns.com/videos and
watch topics 3A and 4; send me a signed
e-mail.
|
|
|
F
9/11/09
|
HW due: Read §1.1 (reading notes are required, as
shown in the HW guidelines); write §1.1 #5-13
all. A re-quiz on the alphabet is likely.
Important: I still need e-mails
from Luke, Mark, and Thomas from the E period class, as well as Jackson,
Marshall, Lloyd, David, Duncan, and Will from the F period class. Please see
my contact information for the address.
|
|
|
M
9/14/09
|
HW due: Read §1.2 (reading notes required); write §1.2
#1-4 all, and write a short paragraph explaining why the following “solution”
to §1.1 #13 is invalid. (Bonus: Can
you find a valid solution?)
Note: I still need e-mails from
Marshall and Will C.
|
|
|
T
9/15/09
|
HW due: Read §1.3 (reading notes required); write
§1.3 #1, 3, 4, 6.
|
|
|
W
9/16/09
|
HW due: Read §1.4 (reading notes required); write
§1.2 #5 (including part b, which was done in class), 9 (making a rough sketch
for each one), §1.3 #8, 9, 13, 18. Note that problem #18 is not in the
textbook but is given below.
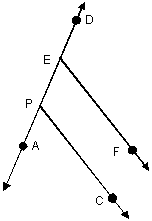
18. Given: In 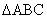 , let AB = x and
BC = y. (AB and BC refer to segment
lengths, as opposed to , let AB = x and
BC = y. (AB and BC refer to segment
lengths, as opposed to 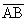 and and 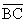 , which refer to sets of points. In other words, we omit
the segment bar if we are referring to a number.) , which refer to sets of points. In other words, we omit
the segment bar if we are referring to a number.)
Find: strict lower and upper bounds for AC. Please make several diagrams to
justify your answers.
(Note: The “strict lower bound” is
the value that is less than any possible answer for AC. The “strict upper
bound” is the value that is greater than any possible answer for AC. For
example, in problem #13, the lower bound for AC was 3 and the upper bound for
AC was 15. Obviously, your answers to #18 will need to have variables in
them.)
|
|
|
Th
9/17/09
|
HW due: Read §1.5; write §1.4 #9, 10, 14, 15,
convert 77.285 degrees to DMS (see example below), and play the Eyeballing Game until you are good at
it. (This may take 10-15 minutes.) Write down your best score. My best score
is 2.28, and you will probably not be able to beat that.
Example of DMS conversion, using the substitution principle:
38.808° = 38° + .808°
=
38° + .808(60')
=
38° + 48.48'
=
38° + 48' + .48'
=
38° + 48' + .48(60")
=
38° + 48' + 28.8"
=
38°48'28.8"
Another example:
16.118° = 16° + .118°
=
16° + .118(60')
=
16° + 7.08'
=
16° + 7' + .08'
=
16° + 7' + .08(60")
=
16° + 7' + 4.8"
=
16°07'04.8"
|
|
|
F
9/18/09
|
HW due: Convert 17°76'07.4" to decimal degrees. Yes, that is a very skimpy assignment. Use
the rest of your time to clean up your older homework problems so that they
are clear, complete, and in proper format.
|
|
|
M
9/21/09
|
HW due (strongly recommended): Spend 50 minutes on
Sunday afternoon working on last year’s first
test for practice. Set a timer for 50 minutes, put away your books, and
try to take the test. We will grade these in class if most of the students
did them. If you do not have time to take the practice test over the weekend,
then do it on Monday night as part of your test preparation, but of course
that may be a little too late.
HW due (required): Read §§1.7 and 1.8 (these were covered on Friday in E
period but not in F period because of the larger number of questions in F
period); write §1.5 #16, §1.7 #5a, 8, 10, §1.8 #1, 2, 4. This assignment is
definitely longer than 35 minutes, but you need to do it. Several versions of
§1.5 #13 are furnished below as graphic files to help you see what is
expected in two-column proofs.
Sample proof #1
Sample proof #2
Sample proof #3
|
|
|
T
9/22/09
|
Test #1
(100 pts.) on all material covered
in class up to this point, including the substitution principle, clock
problems, the key to learning, the reason that schoolwork is graded, etc. To
prepare for the test, please work the 50-minute practice
test under time pressure, and then grade yourself using the scoring key.
Here are the answers to the HW problems we did not have time to cover during
yesterday’s class:
2.(a) Original statement: If each side of a  has length 10, then
the perimeter is 30. (TRUE) has length 10, then
the perimeter is 30. (TRUE)
Converse: If the perimeter of
a  is 30, then each
side has length 10. (FALSE) is 30, then each
side has length 10. (FALSE)
Inverse: If some side of a  does not have length
10, then the perimeter is 30. (FALSE) does not have length
10, then the perimeter is 30. (FALSE)
Contrapositive: If the perimeter
of a  is not 30, then some
side does not have length 10. (TRUE) is not 30, then some
side does not have length 10. (TRUE)
Warning: Correctly negating a
declarative sentence such as “Each side of a  has length 10” is
not easy. For example, you should not say, “Each side of a has length 10” is
not easy. For example, you should not say, “Each side of a  does not have length
10,” because the meaning is unclear. Do you mean that side x is not 10, side y is not 10, and side z
is also not 10? Or do you mean that of the three sides, not all three of them
are 10? What you mean is the latter, but that is not clear unless you use
careful wording, as I have done above. You could also use the following
correct but somewhat awkward wording: “It is not the case that all the sides
are of length 10.” does not have length
10,” because the meaning is unclear. Do you mean that side x is not 10, side y is not 10, and side z
is also not 10? Or do you mean that of the three sides, not all three of them
are 10? What you mean is the latter, but that is not clear unless you use
careful wording, as I have done above. You could also use the following
correct but somewhat awkward wording: “It is not the case that all the sides
are of length 10.”
The confusion is somewhat reminiscent of a classic Saturday Night Live sketch summarized in the first two paragraphs
of this
page. (Don’t read the rest of the link; it is irrelevant.)
(b) Original statement: If an angle is acute, then it has a
measure greater than 0 and less than 90. (TRUE)
Converse: If an angle has
measure greater than 0 and less than 90, then the angle is acute. (TRUE)
Inverse: If an angle is not
acute, then it does not have a measure greater than 0 and less than 90.
(TRUE)
Contrapositive: If an angle
does not have a measure greater than 0 and less than 90, then the angle is
not acute. (TRUE)
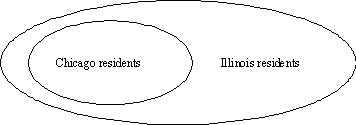
4. Let C = “A person is a Chicago resident.” Let I = “A person is an Illinois
resident.”
The diagram illustrates that 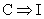 is a true statement. is a true statement.
(a) Given that Penny lives in Chicago, can we conclude that
Penny lives in Illinois? TRUE, since 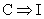 . .
(b) Given that Benny lives in Illinois, can we conclude
that Benny lives in Chicago? FALSE, since that would be reasoning from the
converse. We were not given that 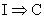 , only that , only that 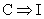 . .
(c) Given that Kenny does not live in Chicago, can we
conclude that Kenny lives in Illinois? FALSE, since he could live outside
both regions shown in the Venn diagram.
(d) Given that Denny does not live in Illinois, can we
conclude that Denny lives in Chicago? FALSE. In fact, since the
contrapositive of 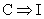 is is 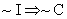 , precisely the opposite conclusion is true. We can
conclude that Denny does not live in Chicago. , precisely the opposite conclusion is true. We can
conclude that Denny does not live in Chicago.
|
|
|
W
9/23/09
|
HW due: Read §2.1; write §2.1 #2, 3, 4, 8, 9, 11.
|
|
|
Th
9/24/09
|
HW due: Read §2.2; write §2.4 #12, §2.2 #3, 4, 6, 7,
11, 18, 19. You may find this
entry from last year’s HW store helpful. (In fact, if you need to, I will
give you permission to copy the solution to #12.)
Additional HW due (E period only): Correct your test, using a different color
of ink and a separate sheet if necessary. If you do not finish by today, you
may turn this in on Monday.
|
|
|
F
9/25/09
|
Centennial day of community service (no class).
Arrive at school between 7:30 and 7:45 a.m. carrying a water bottle with your
name on it. Lunch will be furnished.
|
|
|
M
9/28/09
|
HW due: Read §§2.3 and 2.4; write §2.3 #5, 6, 13,
14, §2.4 #1-7 all.
Also write corrections (using a different color of ink) for your test from
last week. If there is insufficient room on the test paper itself, use a
fresh sheet. Please write, “I should have . . .” or “I realize now that the
method is to . . .” when you have figured out what the problem was asking you
to do.
If you would like a fresh copy of the test, you can download an E period test or an F period test for additional practice.
For problem #12, the shortest (and in some sense, best) proofs were 3 steps
long. These steps are reproduced below, with no reasons given. You will need
to think of the correct reasons when you write up your corrections.
1. Angles BCA and BCD are right angles.
2. Angles BCA and BCD are congruent.
3. Ray CB bisects angle ACD. (Q.E.D.)
|
|
|
T
9/29/09
|
HW due: Nothing new, in theory. However, make your test
corrections 100% neat and wonderful. They will be graded more closely this
time. No shortcuts, no excuses. Work hard, be nice, and remember that there
is no finish line. (I borrowed all these slogans from the KIPP School, but
they are certainly applicable, don’t you think?)
With any remaining time that you have, patch up the holes and gaps in your
previous homework assignments. Be prepared for a random spot-check covering
previously assigned material.
|
|
|
W
9/30/09
|
HW due: Read §2.5; write §2.5 #1, 2, 4, 14, and the
problem below.
20. Given: In the diagram, 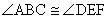 . What can we conclude, and why? . What can we conclude, and why?
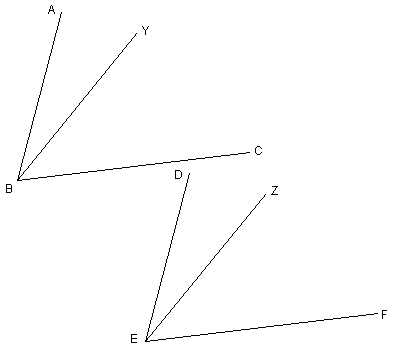
|
|


