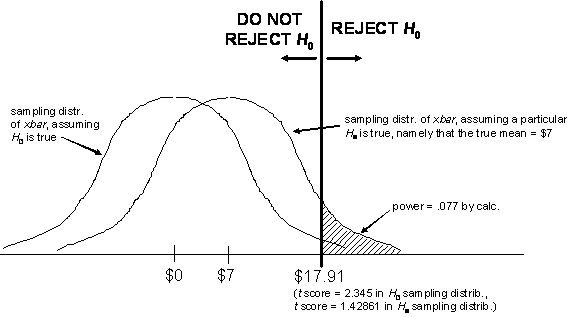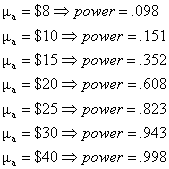Monthly Schedule

(STAtistics, Period D)

M 2/209	Groundhog Day (review session in my office).
T 2/3/09	The test that was originally scheduled for today has been postponed one day in order to provide time for additional in-class review of the key concepts: PHA(S)TPC, P-value, assumptions for the tests, statistical significance, m.o.e., sampling distributions, Keynesian economics, and the benefit (if not the details) of t procedures. Make sure that you know the guidelines on p. 606 for relaxing the assumptions. SRS is more important than normality, since CLT eventually makes all sampling distributions of indistinguishable from normal* anyway. * Caveats: Unless the underlying distribution is already normal, in which case the sampling distribution of is automatically normal, we need sufficiently large n, along with a finite s.d., in order for CLT to guarantee normality of the sampling distribution of .
W 2/4/09	Test (100 pts.) on all recent material.
Th 2/5/09	No additional HW due today. Use this as an opportunity to get caught up on all previously assigned problems, in case you have any gaps.
F 2/6/09	HW due: Read pp. 544-556; write #10.40 using all steps of PHASTPC (including S).
M 2/9/09	HW due: Read pp. 562-580, including all examples (but omitting exercises), which is about 13 pages of reading altogether; write #10.77 using all steps of PHASTPC (including S). You may use your notes from last Friday as a guide. Remember that your conclusion must be in context.
T 2/10/09	HW due: Read pp. 587-589, 592-596; write #10.82, 10.84, 10.86, and define both power and probability of Type II error in your own words. You may use “Ted” as an abbreviation for “sampling distribution for a particular value of the alternative.”
W 2/11/09	HW due: Read pp. 598-608; write #11.16 with a full PHASTPC in part (a).
Th 2/12/09	HW due: Read pp. 610-627, omitting the exercises; write the following problem. For #11.16, which we did yesterday, compute the power of the t test (assuming = 0.01) against the $7 alternative, i.e., the alternative that says = 7. Remember, denotes the cutoff value for the P-value, i.e., the criterion for locating the boundary between “reject H₀” and “do not reject H₀.”
F 2/13/09	No school (faculty professional day).
M 2/16/09	No school (holiday).
T 2/17/09	HW due: Get plenty of sleep. I would strongly recommend doing all previously assigned HW problems if you have not already done so, since some may be scanned a second time. In class, we will go over the following review problems. You are not required to write these in advance, but you will probably get more out of the class if you have tried some of them. Here is the list: #10.78 (using t procedures with s = 8.0 instead of the unrealistic given assumption of ), #10.81, 11.56, 11.58, 11.59.
W 2/18/09	Test (100 pts.) on everything through p. 627. Pay special attention to PHASTPC procedures, basic estimation of power, Type I and Type II error, and the green box on p. 606. Calculation of the power of the t test is less important than estimation, and there will be no more than one question requiring that type of calculation on the test. A worked example is given below. Example (HW due 2/12/09): Let mean change hypothesized by H₀, namely $0. Let mean change hypothesized by a certain alternative hypothesis, namely $7. We have Since = cutoff value for significance, we have a t* score of about 2.364 (estimated from Table C) or 2.345 (more accurate value from INVT). Therefore, the boundary between “reject” and “do not reject” zones is located at (t)(s.e.) = 2.345 · 7.63675 = $17.90995. Where is $17.90995 located in the H_a distribution, expressed using a t score in the alternative distribution*? The answer is standard errors to the right of the $7 centerline. The area of the H_a distribution that bleeds into the “do not reject” zone is therefore given by ~~tcdf(–99999,1.42861,199)~~ [we have to cross that out since it is calculator notation] or .923 as the probability of Type II error. Power is the complement of that, or .077. The graph below tells the story. If you would like more practice, try estimating the power of the t test against each of the following alternatives (cover the right column before checking your answers):
Th 2/19/09	No additional HW due today.
F 2/20/09	HW due: Read pp. 629-631, look at p. 633 for a maximum of 10 seconds, look at the bottom of p. 638 for a maximum of 20 seconds, read pp. 639-640, 645-647. Congratulations! We have now finished Chapter 11.
M 2/23/09	Thanks to everyone who helped me in my long, exhaustive search for the red gradebook. I turned the campus upside down, looking in every sensible place I could think of (and quite a few nonsensical places as well). I went through garbage cans, took my office apart systematically—you get the idea. Finally, at about 6:10 p.m. Friday, I gave up and left campus, heading for Politics & Prose to buy a new gradebook. On my way to the car, I walked past the Little Sanctuary, which Isaac W. and I had already searched thoroughly, three times altogether. I walked straight to one of the numerous pews where I had been sitting during the sports assembly Friday morning, took a few hymnals and prayer books out of the pew . . . and there it was. Therefore, in celebration of this providential event, I am declaring a No Homework Weekend. No additional homework is due today. Whew!
T 2/24/09	HW due: 1. Write #10.78 (using t procedures with s = 8.0 instead of the unrealistic given assumption of ), #10.81, 11.56, 11.58, 11.59. It is possible that you already did these, since they were suggested for 2/17/09. If you have already written them out, you do not need to do them a second time. 2. Also due today: Group proposals and timelines for TSTTMP (Two-Sample t Test Mini-Project). Some ideas are listed below. IQ tests: How much learning effect is there if subject takes a second test with minor changes? Reaction time: In a Whac-a-Mole game, what is the mean effect of noise or other distractions? Driving performance: In a simulation game, what is the mean effect of text messaging or phoning? Multitasking: Does the mean time to write a paragraph increase when subject does other things at the same time? Choose one of these project ideas, or your group can make up a new one!
W 2/25/09	HW due: Write #11.60, 11.62, 11.63. Use the PHASTPC format for #11.63c.
Th 2/26/09	HW due: Revised group proposal with timeline and power analysis for sample size determination.
F 2/27/09	HW due: NMAP assignment.

Return to the STAtistics Zone

Return to Mr. Hansen’s home page

Return to Mathematics Department home page

Return to St. Albans home page

Last updated: 02 Mar 2009