|
M 12/1/08
|
Classes resume.
HW due: Read pp. 385-406, including all of the examples (Example 7.5 on p.
385, Examples 7.6 and 7.7 on p. 387, etc.) but omitting the exercises for
now.
|
|
|
T 12/2/08
|
HW due: Write #7.42abc. Show your work, and use
correct notation. Part (c) is not in the textbook but is shown below.
(c) If the measurements are normally distributed (a reasonable assumption),
compute P(X > Y). Show a
sketch, and explicitly define your supplementary variable, if any.
|
|
|
W 12/3/08
|
Quiz (10
pts.) on yesterday’s “Quick
Study” article. This is the last
quiz of this type for the school year.
HW due: Read pp. 415-423; write #7.34, 7.35, 7.43, 7.44abc, 8.38, 8.39.
|
|
|
Th 12/4/08
|
HW due: Read pp. 424-433; write #8.10, 8.22, and
finish any unfinished problems from yesterday’s assignment.
|
|
|
F 12/5/08
|
HW due: Read pp. 434-447.
|
|
|
M 12/8/08
|
HW due: Write out solutions for the following
questions. Adequate work is required in each case. Define the random variable being used, and state its distribution.
Use correct notation for all your answers. For example, a binomial random
variable may have the B(25,0.15)
distribution, and a geometric random variable may have the G(0.15) distribution.
1. Mr. Hansen’s brother is a much better free-throw shooter than Mr. Hansen,
sinking about 75% of his shots. Compute the probability that Mr. Hansen’s
brother sinks his first free throw in (a) fewer than 4 tries, (b) more than 4
tries, (c) on the first or second try. Then compute (d) the expected number
of successes in 18 tries and (e) the probability of more than 12 but fewer
than 15 successes in 18 tries.
2. The incidence of AIDS in a large city is 1.2%. An SRS of 1000 residents is
selected. Explain (a) why the binomial distribution for the number of
AIDS-afflicted people in the sample is not
correct but is nevertheless close enough for estimation purposes, and compute
(b) the expected number of AIDS-afflicted people in the SRS, (c, d) the
standard deviation and variance of that random variable, and (e) the expected
number of people drawn from the SRS before the first AIDS-afflicted person is
found.
3. The probability of a full house on the deal in 5-card draw poker is
3744/2598960, as we computed in class some weeks ago. If a woman plays this
game every week for 20 years, with 12 hands each time, compute (a) the
expected number of full houses on the deal she will receive, (b) the standard
deviation of that random variable, (c) the probability of receiving exactly
16 full houses on the deal, and (d) the probability that the number of full
houses on the deal is 13, 14, 15, 16, 17, 18, 19, or 20. When answering (d),
try to find a time-efficient way to compute the answer.
|
|
|
T 12/9/08
|
Test #6
(100 points, cumulative through Chapter 8).
|
|
|
W 12/10/08
|
HW due: Prepare a methodology statement
(approximately half a page, depending on how large you write) for the next
group project, which will be an experiment.
If you cannot think of anything interesting to run an experiment on, then you
may wish to write (as a permitted alternate assignment) a careful methodology
statement for the selection of groups. There are several requirements to keep
in mind. First, everyone should have at least one new coworker in his group,
i.e., someone with whom he has not already shared group membership this year.
Second, nobody should be a group leader if he has already served as a group
leader. There were 4 group leaders for the first project and 3 for the second
(after a group was disbanded), leaving 4 eligible people for this round: Ted,
Charlie, Sam, and Doug. Third, groups must have sizes 3, 3, 3, and 2. You may
wish to incorporate additional requirements as well.
|
|
|
Th 12/11/08
|
HW due: Prepare an original methodology statement
for a proposed experiment, showing blocking. Content will be graded. Indicate
how your design incorporates the principles of control, randomization, and
replication. (List a bullet item for each of those goals.)
In class: We will use Eddie’s selection methodology, as modified by Charlie,
in order to choose groups.
|
|
|
F 12/12/08
|
HW due: Meet as a group (or confer by telephone or
IM as needed) to decide upon an experiment to pursue, and prepare a written
project proposal. You may use one of the experiment concepts discussed in class,
or you may choose a new one and give a summary. For full credit, you must
include the following components:
- Research question, phrased as a question
- Brief summary of methodology , not a fully
detailed description (can be omitted if your group uses one of the
already submitted methodology statements with no significant changes)
- Blocking diagram (similar to the one given in
class on Wednesday, 12/10, except that only one level of blocking is
required)
- Milestone chart giving estimated dates for key
actions in your project, which may include some or all of the following:
methodology finalization, methodology approval, data gathering,
analysis, report writing, proofreading, draft submission, rewriting,
final assembly, and submission of hard copy.
Your proposal document must be in a hard copy
format. Handwriting is fine if your writing is legible.
For planning purposes, you should know that half of Monday’s class period and
nearly all of Tuesday’s class period will be reserved for group meetings. For
now, your milestone dates will serve as targets. The key deadline is 4:00
p.m. on January 6, but even that can be adjusted if you inform me with
adequate time to spare. (Extension requests submitted at the last moment will
not be approved. My rule of thumb is that the maximum time extension is the
time remaining until the deadline, on the theory that you should surely know
by x days in advance of the target
that you are running x or fewer
days behind schedule. For example, if you speak to me at 4:00 p.m. on January
5 to request an extension, the maximum amount of additional time you would be
granted is 24 hours, since only 24 hours remain until the published
deadline.)
Group 1: Charlie, Eddie, Patrick
Group 2: Sam, Jimmy, Stefan
Group 3: Doug, Ben, Grenville
Group 4: Ted, Cameron
|
|
|
M 12/15/08
|
HW due: Read top of p. 454 plus all of pp. 456-459,
and then rework last Tuesday’s test so that
it is 100% correct. Do not consult the answer
key until you have made a solid effort on each problem. (Otherwise, you
will not gain the maximum learning benefit.) All of these problems are fair
game for the upcoming midterm exam in January.
It is ideal if you can learn the material thoroughly before the test, but in the absence of that fortunate outcome,
learning after the test and before the exam is still valuable. Here are the
statistics from the test:
n = 11
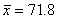
Q2 = 71
s = 12.2
IQR = 23
Typical values from my years of teaching are 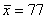 , s = 10. , s = 10.
In class: Mop-up operation on probability, experimental design, binomial and
geometric random variables. Remainder of period, approximately 25 minutes,
will be allocated to group work.
|
|
|
T 12/16/08
|
HW due: Read through p. 479, including all examples
(but not the exercises); write a definition of sampling distribution in your own words. Try to write your
definition without referring to your notes or to the textbook.
|
|
|
W 12/17/08
|
HW due: Read through p. 497. This is 12.5 pages of
reading after you subtract the exercises. Be sure to read the examples,
however. We will do exercises in class in order to maximize the time that you
have available to work on your project outside of class.
|
|
|
Th 12/18/08
|
No additional written work due. Please work on your
group project, and continue to bring all second quarter HW (since the
beginning of November) to class each day.
|
|
|
F 12/19/08
|
HW due: Solve the Statistics Mathcross (or at least
as well as you can). There is an interactive
version as well as a printable version.
You may use Google and Wikipedia to help you. A worthy attempt will qualify
for 4 points. You are exempt from this assignment if you check in with me at
the west end of the Cathedral as you leave Lessons and Carols on Thursday
night.
Note: Even chorale and orchestra
members need to check in with me to earn the exemption. I will be sitting too
far to the back to see people clearly.
|
|