|
M 11/3/08
|
HW due: Read pp. 286-296, including all 7 examples
(Example 5.17 on p. 287 through Example 5.23 on p. 294), but omitting the
exercises; write #5.64. Do not use randInt in part (b). Instead, use the following
rules applied to the random digit table on p. 836:
1. On your HW paper, write out your first, middle, and last names (legal
names). For example, Throckmorton Aloysius Gordon.
2. Count the letters in your first name, and multiply by 2. In our example,
the answer would be 24.
3. Count the letters in your middle and last names, and add that number to
the result from the previous step. In our example, the answer would be 14 +
24 = 38.
4. If the answer so far exceeds 50, add 50. Otherwise, add 100. In our
example, the final result would be 138.
5. Use the final result (in our example, 138) as the starting row for your
simulation. This is how Mr. Hansen will be able to check your answer.
|
|
|
T 11/4/08
|
HW due: Write #5.66, 5.68, 5.69, 5.73, 5.79, 5.81,
5.82. Please read additional comments for each problem in the notes below.
Notes:
- If you cannot finish all of these in one night,
do as many as you can and spread them out over two nights. It is
expected that everyone will do all 7 problems.
- In #5.66b, be sure to explain the difference
between male and female sample proportions. Propose several possible
explanations.
- In #5.68, a one-sentence answer is expected.
- In #5.69, the book’s answers are inadequate. Be
sure to describe a Monte Carlo protocol properly in part (a), and in
part (b), do not begin on row 105. Instead, use the row that you used
for Monday’s assignment (i.e., the row based on your legal name).
- In #5.73b, give your answers in the form of a
table.
- In #5.79, the book’s answers are inadequate and
do not include any explanations. You must show your simulation
(beginning on the same row you used for #5.69) and explain, through
clear arithmetic, why 2 is the optimal number of cheesecakes to produce.
Note that in some cases, the answer may not be 2, depending on how the
simulation works out.
- In #5.81, use any row other than row 120.
Record what row number you are beginning your simulation with, and
record the raw data of your simulation in a table.
- In #5.82, use a format similar to #5.81.
In class: Review HW, prepare for test.
|
|
|
W 11/5/08
|
At the request of the STA administration, the test
originally scheduled for today has been postponed one day. Also, please note
that there is no additional HW due today, so that you can follow the election
returns.
This is a historic election, and the science of statistics will be front and
center. This is our moment in the sun!
In class: Additional review.
|
|
|
Th 11/6/08
|
Test #4
(100 points, cumulative through Chapter 5).
Recently discussed terms you are responsible for would include the following:
sharpshooter fallacy
bias (data-snooping bias, confirmation bias, wording-of-the-question bias,
response bias, nonresponse bias, voluntary response bias, lack of realism,
Hawthorne effect/unintended feedback, selection bias, undercoverage,
overcoverage, placebo effect, COI, experimenter bias, hidden bias, etc.)
unbiased estimator
statistical significance
Monte Carlo method
simulation
sample proportion
control group
experiment
observational study
control (in experimental design)
randomization (in experimental design)
replication (in experimental design)
SRS (simple random sample)
stratified random sample
block design
matched pairs, matched triples, matched quadruples, etc.
event
success
trial (iteration)
Type I error (a.k.a. false positive)
Type II error (a.k.a. false negative)
|
|
|
F 11/7/08
|
No school.
|
|
|
M 11/10/08
|
HW due: Read the Quick
Study from last week and the Chapter Review on pp. 298-300 if you have
not already done so; read pp. 310-329. Skip Activity 6 (pp. 311-312) and the
exercises, but read all of the examples.
One or two open-note quizzes (one on the Quick Study, one on the reading
assignment) are possible.
|
|
|
T 11/11/08
|
HW due: Read pp. 331-334; write #6.18, 6.22. For
6.22, use a Venn diagram.
|
|
|
W 11/12/08
|
HW due: Read pp. 334-337, 341-344, 346-349; write #6.33,
6.35, 6.36. We will skip the Quick Study quiz this week, because I could not
locate the link.
|
|
|
Th 11/13/08
|
HW due: Read pp. 351-355 and the summary on p. 359;
write #6.54 and the following problem. (Hint:
A tree diagram is expected.)
Screening problem: Plastofibromystiblosis (a fictitious deadly disease) has
an incidence of 1.8% in the population of a large city. By law, a screening
test must be administered to every resident. The test is extremely accurate.
The probability of a positive test result, given that a person is infected
with the disease, is .98. (We call this the sensitivity of the test.) The probability of a negative test
result, given that a person is not infected with the disease, is even higher,
namely .985. (We call this the specificity
of the test.) Compute the probability that a person is actually infected with
plastofibromystiblosis, given that he or she has received a positive test
result. (This is what we call the positive
predictive value of the test.)
To summarize:
Sensitivity = P(+
| infected) = .98
Specificity = P(–
| ~infected) = .985
PPV = P(infected
| +) = _____________ (medium difficulty to compute this with a tree diagram)
|
|
|
F 11/14/08
|
HW due: Write #6.62, 6.64, 6.66, and repeat yesterday’s
plastofibromystiblosis problem with a small change that makes the problem
much easier (conceptually, at least). At the top of the tree, write “100,000
people” to represent a large pool of random subjects. Then, instead of
entering probabilities in the tree, enter the number of people that would be
expected to fall into each of the bins. You may find this example (using a different number of people)
to be helpful. Feel free to use whichever approach you prefer when you work
through #6.66.
|
|
|
M 11/17/08
|
HW due:
1. Take the conditional probability quiz.
In your paper, write each question and its correct answer (not simply the
letter of the correct answer, but the entire answer). Then, explain not only
why the correct answer is correct but why each of the plausible distractor
answers is incorrect. See the example below.
Example response for #1.
1. Events A and B are independent if and only if
(A) 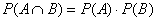
CORRECT based on class notes
from Thurs. 11/13/08.
(B) P(A | B) = P(A) P(B | A)
INCORRECT: This formula is a
corrupted version of the similar-looking formula
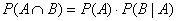 , which cannot in any event be used as a test for , which cannot in any event be used as a test for
independence. The latter
formula is always true, even if A and B and not independent.
(C) P(B | A) = P(A) P(B | A)
INCORRECT: This formula is a
corrupted version of the already corrupt answer in (B).
(D) None of the above.
INCORRECT: This choice is
designed to trap students whose metaknowledge is weak.
2. After you have completed the quiz and its associated writeup, fill out the
A
Priori Problem Set from last year. (Please ignore the due date on
that handout.)
3. Bonus question (optional): Two
cards are drawn without replacement from a well-shuffled standard 52-card
deck. Compute (a) the probability that the second card is an ace, given that
the first card is not an ace, and (b) the probability that the second card is
an ace, given that the first card is not a king.
|
|
|
T 11/18/08
|
HW due: All HW due yesterday will be scanned again,
with the addition that the bonus question is now required, along with the design
of a Monte Carlo simulation (using a random digit table) to see if your
answer is correct. You do not need to execute the Monte Carlo simulation, but
simply write out the design in detail.
|
|
|
W 11/19/08
|
HW due:
1. Prepare for the Quick Study quiz on this
article.
2. Prepare a list of at least 3 good test questions that would challenge you.
If yesterday’s pop quiz stumped you, you may want to include a problem or two
from that quiz, but most people would want to find more challenging
questions, either by recycling previously assigned homework or by making
problems that are similar in spirit to existing homework problems.
3. For each of your 3 questions, state exactly
where your difficulty or challenge lies. Do not say, “I don’t understand how
to do problems of this type.” Do say something specific, such as, “I don’t
understand why the general addition formula cannot be applied here. Is this not
a union?”
4. Be sure you have completed all previously assigned HW, especially the A
Priori Problem Set, since all those problems have been covered in
class.
After class: Check your mailbox to pick up your previous test. Statistics
were as follows: sample mean 82.9, sample s.d. 9.5. A comment regarding the
final question: While it is true that the HappyCal z-score is slightly
higher, this difference is not significant. The real issue is that HappyCal
students are drawn from a more selective pool than the SATM population.
(Essentially anyone with a pulse who lives in the U.S., other than the
Midwest, will take the SATM if he or she has any notion of attending
college.) Therefore, the HappyCal score is much more impressive.
|
|
|
Th 11/20/08
|
Test #5
(100 points, cumulative through Chapter 6). If you e-mail me your questions
(limit of 3 per student, please), I will be happy to provide assistance as
you prepare for this test.
|
|
|
F 11/21/08
|
No additional HW due. Please use this as an
opportunity to make sure that all previously assigned work is complete. Some
of the assignments, even fairly old ones, may be rescanned today. (You may
safely recycle your first quarter HW if you wish, however. That will lighten
your load slightly.)
|
|
|
M 11/24/08
|
HW due: Read pp. 367-380; write #7.8, 7.10.
|
|
|
T 11/25/08
|
Last day before Thanksgiving break; no additional HW
due.
In class: Guest speaker, Mr. Joe Morris (STA ’62) from MITRE Corporation. Before
Mr. Morris’s presentation, there may be a quiz and/or a HW scan for previous
assignments.
|
|
|
W 11/26/08
|
No school (Thanksgiving break).
|
|