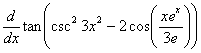Honors AP Calculus / Mr. Hansen 10/17/2008

Name: _________________________

Retest through §4-6 (Calculator Required)

Part I	Each correct answer is worth 4 points. Unlike the scoring on the AP exam, there is no penalty today for wrong guesses (other than the loss of the 4 points, of course.) Write the capital letter of the best choice in the blank provided. There is no partial credit. Points may be deducted if you circle or blacken your answer choices. If you wish to cross out distractor answers lightly, you may do so. Dark marks are not permitted.
___ 1.	All second-order “diffy q’s” where the independent variable is t and the dependent variable is P must involve at least one term equal to
	(A) a square of dP/dt (B) an expression involving dP/dt (C) a power of dP/dt (not necessarily squaring)	(D) d^2P/dt^2 by itself (no other operations) (E) an expression involving d^2P/dt^2
___ 2.	If f is a one-to-one function defined on Â, then f ^–1 must be
	(A) continuous (B) invertible (C) differentiable	(D) all of the above (E) both (A) and (B)
___ 3.	A student is asked to find the particular solution to a differential equation subject to several initial conditions. The student writes his answer as a number and circles it. Why does Mr. Hansen give no credit?
	(A) The number must have been wrong. (B) It is impossible to have more than one initial condition. (C) The student must have rounded his answer improperly. (D) The student should have written an expression involving variable(s), not a number. (E) The student should have written an equation involving variable(s), not a number.
___ 4.
	(A) (B) (C)	(D) (E)

___ 5.
	(A)	(D)
	(B)	(E) none of these
	(C)
___ 6.	The derivative can be defined as
	(A) the limit of the tangent slopes (B) the limit of the secant slopes (C) the average rate of change of a function	(D) division by zero (E) division by a tiny number h, e.g., .0001
___ 7.	If f '(x) < 0 for all real values of x, and if the range of f is Â, and if g(x) = f ^–1(x), then which of the following must be true?
	(A) g(x) is decreasing for all real x (B) g(x) is increasing for all real x (C) g(x) is continuous for all real x	(D) all of the above (E) only (A) and (C)
Part II	(12 pts. for each numbered problem)
8.	Make a table of values for x, f (x), and f ' (x). Pose and solve a multiple-choice problem related to the calculation of g ' at a certain value of x, where g = f ^–1. Make your problem challenging enough to reveal that you know what you are doing, and make sure that the probability of RAWR (right answer for the wrong reason) is low.

9.	Given: $x P(x), where P(x) is defined to mean that x is a plorg.
	Form the negation of the given statement, using the symbol " at some point: _______________________________________ State this negation in English (no symbols): ___________________________________________________________________
10.	Prove that for any atomic statements A, B, and C, ~(A Ù (B Ú C)) Û ~A Ú (~B Ù ~C). Hint: Your truth table should have 8 rows.
11.	Use your calculator to compute at the point x = 0.8. Answer: ______
	Then evaluate the derivative (retaining the x) using the rules we learned: Answer: _______________________________________________________________
	Plug x = 0.8 into this expression. What do you obtain? _________________________
12.	A laser beam centered at the origin is tracking a B-list celebrity (indicated by point B) who is walking eastward along a straight moving sidewalk. The speed of the moving sidewalk is 3 ft./sec., and the B-list celebrity is walking in the same direction as the motion of the sidewalk, at a fast walking pace of 4 ft./sec. relative to the sidewalk (not relative to the surrounding scenery). The sidewalk’s perpendicular distance from the origin is 30 ft. (a) Make a diagram and raise your hand so that your diagram can be verified. (b) Let x(t) denote the celebrity’s horizontal distance, left or right of the origin, at time t. Find dx/dt. (c) Compute the laser beam’s angular rate of change at the moment when x = 20 ft.

13.	Compute the following derivatives.
(a)
(b)