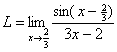Honors AP Calculus / Mr. Hansen

Name: _______________________________

9/16/2008

READ INSTRUCTIONS IN EACH PART! ______

 

Test #1 (100 points): Calculator permitted throughout

 

 

Part I: Multiple Choice (0 points off for a correct answer, –5 for an error, –4 for an omission).
Write the capital letter of the best choice in the blank provided. There is no partial credit, and work is ignored. Do not circle or black out anything. Points may be deducted if you do not follow instructions.

 

 

1. ___

For our purposes in HappyCal, a definition is . . .

 

 

 

 

(A)  an explanation of a term

(D)  the contrapositive of a theorem

 

(B)  a conditional statement

(E)  a formal system

 

(C)  a biconditional (“iff”) statement

 

 

 

2. ___

Chaos (in mathematics) is characterized by . . .

 

 

 

(A)  randomness

(D)  non-separability of differential equations

 

(B)  extreme sensitivity to initial conditions

(E)  robustness

 

(C)  separability of differential equations

 

 

 

3. ___

In the formal definition of , what is the reason for using a punctured -neighborhood of c in the clause that says 0 < | x – c | <  must imply | f (x) – L | < , instead of simply basing the definition on an open interval where x  (c – , c + )?

 

 

 

(A)  An open interval is not a neighborhood of a point.

 

(B)  There is no good reason; an open interval would work just as well as a punctured -neighborhood, but there is a tradition in calculus textbooks of using both  and  in the definition of limit.

 

(C)  The question is posed incorrectly. The formal definition of limit requires the function values to lie within a punctured -neighborhood of L, i.e., the set of y values such that 0 < | y – L | < , where y = f (x).

 

(D)  The question is posed incorrectly. The formal definition of limit requires the function values to lie within a punctured -neighborhood of L, i.e., the set of x values such that 0 < | x – L | < , where y = f (x).

 

(E)  We wish our definition to make no requirement that f (c) exists.

 

 

4. ___

Which of the following is true regarding the formal system we call “the calculus”?

 

 

 

(A)  It is never appropriate to have “jackets off” when studying the calculus.

 

(B)  Deep understanding and months of instruction are required in order to compute numeric answers.

 

(C)  Computers can obtain correct numeric answers to many problems.

 

(D)  The calculus is (mostly) a waste of time, since all important applications have now been formalized.

 

(E)   The two most important application areas rely exclusively upon the differential calculus, not the integral calculus.

 

 

5. ___

In Mr. Hansen’s opinion, the two most important application areas for students of the calculus are . . .

 

 

 

(A)  differential equations and variable-factor products

(D)  differential equations and mathematical pedagogy

 

(B)  chaos theory and marketing

(C)  textbook writing and hedge-fund management

(E)   public relations (p.r.) and variable-factor products

 

 

6. ___

If g(x) = x2 – 3, then  is defined as . . .

 

 

 

(A) 

(D) 

 

(B) 

(E) 

 

(C) 

 

 

 

7. ___

Real-world applications of differential equations include . . .

 

 

 

(A)  missile guidance

(D)  nuclear engineering

 

(B)  weather forecasting

(E)  all of these

 

(C)  modeling of fluid flow

 

 

 

 

Part II: Short Answer (5 points each, with essentially no partial credit).

 

No work is required or expected for #8 through #12. All numeric answers must either be exact or rounded to 3 decimal places. Be sure to hit MODE to place your calculator in radian mode.

 

 

8.

Let . Conjecture (do not prove) the value of L. Answer: L = ____

 

 

9.

Let , the expression whose limit, L, you found in #8. Find the largest 3-place value of  such that  implies f (x) is within 0.0015 units of L. Answer:  = ____

Note: If you could not compute L, raise your hand to forfeit credit for #8 and receive the value of L.

 

 

10.

State the formal definition of  for an arbitrary function f. You may use words, symbols, or a mixture.

 

 

 

______________________________________________________________________________

 

 

 

______________________________________________________________________________

 

 

11.

Use any method (MATH 8, etc.) to find  if g(x) = x2 – 3. Answer:  = ____

 

 

12.

Use any method (MATH 9, etc.) to find . Answer: ______

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Part III: Longer Answer (16 points each, partial credit available).

 

Show your work. Be neat and clear. The numeric answer, if any, is worth much less than the justification you provide. Complete sentences are not required.

 

 

13.

For the function g(x) = x2 – 3 used in #11 and #12, estimate the definite integral over [1.23, 2.57] by using the trapezoid rule with 4 intervals of width 0.335.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

14.

Prove, using great detail and justification(s) for each and every step, that  You may not use your calculator here. An “honors geometry” 2-column proof format is acceptable but is not required. Approximately 6 to 9 steps are required, depending on whether you do multiple changes in a single step or not. Please note that for full credit, “lim” must be written each time in the “quite sizzly” format, cursive preferred.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

15.

If we compute the definite integral of a velocity function (miles per hour) with respect to time (hours), what units will our answer be in? _______________ What does the answer mean in a real-world sense?

______________________________________________________________________________

______________________________________________________________________________

 

 

 

What gauge on a car displays the derivative (instantaneous rate of change) of the car’s displacement function? ___________________________

 

 

 

I have, in my car, an instantaneous mileage display that tells me, at any moment, the approximate fuel economy (in miles per gallon) that my car is achieving. In other words, this display is much like a speedometer, except that instead of telling me my instantaneous forward velocity in mph, it tells me my instantaneous fuel economy in mpg. If I am going downhill on the GW Parkway in Virginia, I can sometimes hit 80 or 90 mpg, but when I drive around in the Cathedral garage, I am lucky to achieve 5 mpg. An interesting thing to do might be to plot all these mpg readings (measured, say, every 0.1 mile) to make a graph. Since the mpg data represent instantaneous rates of change in my displacement per unit of fuel, these readings are (circle one) derivatives   average rates of change   definite integrals.

Now, just as I can take a definite integral of the car’s velocity function with respect to time, I might want to take a definite integral of the car’s mpg function with respect to distance as a way of determining my total fuel consumption. Since my readings are made only every 0.1 mile, my graph might well have some bumps and spikes in it, but I could certainly use the trapezoid rule or some comparable technique to estimate the definite integral. However, this does not work for computing total fuel consumption. Why not? (Hint: Think of the units.)

______________________________________________________________________________

______________________________________________________________________________

What function could I integrate with respect to distance as a way of determining the total amount of fuel consumed? (Hint: There is no gauge on my car that displays this function, at least not directly, but if I am ambitious enough to record data readings every 0.1 mile, I could certainly figure out a way to compute this function.)

______________________________________________________________________________

______________________________________________________________________________

______________________________________________________________________________